見積りは科学であり、ソフトウェア開発は不確実性との戦い
はじめに
イオンスマートテクノロジー株式会社(通称AST)のCTO室TechLeadチームの@t0doroki_takaです。
本記事の内容は、上記の書籍で紹介されている手法を自分の解釈で整理・アレンジしたものです。
計画段階から完成形を定義して、全体の開発工数・工期を見積もって年単位で開発を進めるプロダクトは、アジャイルという考え方の無かったウォーターフォール・モデル時代の考え方なのかもしれません。とはいえ、業務システム開発においては、プロジェクト開始直後からアジャイル開発することは難しく、このような見積もりは欠かせないと思います。
なぜなら、多くの業務システムは、出来る限り早く市場に投入してフィードバックを得てピボットする性質のサービスではなく、予め要件・機能を定義してステークホルダーとの合意形成が不可欠です。アジャイル的な開発を導入するにしても、事前に全体規模の把握は必要です。その際に必要となる見積もり方法に、先人の知見を活かさない手はありません。
不確実性と見積もり
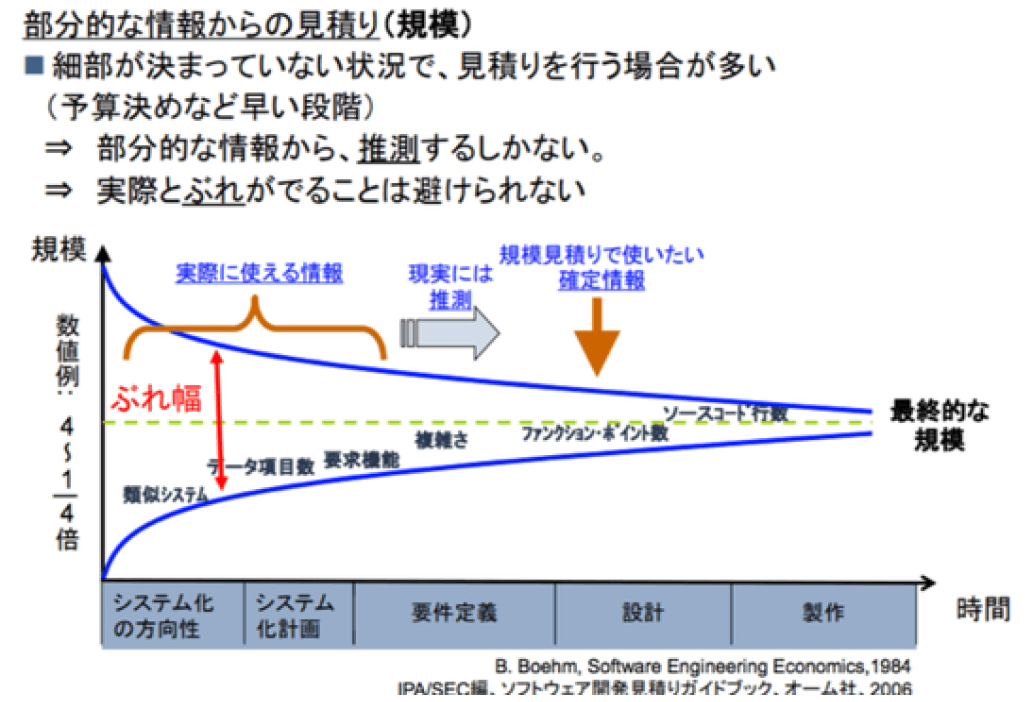
不確実性コーン
ソフトウェア開発は不確実性との戦い。
- 見積もりはブレる。誰にも正確な予測は不可能。
- 形式上ブレていない様に見せるためにバッファを積む。
- プロジェクト全体で巨大化。
- (もしくは、予算と納期ありきで絶対的に工期・工数足りない見積もりに・・)
- (進捗報告にて「リカバリープランは?」「増員で対応・・、休日に対応・・」など)
という悪循環。
見積もりと実稼働にブレが発生する最大の原因は不確実性。
- 何を作ったら良いのか分からない
- 不明瞭(曖昧な部分)
- 不明確(正確かどうか分からない部分)
- 「知らないと知らないこと」(unknown unknowns)の存在
- ある工程の完了ごとに、ある工程の不確実性をゼロには出来ない
- 要求、要件を事前に完全に定義することは不可能。
- 設計から要件定義へのフィードバックや質疑応答の発生などは避けられない。
これらのあらゆる不確定要素を(出来る限り)見える化して、見積もりに織り込む必要性あり。
- 不確定要素の見える化 & 見積もりへの織り込み
- 都度アップデートを行い、見積もりを段階的に精緻化
タスクとそれを完了するために必要な作業の全体像を視覚化するための、一つのアプローチとして、有名なPERTがある。PERTは、米国海軍のポラリス潜水艦発射弾道ミサイルシステム開発の工期を短縮したことで有名。
アローダイアグラムでプロジェクトの工期管理していく方法で、この中に三点見積りという工数推定方法がある。三点見積りとは、ベータ分布の近似工数を期待値、分散を推定していく方法。
また、タスクの繋がりをアローダイヤグラムで表現して、クリティカルパスを分析する。クリティカルパスは同時並行して進むタスクにおいて、最長工期を必要とするパス。同時期にデュポン社で開発されたクリティカルパス法に類似。
以降、三点見積りを要約する。クリティカルパスに関しては触れない。
三点見積り
一点見積もりは、不確実性に対応するためのバッファを積んでいくことにより、プロジェクト全体で肥大化する傾向があり、不確実性の把握とそれに対する見積もりを正確に反映していない。
三点見積りは、最良ケース、有力ケース、最悪ケースの三点で見積もりを行う。三点見積りでも、不確実性に対応するためのバッファを積む事には変わりないが、ベータ分布の近似工数を用いることで、バッファの最大値の合計よりも確率分布を元に現実的な判断をできるようにする。また、不確定要素を見える化して各ケースに反映する事で、リスク管理、見積もり根拠の明確化、見積もり精度の向上などを図る。

三点見積りと確率分布
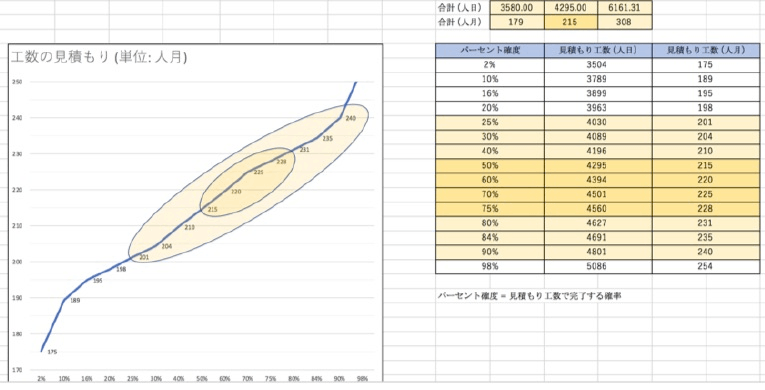
Y軸:工数, X軸:確率分布
各機能単位で算出した最良ケース、有力ケース、最悪ケースを合算した値を見積もり値として使用するのではなく、最良ケースと最悪ケースから算出した標準偏差を元に確率分布を算出する。
上記の表に基づいて確率分布(パーセント確度)を算出すると、上記の図では下記が読み取れる。
- 25%〜90%の確率で201〜240人月の間
- 50%〜75%の確率で214〜228人月の間
- 最悪ケースで308人月
最悪ケースの合計はレアケースであり現実的なものではない。リスク管理やマネージメントでの回避可能の範囲になる。
見積もりロジック
機能一覧で定義される各機能に対して、下記の見積もりを行う。
前提
- 機能一覧を階層化する。概ね 1 REST API に相当する粒度まで落とし込む(Lv.3程度)。
- それらを積み重ねる事で全体工数を把握する(WBS法に近い)。
- 各ドメイン領域、もしくは機能単位に対して不確定要素を洗い出しの必要性。
ケースの定義
- 最良ケース: 設計見積もり + 製造見積もり
- 有力ケース: 最良ケース + Σ(不確定要素)
- 最悪ケース: 有力ケース + Σ(見えていない不確定要素)
「製造見積もり」「不確定要素」「見えていない不確定要素」の考え方は後述。
手順
- 各機能単位ごとに上記の3ケースを見積もる。
- 総見積もり(機能合計)を、見積もり工数が一定の範囲に入る確率分布として算出する (=不確定要素と見積もりブレの可視化)。
- 見積もりの精緻化を継続的に行う。
見積もりの精緻化
見積もりの精緻化とは、不確定要素の見える化。
- 「見えていない不確定要素」を「見える不確定要素」にする。
- 仮説(「知らないと知らないこと」(unknown unknowns)を予測)
- 何を作ったら良いのか分からない部分を無くす。
- 不明瞭(曖昧な部分)
- 不明確(正確かどうか)
「不確実性 = 何を作ったら良いのか分からない」を無くしていく事で、設計・製造に直結する避けられないタスクであり、不確定要素の内容の明確化に連動して見積もりのブレ幅も減少していく。
不確定要素の定義
- 解決しないと(どこかで)先に進めなくなる事柄。
- 要件として落とし込まれているが、疑問点や不明瞭(曖昧な部分)・不明確(正確かどうか)な事柄。
- 何らかの外的要因で要件・仕様変更の必要性が発生する可能性のある事柄。
具体的に、ある機能を製造するのに何が不確定要素となるか? 例えば、REST APIを実装する場合、
- データベース物理設計
- REST API詳細設計
- 何かの値の算出方法
- 処理手順
これらの仕様確定の阻害、仕様変更の要因となるあらゆる事柄を不確定要素と定義する。
上記のREST APIを実装するのに必要な資料は下記の工程を経て作成されるが、それらの工程が未実施の場合は、それらの工程自体が不確定要素となる。
- 要求定義・要件定義
- 外部設計 (基本設計)
- 内部設計 (詳細設計)
また、これらの工程が完了、もしくはある程度進んでいたとしても、その中で疑問点や不明確な事項があれば、それらは全て不確定要素としてリストアップする。これらの工程を進めるに当たり、インプット情報が足りないという事柄もそれらの工程自体が不確定要素となる。ここで、インプット情報が足りているかどうかは、ある程度調査しないと分からないが、調査しないと分からないという事柄も不確定要素としてあつかう。
不確定要素の見える化
タスク化と見積もり用のメタ情報の付加。
- 阻害内容
- これを解決しないと何が進まなくなるのか
- 無視して続ける事は可能か? その場合はどこにどれだけの影響があるか
- 期待インプットは何か
- 期待インプットが提供されたとして、どこに影響するのか
- REST API仕様, データベース物理設計など…
- それ自体を解決する工数目安
- すでにある部分に対する修正工数
- 期待インプットは何をしたら作成できるのか
- どこに影響ある
- ・・・
全機能で確実に存在する不確定要素
- UIとのすり合わせ
- REST API仕様
- データベース物理設計
- 外部システム連携とのすり合わせ
- バッチ処理設計
- データベース物理設計
要件・仕様管理(ドメイン領域ごとに下記を作成。機能一覧の各機能との対応情報をマッピング)
- 要求一覧
- 業務フロー一覧
- 業務ルール定義一覧
- 不確定要素のリスト
見積もりのパラメータ・係数
機能一覧から機能単位(Lv.1)ごとに見積もり。
見積もり工数 = 標準工数 x 個数 x 係数
- 基準: 1-REST APIあたりの製造・試験に必要な標準工数(過去実績)を設定
- 個数: 想定されるREST APIの数 (一般的なCRUD操作は、一覧、詳細、登録、変更、削除の5つ)
- 係数: データモデルの複雑さ(テーブル数, カラム数, テーブル間の相関関係の複雑さ)
不確定要素の見積もり (有力ケースと最良ケースの差分)
「不確定要素」の見積もりは、見積もり確度50%程度で設定(バッファを盛りすぎない)。
- 概算見積もり: 1,2,3,5,8,.., フィボナッチ数列をタスク間の相対値として設定 (目安:1=1人週)
- 精緻化: 実工数として見積もり (目安:1人週単位)
見えていない不確定要素の見積もり (最悪ケースと有力ケースの差分)
「見えていない不確定要素」は、見えていないので見積もれない。そこで、不確定要素の工数見積もりに対する確度の調整に使用する。具体的には、見積もりが「最良ケース〜最悪ケース」の範囲に入る見積もり確度を98%にする補正値を選択。
- Σ(不確定要素) x 係数 を見えていない不確定要素の見積もりとして設定
- 係数: 1 (※ 暫定値)
標準偏差から計算した総見積もりのパーセント確度の算出方法
個々の機能に対して、下記を算出する。
- 最良ケース、有力ケース、最悪ケース、それぞれの見積もり
- 標準偏差、分散を算出
- 標準偏差 = (最悪ケース - 最良ケース) ÷ 6
- 分散 = (標準偏差の2乗)
その際、最良ケース〜最悪ケースの見積もり確度98%を想定する。別の言い方をすれば最悪ケースを超えるのは2%くらいの確率くらいの確度を想定して見積もる。
全機能に対して、下記を算出する。
- 最良ケース = 各機能の最良ケースの合計
- 有力ケース = 各機能の有力ケースの合計
- 最悪ケース = 各機能の最悪ケースの合計
- 分散 = 各機能分散の合計
- 標準偏差 = 分散の平方根
| パーセント確度 | 計算 |
|---|---|
| 40% | 有力ケースの合計 - (0.25 x 標準偏差) |
| 50% | 有力ケースの合計 |
| 60% | 有力ケースの合計 + (0.25 x 標準偏差) |
| 70% | 有力ケースの合計 + (0.52 x 標準偏差) |
| 75% | 有力ケースの合計 + (0.67 x 標準偏差) |
| 80% | 有力ケースの合計 + (0.84 x 標準偏差) |
| 84% | 有力ケースの合計 + (1 x 標準偏差) |
| 90% | 有力ケースの合計 + (1.28 x 標準偏差) |
| 98% | 有力ケースの合計 + (2 x 標準偏差) |
| 100% | 最悪ケースの合計 |
上記の表に沿ってパーセント確度を算出する。

上記の表に基づいて確率分布(パーセント確度)を算出すると、上記の図では下記が読み取れる。
- 25%〜90%の確率で201〜240人月の間
- 50%〜75%の確率で214〜228人月の間
- 最悪ケースで308人月
見積もり内容から取り得る工程パターン
- 製造 → 不確定要素の解決 → 仕様変更 → 改修
- 不確定要素の解決 → 仕様変更 → 製造
改修規模と製造着手時期や人員リソースなどのトレードオフの検討材料になる。
おわりに
私は、「アジャイル vs. ウォーターフォール」や、モダン、トラディショナルなど、何かを区別する必要はなく、自分たちのプロダクト/プロジェクトで取り入れる価値のあるものは取り入れたいと思っています。
トラディショナルな業務システム開発においてもアジャイルで培われたやり方も積極的にフィードバックしていく。その逆に、アジャイル的な開発においてもトラディショナルの良い点は積極的に導入していく。全ては手段であって、システム開発の苦労を最小限にする(しなくてよい苦労はしない)ための方法でしかありません。今後、私自身の過去の経験や考察、これからやってみたいアイデアなど、記事にしていきたいと思います。
絶賛採用中です!
イオンスマートテクノロジーではエンジニアをはじめとした様々な職種を積極的に採用中です!
これからとてもおもしろいフェーズへ突入していくと思いますので興味のある方は是非カジュアル面談などで話を聞いてください!
Discussion