✏️

【英数字パスワード vs 数字パスワード】強度の計算をしてみた（H27年情報セキュリティスペシャリスト試験午後Ⅱ問2解説）

2024/08/24に公開

Security

やること

英数字（62種類）x桁と、数字のみ(10種類)16桁のパスワードにおいて、英数字の方が強度が高くなるには、最低限、英数字は、何桁（x）必要なのかの計算を、H27年情報セキュリティスペシャリスト試験午後Ⅱ問2の問題を元に解説します。

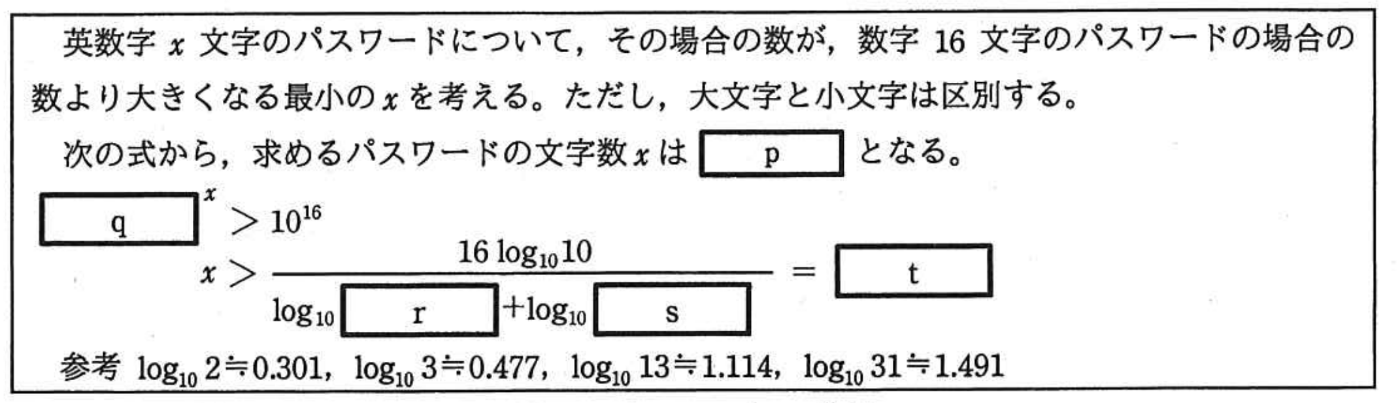
出典：IPA 2015年度秋　情報セキュリティスペシャリスト試験（SC）午後Ⅱ問2

パスワードの総数の計算

まず、それぞれのパスワードの組み合わせ総数を計算します。

英数字62文字のパスワード（長さ：x）
各文字には62通りの選択肢があります。
パスワード全体の総数は

62^x

です。

数字16文字のパスワード:
各文字には10通りの選択肢があります。
パスワード全体の総数は

10^{16}

方程式

英数字62文字のパスワード総数が、数字16文字のパスワード総数よりも大きくなる
x を求めます。
この条件を式で表すと:

62^x > 10^{16}

対数を使った計算

この不等式を解くために、両辺の対数を取ります。一般に、指数の不等式は対数を使って解くことができます。

\log(62^x)>\log(10^{16})

対数の性質により、上記の式は次のように変形されます。

x・\log(62)>16・\log(10)

次に両編をlog(62)で割ってxを求めます。

x > \frac{16・\log(10)} {log(62)}

さて、ここで、対数の性質を使って分母のlog(62)を次のように考えて計算します。

まず積の形で表現する

log(62) = log(2 * 32)

次にこの式は以下のように変形できます。

log(2 * 32) = log(2) + log(32)

以上をまとめると以下の式は、、

x > \frac{16・\log(10)} {log(62)}

このようになります。

x > \frac{16・\log(10)} {log(2)+log(32)}

ここで、問題文をみると、

$\log_{10} 2 ≒ 0.301$ $\log_{10} 31 ≒ 1.491$

と記載がありますね。
これは、計算で利用するから書いてあるに決まっている！ということでこれを使います。

分母 ： {log(2)+log(32)} ≒ 1.792

分子　：　　16・\log(10) ＝ 16

※log(10)は1のため、16 * 1 = 16
となり、

16\div1.792 ≒ 8.93

と計算することができます。

結果

桁数は整数である必要があり、その最小の数、つまり最低限何桁必要なのかは、9桁となります。

免責事項

情報の正確性について

当ブログでは、IT技術に関する情報や知識を提供していますが、その内容の正確性や信頼性については十分に注意を払っております。しかし、掲載されている情報が最新であるか、正確であるかについて保証するものではありません。また、予告なく内容を変更、修正、削除する場合があります。ブログの情報を利用する際は、必ずご自身の責任で行ってください。
法律的助言について

当ブログで提供している情報は、一般的な情報提供を目的としており、法律的な助言を提供するものではありません。具体的な法律問題や個別の案件については、弁護士などの専門家に相談されることをお勧めします。
外部リンクについて

当ブログでは、参考資料や関連情報として外部のウェブサイトへのリンクを提供することがありますが、これらのリンク先サイトの内容や安全性については責任を負いかねます。リンク先サイトの利用に関するトラブルや損害については、リンク先の運営者の責任となりますので、ご了承ください。
免責事項の変更について

当ブログは、予告なく本免責事項の内容を変更することがあります。変更後の免責事項は、当ブログに掲載された時点で効力を生じるものとします。最新の内容をご確認いただくことをお勧めします。