👻
Kinect Fusionで作る3Dスキャナその２

おおひら
2025/11/18に公開
Unity
tech
 前回のおさらい前回の記事では、センサーから取得した深度画像をもとに点群と法線を計算し、ICPを用いて各フレームのカメラ姿勢を推定する方法を紹介しました。
今回は、このカメラ姿勢情報を活用して、TSDFボリュームへの統合とレイキャスティングによる表面再構築の仕組みを解説していきます。

 6. TSDF（Truncated Signed Distance Function）
 6.1 TSDFとは何か？ここまでで、カメラの位置（姿勢）はICPで求まりました。
では、そのカメラから見た深度画像をどうやって1つの3Dモデルに統合するのでしょうか。
Kinect Fusionでは、 TSDF（Truncated Signed Distance Function） という方法で実現しています。
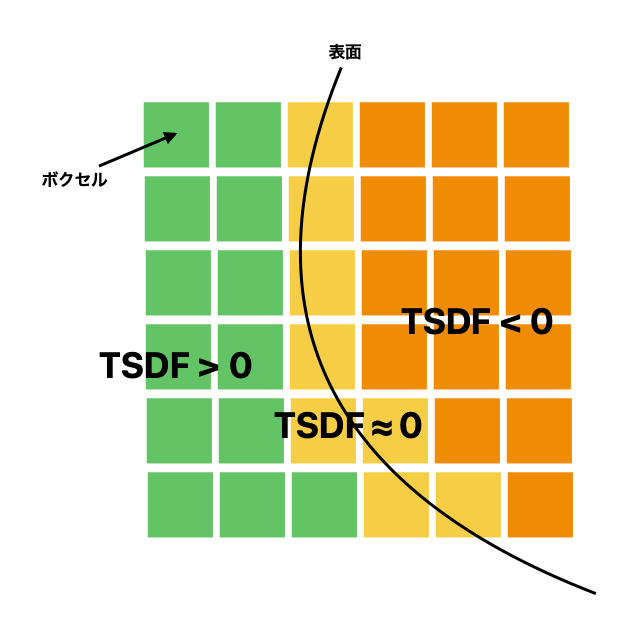
簡単に言えば、TSDFは「空間中の各点が、物体表面からどれだけ離れているか」を記録する仕組みです。
距離には符号があり、
表面の外側 → 正の値
表面の内側 → 負の値
ちょうど表面上 → 0
というルールで表現します。
ただし、すべての空間に距離を記録することは不可能なため、

一定範囲（truncation距離 δ）内の値だけを扱います。これが「Truncated」の意味です。


TSDF(x) =
\begin{cases}
\frac{sdf(x)}{\delta} & \text{if } |sdf(x)| < \delta \\
\text{未定義} & \text{otherwise}
\end{cases}

ここでの sdf(x) は、点 x と実際の表面との符号付き距離です。
このようにして、表面の近くの領域だけを滑らかに表現できるのがTSDFの特徴です。

 6.2 ボクセルグリッドの構造を理解するTSDFは3D空間を小さな立方体（ボクセル）に分けて管理します。

1つ1つのボクセルが、「ボクセルの位置におけるTSDF値」と「重み」を保持しています。
たとえば、512×512×512のグリッドを想像してみてください。

これは1辺が512ボクセルの立方体で、各ボクセルが1つのTSDF値を持っています。
このグリッドはワールド座標系で固定され、

各フレームのカメラ姿勢が変化するたびに、その視点から見た深度画像によって更新されます。

 6.3 TSDFの更新（ボリューメトリック統合）Kinect Fusionでは、新しい深度画像が得られるたびに、各ボクセルのTSDF値を次の式で更新します。


TSDF_{new} = \frac{W_{old} \cdot TSDF_{old} + tsdf_{obs}}{W_{old} + 1}



W_{new} = \min(W_{max}, W_{old} + 1)

ここで


TSDF_{old}：過去フレームまでの統合結果 \\

tsdf_{obs}：今回の観測に基づくTSDF値 \\

W_{old}：これまでの観測回数（重み） \\

W_{max}：重みの上限（通常 100〜200 程度）

つまり、過去の観測と今回の観測を「重み付き平均」で融合しています。

こうすることで、ノイズの多い深度値を少しずつならしながら、より安定したモデルを構築できます。
実装イメージは以下の通りです。
void updateTSDF(int voxel_index, float tsdf_obs)
{
    float W_new = voxel[voxel_index].W + 1;
    voxel[voxel_index].TSDF = (voxel[voxel_index].W * voxel[voxel_index].TSDF + tsdf_obs) / W_new;
    voxel[voxel_index].W = min(W_max, W_new);
}

 6.4 TSDF値の観測からの算出では、新しい深度画像から tsdf_obs をどう求めるのかを見てみましょう。
各ボクセル中心をカメラ座標系に変換
その点を画像平面に投影し、ピクセル座標 (u, v) を取得
深度画像上の観測深度 d_{obs} を読み取る
そのボクセルの投影深度 d_{proj}（カメラからの距離）との差を取る

sdf = d_{obs} - d_{proj}
もし |sdf| < \delta なら正規化して tsdf_{obs} = \frac{sdf}{\delta} とする。
こうして、カメラが動きながら深度画像を統合していくと、

ボクセルグリッドのTSDF値が少しずつ表面の形状を反映していきます。

最終的には、TSDF = 0 の等値面を抽出することで、3Dモデル（メッシュ）を得ることができます。

 7. レイキャスティングで表面を取り出す
 7.1 なぜレイキャスティングが必要かTSDFの中には、あくまで「距離関数」の情報しか入っていません。

そのままではメッシュ（表面）として見えません。

そこで、レイキャスティング（Ray Casting） を使って「表面＝TSDF=0の位置」を取り出します。
これは、各ピクセルから光線を飛ばし、TSDFが正から負に変わる点（ゼロ交差）を探す手法です。

 7.2 表面検出の基本アルゴリズム1本のレイに沿って、TSDF値を一定間隔でサンプリングします。
もし前回のサンプルが正、今回のサンプルが負であれば、その間に「表面＝TSDF=0の位置」があります。
次のように、線形補間で交点を求めることができます。

t_{zero} = t_{prev} + \frac{tsdf_{prev}}{tsdf_{prev} - tsdf_{curr}} \cdot (t_{curr} - t_{prev})
実装イメージは以下の通りです。
float3 Raycast(float3 ray_origin, float3 ray_dir, float t_min, float t_max, float step)
{
    float tsdf_prev = 0.0f;
    bool has_prev = false;

    for (float t = t_min; t <= t_max; t += step)
    {
        float3 pos = ray_origin + t * ray_dir;

        // トリリニア補間によるサンプル (詳細は後述)
        float tsdf_curr = TrilinearSampleTSDF(pos);

        if (has_prev)
        {
            // 符号が反転したらゼロ交差
            if (tsdf_prev > 0.0f && tsdf_curr < 0.0f)
            {
                // 線形補間でゼロ交差位置を求める
                float alpha = tsdf_prev / (tsdf_prev - tsdf_curr);
                float t_zero = t - step * (1.0f - alpha);
                return ray_origin + t_zero * ray_dir;
            }
        }

        tsdf_prev = tsdf_curr;
        has_prev = true;
    }

    // 表面が見つからなかった場合
    return (float3){Nan, Nan, Nan};
}
このようにして、各ピクセルごとに1つの交点（=再構築された表面上の点） を求めます。
ちなみに、この表面点群（頂点マップ、法線マップ）は次のフレームでのICPステップでモデル表面として利用されます。

 7.3 トリリニア補間によるサンプリングTSDF値はボクセルグリッド上の格子点で定義されています。

しかし、レイはその間を通るため、格子点以外の座標におけるTSDF値が必要になります。
そこで用いるのが トリリニア補間 です。

これは、近傍の8つのボクセル値を距離に応じて重み付け平均することで、

中間点のTSDF値を滑らかに推定する手法です。
実装イメージは以下の通りです
float TrilinearSampleTSDF(
    float3 p    // サンプリングしたい点（ワールド座標系）
)
{
    // ワールド座標 => ボクセル座標への変換
    float3 local = (p - voxel_origin) / voxelSize;

    // 参照ボクセルのインデックス
    int x = (int)floor(local.x);
    int y = (int)floor(local.y);
    int z = (int)floor(local.z);

    // ボクセル内のオフセット
    float fx = local.x - x;
    float fy = local.y - y;
    float fz = local.z - z;

    // 周囲8セルのTSDF値を取得
    float c000 = voxel[GetVoxelIndex(int3(x,     y,     z))].TSDF;
    float c100 = voxel[GetVoxelIndex(int3(x + 1, y,     z))].TSDF;
    float c010 = voxel[GetVoxelIndex(int3(x,     y + 1, z))].TSDF;
    float c110 = voxel[GetVoxelIndex(int3(x + 1, y + 1, z))].TSDF;
    float c001 = voxel[GetVoxelIndex(int3(x,     y,     z + 1))].TSDF;
    float c101 = voxel[GetVoxelIndex(int3(x + 1, y,     z + 1))].TSDF;
    float c011 = voxel[GetVoxelIndex(int3(x,     y + 1, z + 1))].TSDF;
    float c111 = voxel[GetVoxelIndex(int3(x + 1, y + 1, z + 1))].TSDF;

    // X方向の補間
    float c00 = lerp(c000, c100, fx);  // (y,z)
    float c10 = lerp(c010, c110, fx);  // (y+1,z)
    float c01 = lerp(c001, c101, fx);  // (y,z+1)
    float c11 = lerp(c011, c111, fx);  // (y+1,z+1)

    // Y方向の補間
    // z平面ごとにy軸方向を補間
    float c0 = lerp(c00, c10, fy);  // z
    float c1 = lerp(c01, c11, fy);  // z+1

    // Z方向の補間
    // 最後にz軸方向で補間
    float tsdf_value = lerp(c0, c1, fz);

    return tsdf_value;
}

 7.4 法線ベクトルの推定表面点がレイキャスティングで求まったら、次は法線（向き）を求めます。
法線は、表面の「向き」を示すベクトルで、TSDFの値が変化する方向と一致します。
言い換えると、法線はTSDFの勾配ベクトルを正規化したものです。

\mathbf{n} = \nabla TSDF =
\left[
\frac{\partial TSDF}{\partial x},
\frac{\partial TSDF}{\partial y},
\frac{\partial TSDF}{\partial z}
\right] \\

\mathbf{n} = \mathbf{n} / ||\mathbf{n}|| (正規化)
この偏微分を実装する際は、周囲のボクセルとの差分から近似的に求めます。
例えば、x方向の勾配は

\frac{\partial TSDF}{\partial x} \approx \frac{TSDF(x+\delta, y, z) - TSDF(x-\delta, y, z)}{2\delta}
実装イメージは以下の通りです
float3 ComputeGradient(
    float3 p    // 法線を求めたい表面点（ワールド座標）
)
{
    float delta = voxelSize; // ボクセルサイズを基準に中心差分を計算

    // 中心差分による各軸方向の勾配
    float dx = TrilinearSampleTSDF(p + float3(delta, 0, 0)) - TrilinearSampleTSDF(p - float3(delta, 0, 0));
    float dy = TrilinearSampleTSDF(p + float3(0, delta, 0)) - TrilinearSampleTSDF(p - float3(0, delta, 0));
    float dz = TrilinearSampleTSDF(p + float3(0, 0, delta)) - TrilinearSampleTSDF(p - float3(0, 0, delta));

    float3 grad = float3(dx, dy, dz);

    // 正規化して返す
    return normalize(grad);
}

 最後に本稿では、Kinect Fusion の全体アーキテクチャを順に追いながら、各処理ステップの概要と実装上のポイントを紹介しました。
深度画像取得と点群生成

　センサーから取得した深度画像を使って、各画素の3D座標と法線を計算
カメラトラッキング（ICP）

　前フレームとの差分からカメラの動きを推定し、各フレームのカメラ姿勢を計算
TSDF ボリューム統合

　各フレームの点群をボリュームに統合することで、メッシュを構築できるようにする
レイキャスティングによる表面再構築

　TSDF ボリュームから表面を抽出してメッシュを生成し、次フレームのICPに利用
このように、Kinect Fusion は連続的な深度画像オンリーで3Dモデルを生成できる強力な手法です。

 付録：補足事項ここでは、本稿では説明できなかった内容について補足します。
ICPの最適化パラメータから姿勢行列への変換処理
ICPの最適化では、更新パラメータは線形空間（Lie代数）上で導出されます。

その後、実際の姿勢行列を得るためには、指数写像によって非線形空間（Lie群）に変換するのが数学的に正しい手順です。
しかし、提供しているリポジトリではこの変換を省略し、オイラー角を用いて直接姿勢行列を導出しています。
数値的安定性に関しては、厳密なLie群ベースの方法とオイラー角による直接変換のどちらが優れているかについて、十分な検証ができていないため、本稿では結論を控えます。
マーチングキューブについて
マーチングキューブは、Kinect Fusionのアーキテクチャに含まれませんが、最終的にボクセルグリッド全体からメッシュを構築する際に使用されます。
レイキャスティングで表面点を取り出す場合と異なり、マーチングキューブはボクセル単位でTSDFのゼロ交差を探索して三角形メッシュを生成します。
比較：
レイキャスト：各ピクセル方向に沿って1点を探索
マーチングキューブ：各ボクセルの周囲8頂点をチェックし、ゼロ交差に応じて三角形を生成
細かい実装上の違い（エッジ補間や法線の計算など）はありますが、基本原理は同じくゼロ交差を利用する点です。
TSDFボクセルグリッドのメモリ効率
TSDFボリュームは、例えば 512×512×512 のフルグリッドだと非常に大きなメモリを消費します。
対策として、TSDFと重みの精度を下げる方法があります。
Kinect Fusionでは、float（32bit）ではなくhalf（16bit）を使用することで、使用メモリを半分にして最適化する工夫がなされています。
struct Voxel
{
    // TSDF
    public half tsdf;
    // TSDF integration weights
    public half weight;
}
GPU実装（Unity Compute Shader）
本稿で提示した疑似コードを愚直にCPUで実装すると、１フレームあたり数十秒程度かかる場合もあります。
実際のKinect Fusionでは高速化のため GPU を使用します。
本稿のリポジトリではUnityのCompute Shaderを用いて、各ステップを並列処理することで大幅な高速化を行なっています。
今回は詳細を省略していますが、今後の技術ブログでCompute Shaderによる最適化手法や実装上の注意点 について詳しく紹介する予定です。
株式会社アビストイノベーションセンターPublication
前回のおさらい

6. TSDF（Truncated Signed Distance Function）

6.1 TSDFとは何か？

6.2 ボクセルグリッドの構造を理解する

6.3 TSDFの更新（ボリューメトリック統合）

6.4 TSDF値の観測からの算出

7. レイキャスティングで表面を取り出す

7.1 なぜレイキャスティングが必要か

7.2 表面検出の基本アルゴリズム

7.3 トリリニア補間によるサンプリング

7.4 法線ベクトルの推定

最後に

付録：補足事項

Discussion
