有限要素法(FEM)を体験しよう
はじめに
有限要素法は、解析的に解くことが難しい微分方程式の近似解を数値的に解くことができる手法です。有限要素法は身近な例として、自動車の衝突シミュレーションや、橋が重さや振動によって破損しないかの検証などにも使わています。
本稿は、機械や建築の人がよく使う有限要素法(FEM: Finite Element Method)って何?と思ってる方に向けて書いています。
有限要素法って何?
有限要素法とは数値解析法の一種です。解析対象を多数の要素に分割し、それぞれの要素に対して節点ごとに求めたい解を導出します。そして、導出したそれぞれの解を足し合わせることで最終的な解を得る手法です。

Fig.
つまり、どのような挙動をするか予測困難で複雑な形状・性質を持つ物体があるとします。全体の挙動を一度に知ることはできませんが、物体をきわめて細かく分割したら、分割した一つ一つの挙動は求めることが出来る。じゃあその細かく分割した要素一つ一つに対して挙動を求めていき、最後に足し合わせたら全体の挙動が分かるじゃないか!という考えが有限要素法です。
目的
本稿の目的は、今から説明するプログラムを読者に実際に実行してもらうことで有限要素法に対するイメージや便利さを理解してもらうことです。
したがって、有限要素法の内部処理のイメージや、記載されているプログラムを使ってもらうための説明に重点をおいています。
有限要素法の中でも代表的である弾性有限要素法について説明していきます。弾性有限要素法とは、物体に力を加えたときの変形のようすを求める手法です。有限要素法内にでてくる式の詳しい意味や成り立ちは、参考文献
本記事を理解するとできること
本記事を理解することで、直方体に荷重を加えた時の変位を求めることができます。直方体の形状や荷重および拘束をかける場所は任意に変更できます。
例えば図
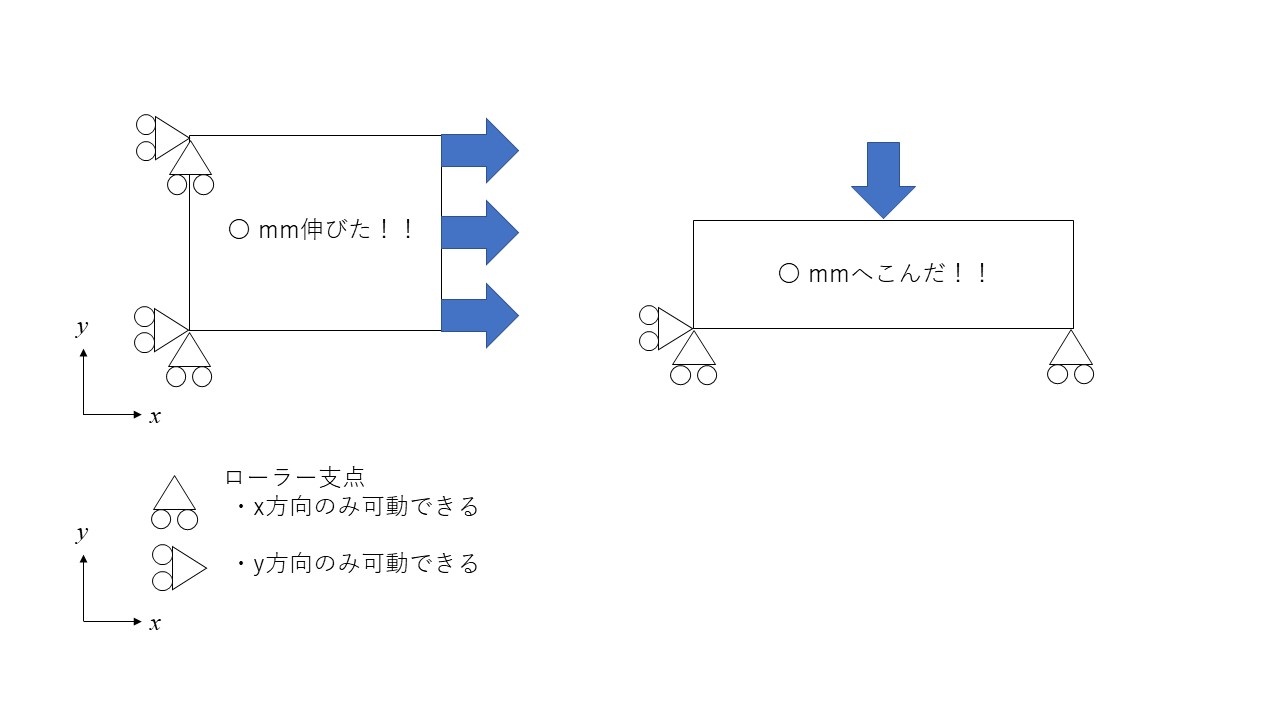
Fig.
作業環境
言語:Python 3.7.3
numpy==1.15.4+mkl
matplotlib==3.1.3
プログラムの説明
全体の流れは以下のようになります。
- 変数の定義
- メッシュ分割した要素をClassを用いて記述
- 要素(インスタンス)の作成
- 全体変位の導出
それではプログラムの説明に入ろうと思います。
1. モジュールのインポート
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib.patches as patches
2. 変数の定義
2.1 変数の定義(いじる部分)
この節に記述しているプログラムの変数を変更することにより、様々な条件で弾性有限要素法解析を行うことができます。まず解析モデルおよび解析条件を説明していきます。
- 解析モデルの寸法
解析モデルは縦1 \mathrm{\;m} 2 \mathrm{\;m} 1 \mathrm{\;m} rect) - 拘束条件
図3 - 荷重条件
図3 10\times10^6 \mathrm{N}

Fig.3
続いて要素の分割方法や材料の物性値の説明をしていきます。
- メッシュ分割
今回の直方体は縦1 \mathrm{\;m} 2 \mathrm{\;m} 0.1 \mathrm{\;m} 0.1 \mathrm{\;m} size)。したがって、y 10 x 20 200 4 - 要素番号の割り振り
図3 - 材料物性値
今回は合金鋼(ヤング率:2.1\times10^ {11} \mathrm{N/m^{2}} 0.28

Fig.4
# 解析対象の形状
rect = [2, 1, 1] # #直方体のx,y方向の長さおよび奥行 rect = [x,y,t] Unit m
size = [0.1, 0.1] # メッシュサイズ[x,y] Unit m
D_num = 1 # 厚板(平面ひずみ)0 薄板(平面応力)1
# 荷重条件
# x方向の荷重
f_x = np.array([[rect[0], 0, 10*10**6], [rect[0], rect[1], 10*10**6]]
) # [x,y,f_x] Unit [m,m,N]
# y方向の荷重(例)
# f_y = np.array([[rect[0], 0, 10*10**6], [rect[0], rect[1], 10*10**6]]
# ) # [x,y,f_y] Unit [m,m,N]
# 荷重をかけたくない場合
# f_x = np.array([[0, 0, 0]])
f_y = np.array([[0, 0, 0]])
# 拘束条件(辺で拘束)
u_xx = [0] # x座標が0 mのx方向に対する変位を拘束
u_xy = [0] # x座標が0 mのy方向に対する変位を拘束
# 材料物性値
E = 2.1*10 ** 11 # 合金鋼のヤング率
nu = 0.28 # ポアソン比
enhance = 410 # 結果をそのまま描画すると変形の様子が分かりづらいので誇張して描画する。
2.2 変数の定義(いじらない部分)
# 四角形要素(三角形要素に比べて要素内のひづみが分布しているので制度が良い)
Nx = int(rect[0]/size[0]) # 要素番号(x方向)
Ny = int(rect[1]/size[1]) # 要素番号(y方向)
detA = float(size[0]*size[1])
xi_eta = np.array([[-1/np.sqrt(3), -1/np.sqrt(3)], [1/np.sqrt(3), -1/np.sqrt(3)],
[1/np.sqrt(3), 1/np.sqrt(3)], [-1/np.sqrt(3), 1/np.sqrt(3)]]) # ξ-η座標系の各要素内で取得する4つの座標
elements = [0]*Nx*Ny # 要素番号の総数(instanceの初期化)
all_node = np.arange((Nx+1)*(Ny+1)).reshape(Ny+1, Nx+1) # image
# ↑を参照しやすいように↓で要素を横一列にする
all_node = np.vstack((np.arange((Nx+1)*Ny), (Nx+1+np.arange((Nx+1)*Ny))))
x_coordinate = np.tile(np.arange(Nx+1, dtype='float64')*size[0],
Ny+1).reshape(Ny+1, Nx+1).reshape(-1)
y_coordinate = np.array([[x * size[1]]*(Nx+1)
for x in range(Ny, -1, -1)], dtype='float64').reshape(Ny+1, Nx+1).reshape(-1)
K = np.zeros(((Nx+1)*(Ny+1)*2, (Nx+1)*(Ny+1)*2))
3. メッシュ分割した要素をClassを用いて記述
弾性有限要素法は次に示す方程式を解くことが目的です。
この方程式は全体剛性方程式と呼ばれており、全体剛性マトリックス
節点力は解析対象に加わる力で、初期条件で定めています。全体剛性マトリックスは、解析対象がどのように変形するかを表した行列であり、ヤング率やポアソン比などの情報から求めることができます。
今回の問題では、既知数である全体剛性マトリックス
全体剛性マトリックス
以下のプログラムは ElementClass を定義しています。 ElementClass は各要素の剛性マトリックス
class Element:
def __init__(self, element, element_xy=np.array([[-1, -1], [1, -1], [1, 1], [-1, 1]])):
self.element = element
self.node = np.zeros((4)) # 各elementに対応するnode
self.K_assort = np.zeros((2, 8))
self.D = np.vstack((E/((1+nu)*(1-2*nu))*np.array([[[1-nu, nu, 0], [nu, 1-nu, 0], [0, 0, (1-2*nu)/2]]]),
E/(1-nu ** 2)*np.array([[[1, nu, 0], [nu, 1, 0], [0, 0, (1-nu)/2]]])))
self.Km = np.zeros((8, 8)) # m番目の要素番号の剛性マトリックス
self.KmG = np.zeros(((Nx+1)*(Ny+1)*2, (Nx+1)*(Ny+1)*2)) # Kmを全体剛性マトリックスの行列サイズに拡張するための変数
self.element_xy = element_xy
self.J = np.zeros((4))
self.delN = np.zeros((4, 8))
self.Bm = np.zeros((4, 3, 8))
for i in range(4):
self.J[i] = (1/8)*((self.element_xy[0, 0]-self.element_xy[2, 0])*(self.element_xy[1, 1]-self.element_xy[3, 1])
- (self.element_xy[1, 0]-self.element_xy[3, 0]) *
(self.element_xy[0, 1]-self.element_xy[2, 1])
+ xi_eta[i, 0]*(self.element_xy[2, 0]-self.element_xy[3, 0]) *
(self.element_xy[0, 1]-self.element_xy[1, 1])
- (self.element_xy[0, 0]-self.element_xy[1, 0]) *
(self.element_xy[2, 1]-self.element_xy[3, 1])
+ xi_eta[i, 1]*(self.element_xy[1, 0]-self.element_xy[2, 0]) *
(self.element_xy[0, 1]-self.element_xy[3, 1])
- (self.element_xy[0, 0]-self.element_xy[3, 0])*(self.element_xy[1, 1]-self.element_xy[2, 1]))
self.delN[i] = (1/(8*abs(self.J[i])))*np.array([
self.element_xy[1, 1]-self.element_xy[3, 1]+xi_eta[i, 0]*( # 1
self.element_xy[3, 1]-self.element_xy[2, 1])+xi_eta[i, 1]*(self.element_xy[2, 1]-self.element_xy[1, 1]),
self.element_xy[3, 0]-self.element_xy[1, 0]+xi_eta[i, 0]*( # 2
self.element_xy[2, 0]-self.element_xy[3, 0])+xi_eta[i, 1]*(self.element_xy[1, 0]-self.element_xy[2, 0]),
self.element_xy[2, 1]-self.element_xy[0, 1]+xi_eta[i, 0]*( # 3
self.element_xy[2, 1]-self.element_xy[3, 1])+xi_eta[i, 1]*(self.element_xy[0, 1]-self.element_xy[3, 1]),
self.element_xy[0, 0]-self.element_xy[2, 0]+xi_eta[i, 0]*( # 4
self.element_xy[3, 0]-self.element_xy[2, 0])+xi_eta[i, 1]*(self.element_xy[0, 0]-self.element_xy[3, 0]),
self.element_xy[3, 1]-self.element_xy[1, 1]+xi_eta[i, 0]*( # 5
self.element_xy[0, 1]-self.element_xy[1, 1])+xi_eta[i, 1]*(self.element_xy[3, 1]-self.element_xy[0, 1]),
self.element_xy[1, 0]-self.element_xy[3, 0]+xi_eta[i, 0]*( # 6
self.element_xy[1, 0]-self.element_xy[0, 0])+xi_eta[i, 1]*(self.element_xy[0, 0]-self.element_xy[3, 0]),
self.element_xy[0, 1]-self.element_xy[2, 1]+xi_eta[i, 0]*( # 7
self.element_xy[1, 1]-self.element_xy[0, 1])+xi_eta[i, 1]*(self.element_xy[1, 1]-self.element_xy[2, 1]),
self.element_xy[2, 0]-self.element_xy[0, 0]+xi_eta[i, 0]*( # 8
self.element_xy[0, 0]-self.element_xy[1, 0])+xi_eta[i, 1]*(self.element_xy[2, 0]-self.element_xy[1, 0])])
self.Bm[i] = np.array([[self.delN[i, 0], 0, self.delN[i, 2], 0, self.delN[i, 4], 0, self.delN[i, 6], 0],
[0, self.delN[i, 1], 0, self.delN[i, 3], 0,
self.delN[i, 5], 0, self.delN[i, 7]],
[self.delN[i, 1], self.delN[i, 0], self.delN[i, 3], self.delN[i, 2], self.delN[i, 5], self.delN[i, 4], self.delN[i, 7], self.delN[i, 6]]])
def pro_makeK(self): # proceed
self.makeKm() # 要素番号m番目の剛性マトリックスの作成
self.K_assort_node() # elementの節点番号の対応付け([1,1,3,3,2,2,4,4]みたいなoutput)
self.makeKmG() # 作成した剛性マトリックスの行列サイズを全体剛性マトリックスに合うように拡張する。
def makeKm(self):
self.Km = 0
for i in range(4):
self.Km = self.Km + rect[2]*self.J[i] * \
self.Bm[i].T @ self.D[D_num] @ self.Bm[i]
def K_assort_node(self):
self.K_assort[1] = np.tile(np.array([1, 2]), 4) # x,y,x,y,x,y
self.node[0] = all_node[1, self.element+self.element//Nx] # 左下
self.node[1] = all_node[1, self.element+1+self.element//Nx] # 右下
self.node[2] = all_node[0, self.element+1+self.element//Nx] # 右上
self.node[3] = all_node[0, self.element+self.element//Nx] # 左上
for i in range(4):
self.K_assort[0, i*2] = int(self.node[i])
self.K_assort[0, i*2+1] = int(self.node[i])
def makeKmG(self):
for i in range(8):
for j in range(8):
self.KmG[int(2*(self.K_assort[0, i]) +
self.K_assort[1, i]-1),
int(2*(self.K_assort[0, j]) +
self.K_assort[1, j]-1)]\
= self.Km[i, j]
4. インスタンスの作成
全要素に ElementClassのインスタンスを代入します。
次に、全体剛性マトリックス
for i in range(Nx*Ny):
elements[i] = Element(i)
elements[i].pro_makeK()
K = K + elements[i].KmG
5. 節点力を作成
改めて全体剛性方程式は次の式で表されます。
以下のプログラムでは全体剛性方程式の右辺である節点力
def makeU(K):
# 全体剛性方程式右辺(節点力)を作成していく
# 各要素の変位と力について既知であるか未知であるか振り分けていく
syoki = np.array([[True] for i in range((Nx+1)*(Ny+1)*2)]
).reshape((Ny+1), (Nx+1), 2) # False=変位が既知、True=力が既知
for i in u_xx:
syoki[:, i, 0] = [False] # syoki[行(y),列(x),x方向拘束]
for i in u_xy:
syoki[:, i, 1] = [False] # syoki[行(y),列(x),y方向拘束]
# 既知力・既知変位・全体剛性マトリックスの初期化
f = np.zeros((Nx+1)*(Ny+1)*2).reshape((Ny+1), (Nx+1), 2) # 既知力f
u = np.zeros((Nx+1)*(Ny+1)*2).reshape((Ny+1), (Nx+1), 2) # 既知変位u
F = np.zeros((Nx+1)*(Ny+1)*2) # 全体剛性マトリックス右辺
# 今まで力を加える箇所を長さで指定していたが節点番号で指定しなおす
f_x[:, 0] = f_x[:, 0]*int(1/size[0]) # メッシュの分割数にx座標を合わせる
f_x[:, 1] = f_x[:, 1]*int(1/size[0])
f_y[:, 0] = f_y[:, 0]*int(1/size[1]) # メッシュの分割数にx座標を合わせる
f_y[:, 1] = f_y[:, 1]*int(1/size[1])
for i in range(f_x.shape[0]):
f[f_x[i, 1], f_x[i, 0], 0] = f_x[i, 2] # f[y座標(行),x座標(列),0...x方向の荷重]
for i in range(f_y.shape[0]):
f[f_y[i, 1], f_y[i, 0], 1] = f_y[i, 2] # f[y座標(行),x座標(列),1...y方向の荷重]
syoki = syoki.reshape(-1)
f = f.reshape(-1)
u = u.reshape(-1)
for i in range((Nx+1)*(Ny+1)*2):
for j in range((Nx+1)*(Ny+1)*2):
if syoki[j] == [False]:
F[i] = f[i] - u[j]*K[i, j]
# (U)を導出するために[K]を計算コストが低い形にする
# ある要素の変位が既知の場合、その要素に関わるKは簡単な形にできる
for i in range((Nx+1)*(Ny+1)*2):
if syoki[i] == [False]:
K[i, :] = 0
K[:, i] = 0
K[i, i] = 1
# 初期条件により変位がすでに分かっている行列要素は削除する。
plus = 0
for i in range((Nx+1)*(Ny+1)*2):
if syoki[i] == [False]:
K = np.delete(K, i-plus, axis=0)
K = np.delete(K, i-plus, axis=1)
F = np.delete(F, i-plus, axis=0)
plus += 1
# makeU
K = np.matrix(K)
F = np.matrix(F).T
U = np.linalg.pinv(K)*F
# Uを既知も含めて表示する。
U_all = np.zeros(((Nx+1)*(Ny+1)*2, 1))
count = 0
for i in range(len(syoki)):
if syoki[i] == [True]:
U_all[i] = U[count]
count = count+1
U_all = U_all.reshape((Ny+1)*(Nx+1), 2)
# print(U_all) # 結論(全ての要素の変位)
print(U_all[-1]*10 ** 3) # 最後の要素番号(解析対象の右端)の変位を取得している。
return U_all
6. 画面表示
この節は、変形の結果を描画するためのプログラムを記述しています。
def plot_line(x_coordinate, y_coordinate, Colar='black'):
# purpose...モデルのラインを引く
# input...x,y座標
# output...変位前の解析モデルの外形
# 辺を抽出しやすいように変形
x_coordinate = x_coordinate.reshape(Ny+1, Nx+1)
y_coordinate = y_coordinate.reshape(Ny+1, Nx+1)
# 両軸のアスペクト比を合わせる
for i in range(Ny+1): # 横線
plt.plot(x_coordinate[i], y_coordinate[i],
marker='.', color=Colar)
for i in range(Nx+1): # 縦線
plt.plot(x_coordinate[:, i], y_coordinate[:, i],
marker='.', color=Colar)
def plot_result(U_all):
# purpose...変位後の解析モデルを描画する
# input...全座標での変位
# output...変位後の解析モデルの外形
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_aspect('equal')
np.set_printoptions(precision=3)
plot_line(x_coordinate, y_coordinate, 'black')
for i in range((Nx+1)*(Ny+1)):
plt.plot(x_coordinate[i], y_coordinate[i], marker='.', color='black')
for i in range((Nx+1)*(Ny+1)):
x_coordinate[i] = x_coordinate[i] + U_all[i, 0] * enhance # 誇張して表現してる
y_coordinate[i] = y_coordinate[i] + U_all[i, 1] * enhance
plot_line(x_coordinate, y_coordinate, 'red')
for i in range((Nx+1)*(Ny+1)):
x_coordinate[i] = x_coordinate[i] \
- U_all[i, 0] * enhance + U_all[i, 0] # 誇張から元に直す
y_coordinate[i] = y_coordinate[i] \
- U_all[i, 1] * enhance + U_all[i, 1]
for i in range((Nx+1)*(Ny+1)):
# plt.text(x_coordinate[i] - U_all[i, 0] + U_all[i, 0] * enhance, y_coordinate[i] - U_all[i, 0] + U_all[i, 1] * enhance, '({x}, {y})'.fomathrmat(
# x = x_coordinate[i], y = y_coordinate[i]), fontsize=10, color='red')
plt.plot(x_coordinate[i] + U_all[i, 0] * enhance,
y_coordinate[i] + U_all[i, 1] * enhance, marker='.', color='red')
plt.axis('scaled')
ax.set_aspect('equal')
plt.show()
# plt.savefig('data/dst/matplotlib_patches.png')
7. 結果の表示
U_all = makeU(K) # 全体変位Uを導出
plot_result(U_all) # 結果表示
8. プログラムの実行
StaticAnalysis.pyという名前でファイルを作成し実行します。(図
python ./StaticAnalysis.py
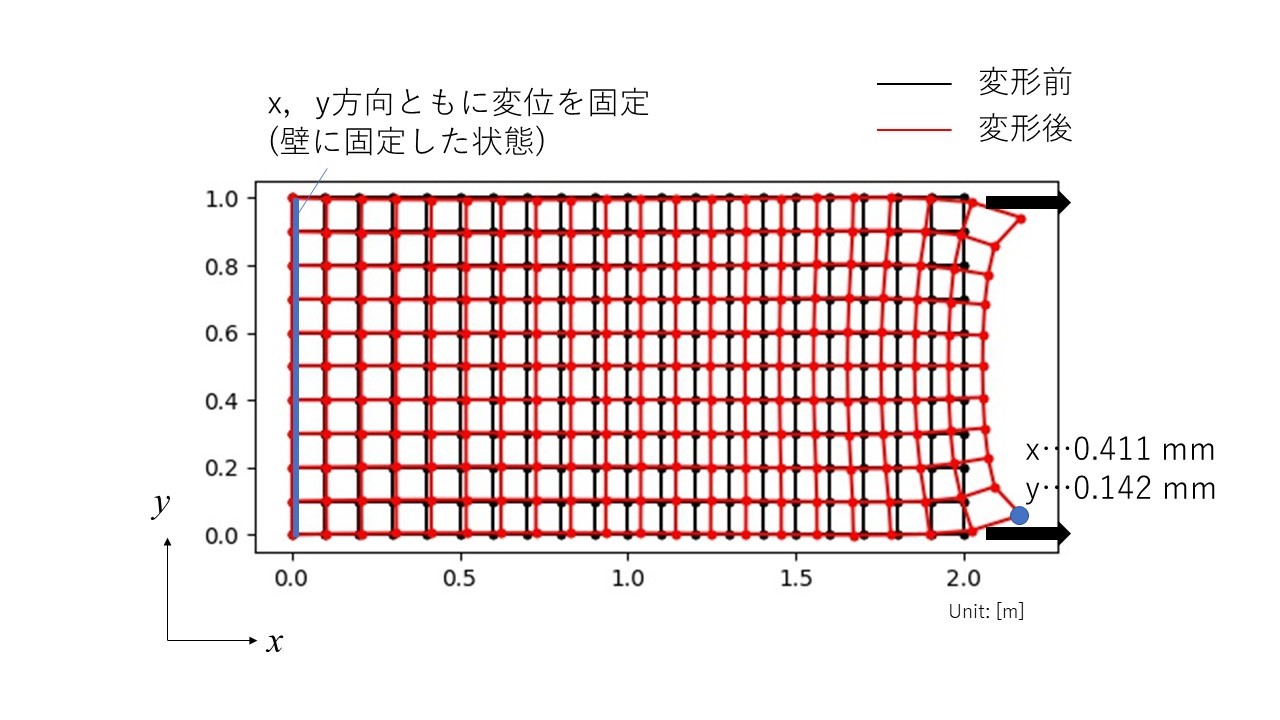
Fig.
みなさんが想像した変形の結果と一致しましたか?
変形量はあまりにも微小なので結果をそのまま描画すると変形の様子が分かりづらいです。したがって一般的な有限要素法ソフトでは結果を誇張して描画することが多いです。今回はスケールを
解析対象に力を加えた箇所(図
SolidWorksで比較してみる
本プログラムの解析結果と市販CADソフトSolidWorksでの解析結果を比較してみます。
-
x

Fig.6 x
力を加えている2 x 0.4874 \mathrm{\;mm} 0.41057 \mathrm{\;mm} -
y

Fig.7 y
力を加えている2 y 0.2182 \mathrm{\;mm} 0.14231 \mathrm{\;mm}
考察
本プログラムとSolidWorksでなぜ解析結果に差が生じているのか考察を行っていきます。
本プログラムの要素数は
よって本プログラムの解析モデルを更に多い要素数に分割します。
プログラム変更内容は以下のとおりです。
- size = [0.1, 0.1]
+ size = [0.05, 0.05]
・結果

Fig.
SolidWorks...
SolidWorks...
SolidWorksと
参考文献
[1] 吉野雅彦、天谷賢治、Excel による有限要素法 -弾性・弾塑性・ポアソン方
程式-、朝倉書店、(2006)、pp.60-66
Discussion