💉

Stan ユーザーのための層別解析入門の準備

に公開
R
Stan
因果推論
tech

はじめに

因果推論の手法として知られる層別解析を勉強する過程で，私自身がつまずいた前提みたいな部分について書いていく．前提みたいな部分というのは，そもそもこれなんの計算してるの？　というようなことで，層別解析のやり方についての解説まで至らない．なのでタイトルは「層別解析入門」ではなく「層別解析入門の準備」とした．

結論を先取りすると，おおむね下の箇条書きのようなことを述べる．

  • 介入後の結果変数は観察データのモデルの結果変数とは（パラメータを共有する）別の確率変数だと思うのがいい
  • 観察データのモデルが決まっても，それだけでは介入後を表すモデルは一意に決まらない
  • 因果グラフも加えて仮定するとそれが一意に決まる

確率的グラフィカルモデルを用いた解説のスタイルは主に下記の文献を参考にした．

使用したコードの全体は記事の末尾にまとめてある．

確率的グラフィカルモデルを作る

まず（疑似）乱数を使ったシミュレーションをやってみたい．次の表で表せるような同時分布からの乱数をR言語（または適当な統計ソフト）を使って得るにはどうすればいいだろうか．

y x z 確率
0 0 0 0.200
1 0 0 0.050
0 1 0 0.200
1 1 0 0.200
0 0 1 0.050
1 0 1 0.245
0 1 1 0.005
1 1 1 0.050

3つ組の確率変数 y, x, z はそれぞれ単位時間経過時点での症状の回復（0が未回復で1が回復），薬の投与（0が薬なしで1が薬あり），重症度（0が軽症で1が重症）を表すことにする．

このモンテカルロ・シミュレーションでは（単変量の）2項分布に従う乱数を生成する rbinom 関数を使うことにしよう．

条件付き確率の定義から，同時分布は次のようにも書ける．

\begin{aligned} p(x,y,z) = p(y|x,z)p(x,z) \\ = p(y|x,z)p(x|z)p(z).\tag{1} \end{aligned}

右辺は単変量の2項分布の積で表せた．2項分布のパラメータを下記のリストのようにおく．

  • p(y=1|z,x) = \xi_{z,x}
  • p(x=1|z) = \psi_x
  • p(z=1) = \gamma

これは (Y, X, Z) が単変量の rbinom 関数でサンプリングできることを意味する．R のコードはたとえば次のようになる．

rand_case1 = function(n, xi, psi, gamma){
  ## draw x given by z
  z = rbinom(n, 1, gamma)
  x = rbinom(n, 1, psi[z+1]) #R の配列のインデックスは 1 からはじまるため，1 足して z=0 のときを 1行目, z=1 のときを 2 行目にしている
  y = rbinom(n, 1, xi[cbind(z+1,x+1)])
  return(data.frame(Y=y, X=x, Z=z))
}

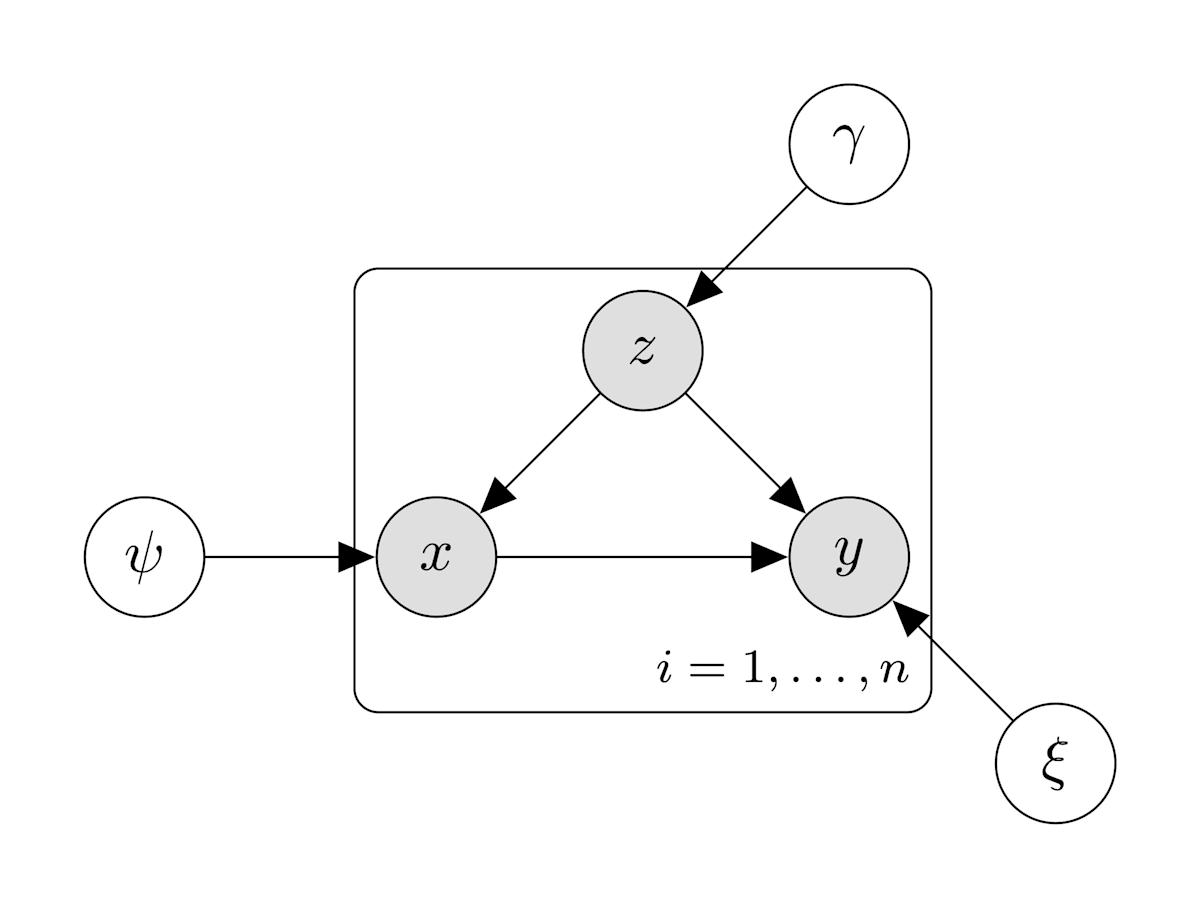
p(x|z) のような従属関係を z \rightarrow x と表すことにすると，同時分布は下の図のようなグラフィカルモデルでも表せる．


(1)の方針の確率的グラフィカルモデル

このように向きがあり，元のノードに戻るパスがないグラフを有向非巡回グラフ（Directed Acyclic Graph; DAG）と呼ぶ．

さて，(1)のような分解は一通りに限らない．たとえば次のようにしてもいい．

\begin{aligned} p(x,y,z) &= p(y|x,z)P(x,z) \\ &= p(y|x,z)p(z|x)p(x)).\tag{2} \end{aligned}

ここではパラメータを下記のリストのようにおく．

  • p(y=1|z,x) = \xi_{z,x}
  • p(z=1|x) = \phi_x
  • p(x=1) = \delta

これに対応する R のコードはたとえば次のように書ける．

rand_case2 = function(n, xi, phi, delta){
  ## draw z given by x
  x = rbinom(n, 1, delta)
  z = rbinom(n, 1, phi[x+1])
  y = rbinom(n, 1, xi[cbind(z+1,x+1)])  
  return(data.frame(Y=y,X=x,Z=z))
}

グラフィカルモデルは下の図のようになる．


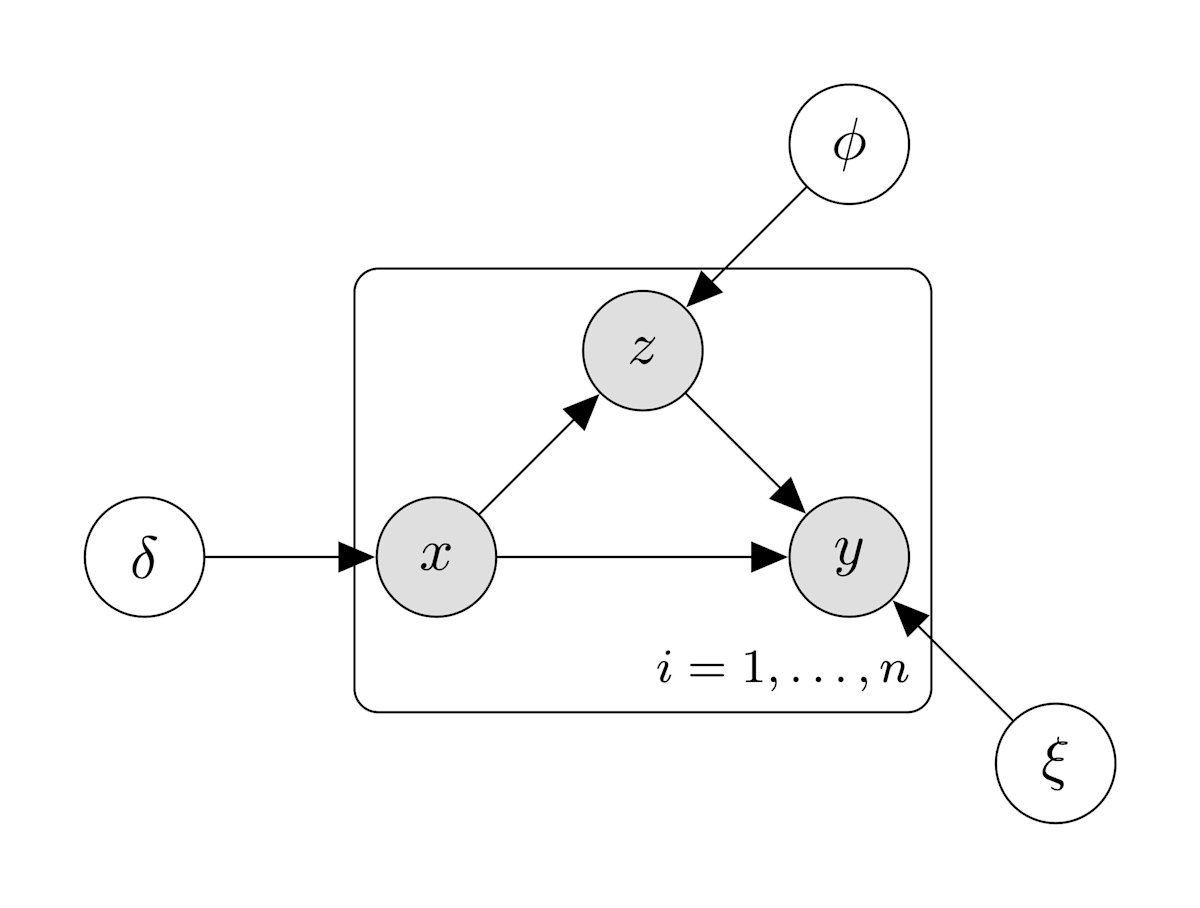
(２)の方針の確率的グラフィカルモデル

観測されない潜在変数（latent variable）は白丸，観測される変数をグレーの丸で表している．

試しに乱数を10000個サンプルして平均を取る．

PY_x = group_by(df_prob, x) %>% 
  summarise(p = sum(y*p)/sum(p))

PY_xz = group_by(df_prob, x, z) %>% 
  summarise(p = sum(y*p)/sum(p))

PX_z = group_by(df_prob,  z) %>% 
  summarise(p = sum(x*p)/sum(p))

PZ_x = group_by(df_prob,  x) %>% 
  summarise(p = sum(z*p)/sum(p))

PX = summarise(df_prob, p = sum(x*p)/sum(p))
PZ = summarise(df_prob, p = sum(z*p)/sum(p))

Xi = matrix(PY_xz$p, 2, 2)
rownames(Xi) = paste0("z", 0:1)
colnames(Xi) = paste0("x", 0:1)

dat1 = rand_case1(n = 10000, xi = Xi, psi = PX_z$p, gamma = PZ$p)
tab1 = group_by(dat1,Y,X,Z) %>% 
  tally() %>% 
  ungroup() %>% 
  mutate(p=n/sum(n)) %>% 
  arrange(Z,X,Y)


dat2 = rand_case2(n = 10000, xi = Xi, phi = PZ_x$p, delta = PX$p)
tab2 = group_by(dat2,Y,X,Z) %>% 
  tally() %>% 
  ungroup() %>% 
  mutate(p=n/sum(n)) %>% 
  arrange(Z,X,Y)

kable(cbind(df_prob, "rand_case1" = tab1$p, "rand_case2"=tab2$p),
      digits=3)

結果は下の表のようになった．

y x z p rand_case1 rand_case2
0 0 0 0.200 0.206 0.205
1 0 0 0.050 0.049 0.046
0 1 0 0.200 0.200 0.198
1 1 0 0.200 0.195 0.195
0 0 1 0.050 0.048 0.052
1 0 1 0.245 0.249 0.247
0 1 1 0.005 0.005 0.004
1 1 1 0.050 0.049 0.052

"p" の列がこのシミュレーションで最初に設定した真値である．rand_case1 と rand_case2，どちらの書き方でも同じ分布が得られていそうなことがわかる．

そして，このような形でモデルが書けたら，事後分布に従う乱数をサンプルするための Stan のコードも書くことができる．

パラメータもふくめて(1)の方針の確率的グラフィカルモデルが表す同時分布をもう少しちゃんと書くと次のようになる．

\begin{aligned} p&(x,y,z,\xi, \psi, \gamma) \\ &= p(\xi)p(\psi)p(\gamma) \left(\prod_{i=1}^n p(y_i|x_i,z_i,\xi)p(x|z, \psi)p(z|\gamma)\right). \tag{1'} \end{aligned}

パラメータ（潜在変数）の事後分布は p(\xi, \psi, \gamma | x,y,z) であるから，データ x, y, z を所与として，同時分布が定まれば事後分布も定まる．

(1) の場合：

//case1.stan
data{
  int N;
  array[N] int<lower=0,upper=1> Y;
  array[N] int<lower=0,upper=1> Z;
  array[N] int<lower=0,upper=1> X;
  real<lower=0> alpha;
}
parameters{
    matrix<lower=0, upper=1>[2,2] Xi;
    vector<lower=0, upper=1>[2] psi;
    real<lower=0, upper=1> gamma;
}
model{
  for(i in 1:N){
    Z[i] ~ bernoulli(gamma);
    X[i] ~ bernoulli(psi[Z[i]+1]);
    Y[i] ~ bernoulli(Xi[Z[i]+1, X[i]+1]);
  }
  to_vector(Xi) ~ beta(alpha, alpha);
  gamma ~ beta(alpha, alpha);
  psi ~ beta(alpha, alpha);
}

この Stan のコードの ~ の現れる行はすべて，(1') の右辺の対数を lp__ という変数に足し込む操作を意味する．

alpha は事前分布のパラメータとして導入したが今回はあまり活躍せず，ずっと 1 （一様分布）にしている．

(2) の場合：

#case2.stan
data{
  int N;
  array[N] int<lower=0,upper=1> Y;
  array[N] int<lower=0,upper=1> Z;
  array[N] int<lower=0,upper=1> X;
  real<lower=0> alpha;
}
parameters{
    matrix<lower=0, upper=1>[2,2] Xi;
    vector<lower=0, upper=1>[2] phi;
    real<lower=0, upper=1> delta;
}
model{
  for(i in 1:N){
    Z[i] ~ bernoulli(phi[X[i]+1]);
    X[i] ~ bernoulli(delta);
    Y[i] ~ bernoulli(Xi[Z[i]+1, X[i]+1]);
  }
  to_vector(Xi) ~ beta(alpha, alpha);
  delta ~ beta(alpha, alpha);
  phi ~ beta(alpha, alpha);
}

(1) と (2) は同じ同時分布を表している．変数変換によって \psi と \gamma から \phi と \delta をつくることもできる．

条件付き確率の定義から p(x) は次のようにも表せる．

\begin{aligned} p(x) &= \sum_z p(x,z) \\ &= \sum_z p(x|z)p(z) \end{aligned}

この関係から \delta は次式のように表せる．

\begin{aligned} \delta &= p(x=1) \\ &= \psi_0 \cdot (1-\gamma)+\psi_1 \cdot\gamma. \end{aligned}

また， p(z|x) は次のように表せる．

\begin{aligned} p(z|x) &= \frac{p(x,z)}{p(z)}\\ & =\frac{p(x|z)p(x)}{p(z)} \end{aligned}

この関係を用いて \phi は

\begin{aligned} \phi_0 &= p(z=1|x=0) \\ &= \frac{(1-\psi_1)\gamma}{1-\delta} \end{aligned}

および，

\begin{aligned} \phi_1 &= p(z=1|x=1) \\ &= \frac{\psi_1 \gamma}{\delta} \end{aligned}

である． \phi と \delta についても事後分布に従がうサンプルを得るには　generated quantities ブロックを次のように書けばよい．

#case1.stan
generated quantities{
  real<lower=0, upper=1> delta;
  vector<lower=0, upper=1>[2] phi;
  delta = psi[1]*(1-gamma) + psi[2]*gamma;
  phi[1] = (1-psi[2])*gamma/(1-delta);
  phi[2] = psi[2]*gamma/delta;
}

同様に \phi と \delta から \psi と \gamma をつくることもできる．

p(z) は次のように表せる．

p(z) = \sum_x p(z|x)p(x)

これより \gamma は，

\begin{aligned} \gamma &= p(z=1) \\ &= \phi_0 \cdot (1-\delta)+\phi_1 \cdot\delta. \end{aligned}

また p(x|z) は次のように表せる．

p(x|z) = \frac{p(z|x)p(x)}{p(z)}

この関係を用いて \psi は

\begin{aligned} \psi_0 &= p(x=1|z=0) \\ &= \frac{(1-\phi_0)\delta}{\gamma} \end{aligned}

および，

\begin{aligned} \psi_1 &= p(x=1|z=1) \\ &= \frac{(1-\phi_1)\delta}{\gamma} \end{aligned}

である．

#case2.stan
generated quantities{
  real<lower=0, upper=1> gamma;
  vector<lower=0, upper=1>[2] psi;
  gamma = phi[1]*(1-delta) + phi[2]*delta;
  psi[1] = (1-phi[2])*delta/(1-gamma);
  psi[2] = phi[2]*delta/gamma;
}

サンプルサイズを n=500 としたシミュレーションデータに対して上の Stan のコードを実行してみる．

次の図からMCMCの系列が定常分布に収束した様子がうかがえる．


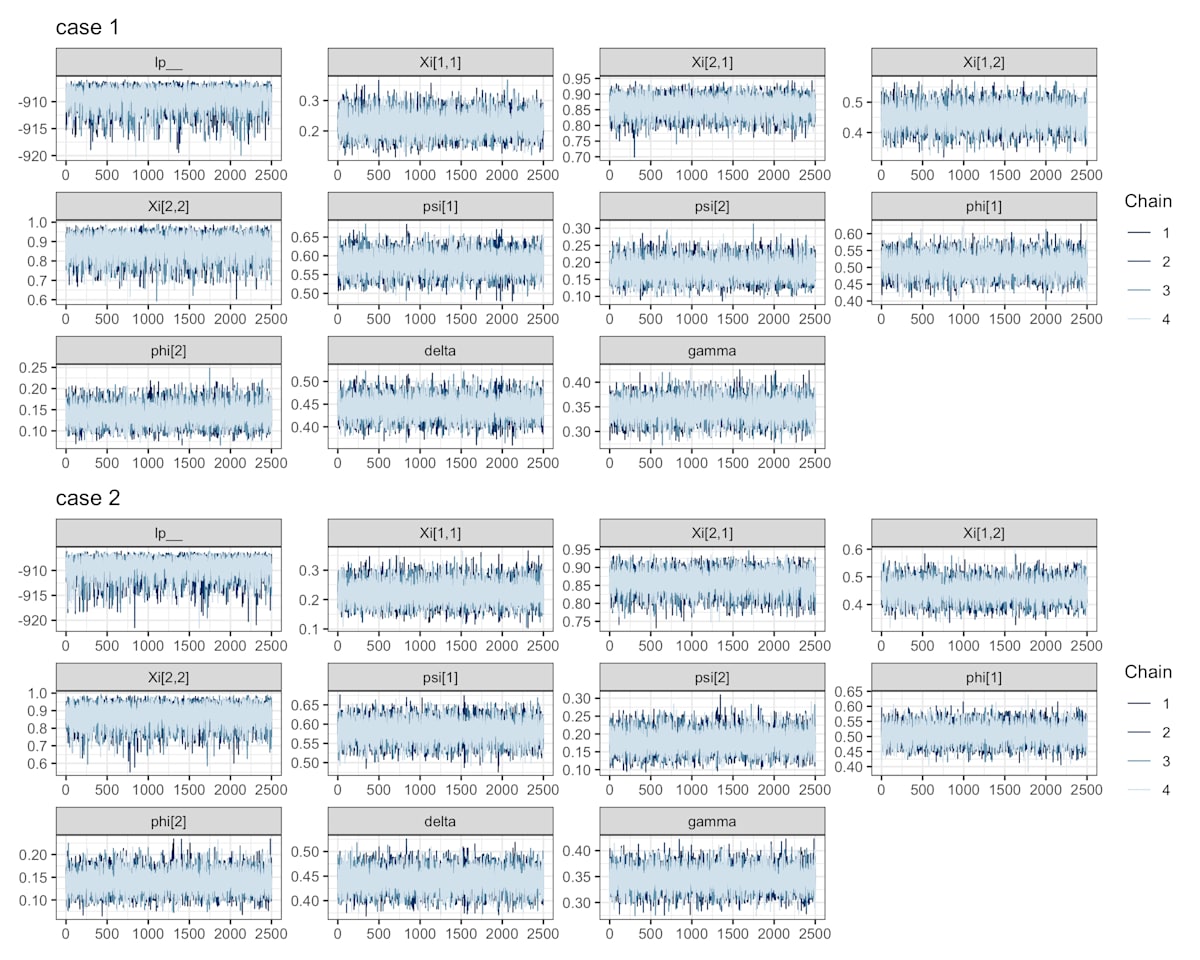
トレースプロット

各パラメータの事後分布の経験分布関数をプロットする．


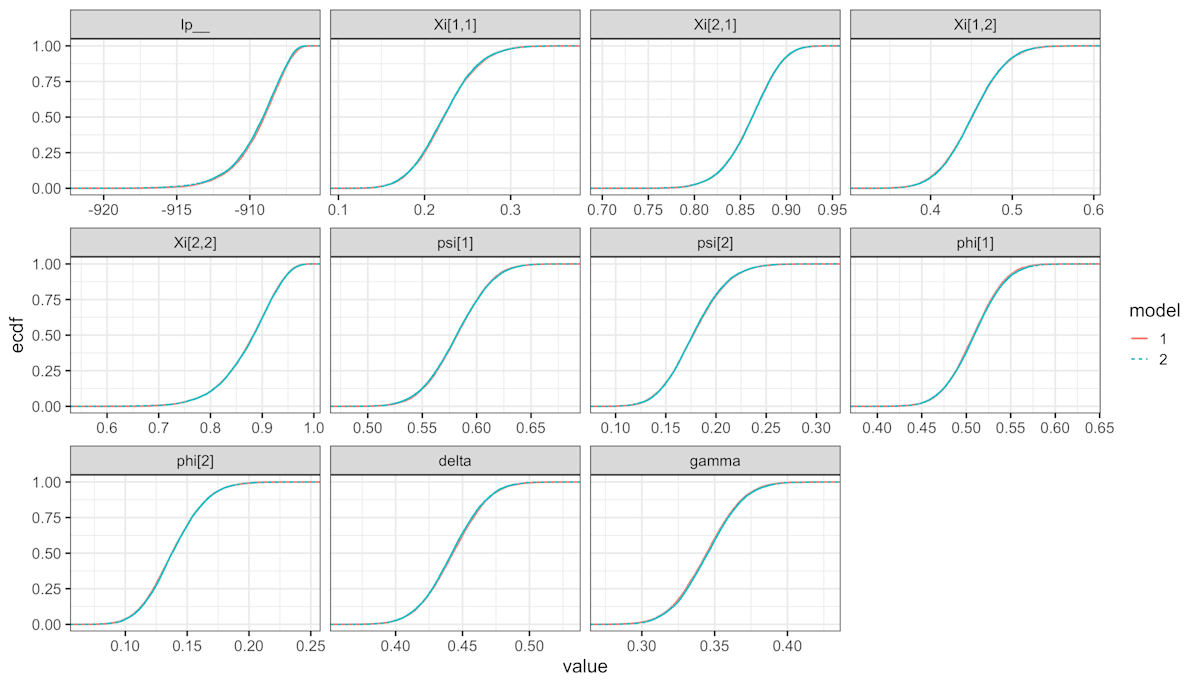
パラメータの事後分布

case1.stan と case2.stan を それぞれ model 1, 2 として色分けしたが重なっていてほとんど違いが見えない．つまり，ほぼ同じ事後分布が得られているとわかる．繰り返しになるが lp__ は同時確率の対数の総和である．

各パラメータの平均と標準誤差（この場合は事後分布の標準偏差のこと）は下の表の通り．

variable model1.mean model1.sd model2.mean model2.sd true
Xi[1,1] 0.22 0.04 0.22 0.04 0.20
Xi[2,1] 0.86 0.03 0.86 0.03 0.83
Xi[1,2] 0.45 0.04 0.45 0.04 0.50
Xi[2,2] 0.88 0.06 0.88 0.06 0.91
psi[1] 0.58 0.03 0.58 0.03 0.62
psi[2] 0.18 0.03 0.18 0.03 0.16
phi[1] 0.51 0.03 0.51 0.03 0.54
phi[2] 0.14 0.02 0.14 0.02 0.12
delta 0.44 0.02 0.44 0.02 0.35
gamma 0.34 0.02 0.35 0.02 0.46

因果的グラフィカルモデルを作る

ここまでで同時分布は推定できた．仮にこのような分析を行い「この変数 x が 1 のとき結果 y も 1 がでやすくなります」と報告したとしよう．そうしたら次のステップで「じゃあ x=1 にしてみよう！」となるのは自然な発想だと思う．

一方でこれまでの考察で同時分布が定まっても x=1 に固定したときの分布は一意でないことがわかる．

つまり (1) の方針でサンプリングする場合， (2) の方針でサンプリングする場合で x=1 に固定したときの y の分布は異なる．

(1) の方針でのサンプリングを x=1 に固定した場合を Stan のコードで書くと次のようになる．

#case1
generated quantities{
    int Zast = bernoulli_rng(gamma)+1;
    int Yast0 = bernoulli_rng(Xi[Zast,1]);
    int Yast1 = bernoulli_rng(Xi[Zast,2]);
}

この Stan のコードは下の図のようなグラフィカルモデルを考えることに相当する．


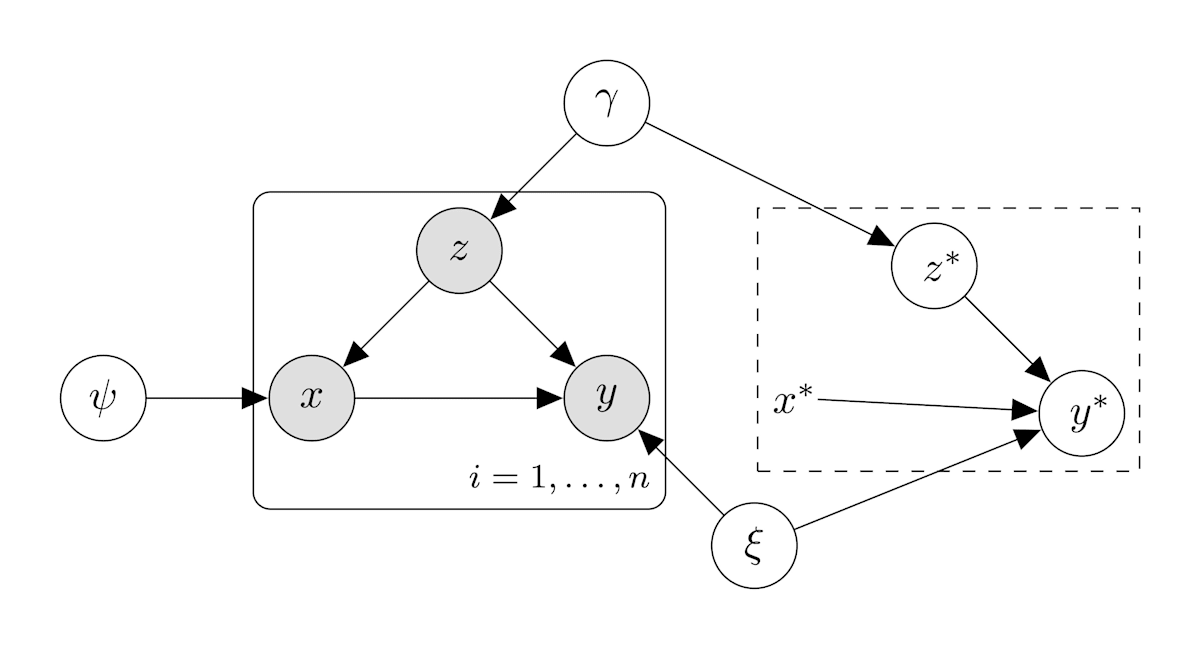
(1)の方針の確率的グラフィカルモデル2

x に入るすべてのパスに関わらず x=a に固定する操作を 介入（intervention）と呼び，do(x=a) などと書く．do(x=a) のとき， y に対応する確率変数 y^\ast = y(do(x=a)) を 潜在結果変数（potential outcome）と呼ぶ．図の点線の中は介入後の潜在結果変数のモデルを表している．

(2) の方針でサンプリングする場合は，次のようになる．

#case2
generated quantities{
  int Yast0;
  int Yast1;
  int Zast0;
  int Zast1;
  Zast0 = bernoulli_rng(phi[1])+1;
  Zast1 = bernoulli_rng(phi[2])+1;
  Yast0 = bernoulli_rng(Xi[Zast0,1]);
  Yast1 = bernoulli_rng(Xi[Zast1,2]);
}

この Stan のコードは下の図のようなグラフィカルモデルを考えることに相当する．


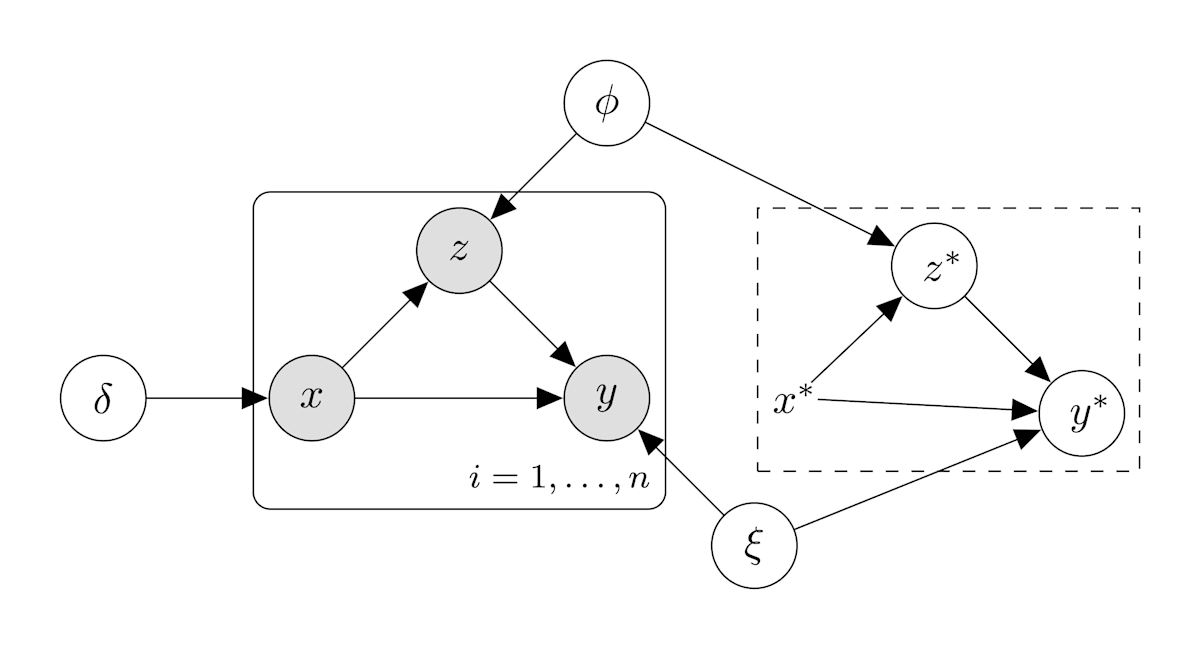
(2)の方針の確率的グラフィカルモデル2

「Xに効果があることがわかりました」という報告が「ただしここでいう効果はXを実際にやったときの効果ではありません」という意味だとすると，分析結果の使いみちに困る感じになる．

しかし，「z によって x が決まる」と順番まで仮定すると， x=a に固定したときに考える確率的グラフィカルモデルは (1) の場合に定まる．

「z によって x が決まる」ことを z \rightarrow x と書くことにすると，次のようなグラフが書け，これを因果グラフと呼ぶ．


z \rightarrow x のときの因果グラフ

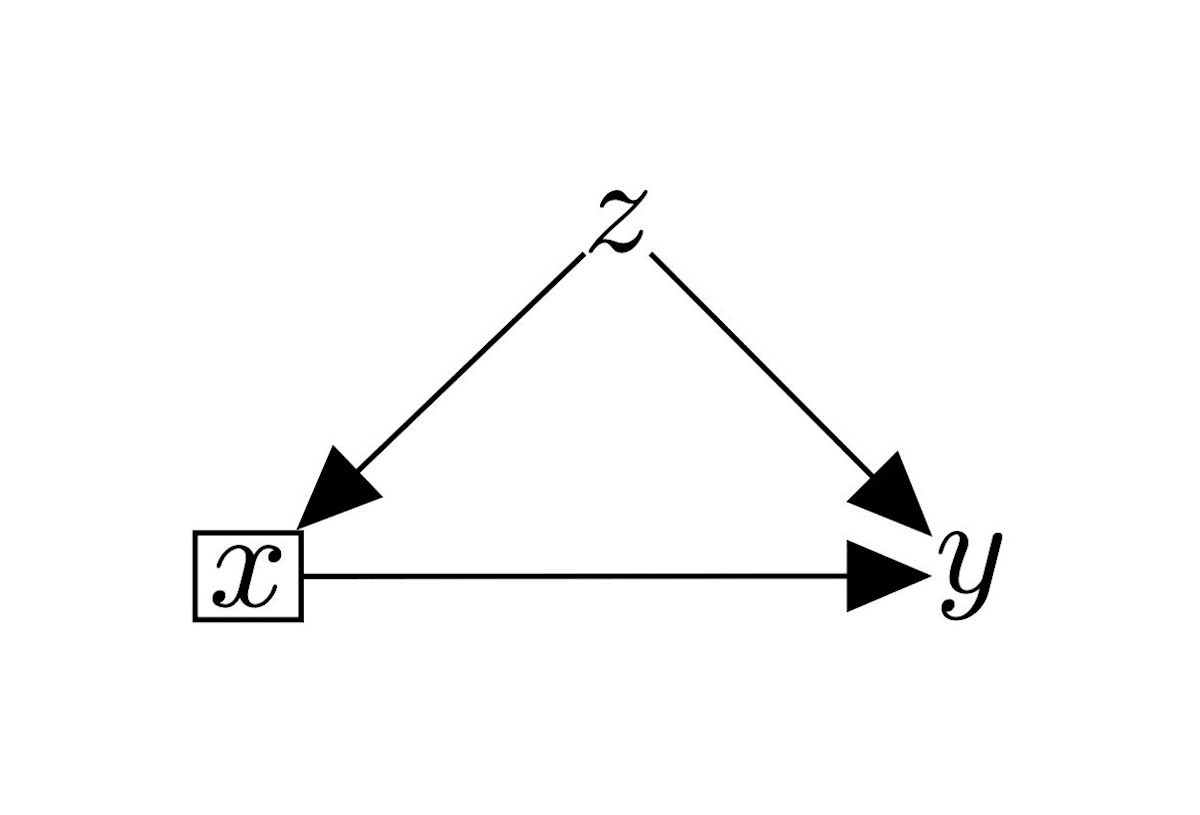
この図では do(\cdot) で固定する変数を四角で囲った．確率的グラフィカルモデルは介入についての仮定は入らない点が因果グラフと異なる．

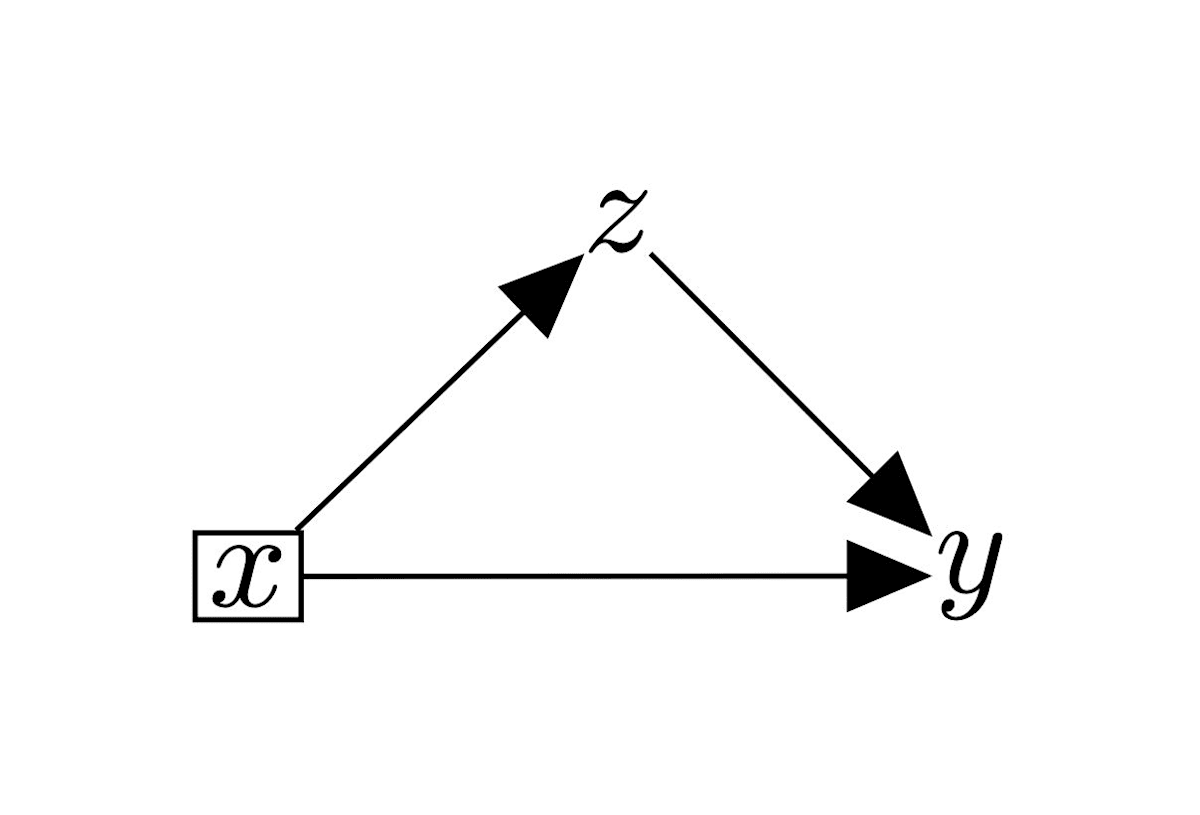
次のように因果グラフが与えられれば， x=a に固定したときに考える確率的グラフィカルモデルは (2) の場合に定まる．


x \rightarrow z のときの因果グラフ

逆に言うと，このように介入後のモデルを考えるために必要な仮定を「因果」と呼んでいることになるだろう．

上のような介入を行った場合まで含めた確率的グラフィカルモデルは因果グラフから機械的に得られる．すなわち do(x) で固定される x に入るパスをすべて除き，介入後と介入前の対応する変数どうしに共通のパラメータを置けばよい．

因果グラフが z \rightarrow x の場合の潜在結果変数の分布は，(1)の式から，

p(y^\ast|do(x=a)) = \sum_{z} p(y^\ast|z^\ast, do(x=a)) \cdot p(z^\ast)

ここでは x^\ast から z^\ast に伸びるパスがないから p(z^\ast) = p(z^\ast | do(x=a)) である．

因果グラフが x \rightarrow z の場合の潜在結果変数の分布は，(2)の式から，

p(y^\ast|do(x=a)) = \sum_{z} p(y^\ast|z^\ast,do(x=a)) \cdot p(z^\ast | do(x=a))

である．

潜在結果変数についての期待値 E[y(do(x=1))-y(do(x=0))]　を平均処置効果（average treatment effect; ATE）と呼ぶ．

真の分布の下での平均処置効果は R では次のように書ける．

因果グラフが z \rightarrow x のとき：

ATE_case1 = function(xi, psi, gamma){
  y0 = (1-gamma)*xi[1,1]+gamma*xi[2,1]
  y1 = (1-gamma)*xi[1,2]+gamma*xi[2,2]
  return(mean(y1-y0))
}

因果グラフが x \rightarrow z のとき：

ATE_case2 = function(xi,  phi, delta){
  y0 = phi[1]*xi[2,1] + (1-phi[1])*xi[1,1]
  y1 = phi[2]*xi[2,2] + (1-phi[2])*xi[1,2]
  return(mean(y1-y0))
}

平均処置効果の真値はそれぞれ次のようになる．

> print(round(ATE_case1(xi = Xi, psi=PX_z$p, gamma=PZ$p),3)) #D1
[1] 0.223
> print(round(ATE_case2(xi = Xi, phi=PZ_x$p, delta=PX$p),3)) #D2
[1] 0.008

Stan のコードで int D = Yast1-Yast0; のようにして，平均すれば平均処置効果の推定値が得られる．やってみた結果を下の表にまとめる．

variable mean sd
D1 (case1.stan) 0.16 0.60
D2 (case1.stan) -0.03 0.71
D1 (case2.stan) 0.15 0.61
D2 (case2.stan) -0.04 0.71

因果グラフが z \rightarrow x の場合の平均処置効果を D1，因果グラフが x \rightarrow z の場合の平均処置効果を D2 とした．case1.stan と case2.stan はどちらも近い分布が得られるが，因果グラフの違いは大きく結果に影響することがわかる．

さて，実はこの設定ではMCMCを用いる必要はなく，事後分布はベータ分布であり閉じた形で求まる．もちろん最尤法を用いてもいい．というか，通例は最尤法を用いた場合の具体的な計算の手順が層別解析のやり方として紹介されている．因果推論に関する本をお持ちの方は，目次を探して「層別」や「標準化」の章があればそれを参照してほしい．例えば，

などに解説がある．

ちなみに，『宇宙怪人しまりす統計よりも重要なことを学ぶ』では「層別解析」だとサブグループ解析などと混同しやすいことから，「層化統合解析」という用語を提案している．たしかにそのとおりだと思うので今後は「層化統合解析」の方を採用するかもしれない．今回はこの文章だけで完結するような書き方ではない （あまり self-contained でない）ので他の文献を参照しやすいよう，よく使われる「層別解析」を使用した．

感想など

統計的因果推論の必要性について

最初，因果グラフを与えた上でないと因果推論ができないのは物足りなく感じたことがある．
しかし，上の例のような因果効果の符号が逆とか，大きさが小さすぎとかの場面を想像すると，質的に因果関係がわかったとしても，量的な因果関係を知ることが重要と思えた．

一方で，大抵の場合は因果グラフも未知であり「モデル」である．因果的グラフィカルモデルを考えるときは，データの数字の部分だけでなくデータ取り方も重要になるだろうから，疫学の分野でよく言われる「コホート研究」や「ケースコントロール研究」などの観察研究の分類も，この観点から整理できるかもしれない．

因果的グラフィカルモデルについて意見がわかれるようなときも，仮定を明示したほうが「この部分がちょっと違った場合は……」のような議論がクリアになるだろう．

ついでに，「ちょっと違った」場合どの程度分析結果が変わりうるか，影響を量的に調べる感度分析というのも必要性があるだろう．

もう少し細かい話

数理統計の教科書では推定量のバイアス（bias）はパラメータ \theta とその推定量 \hat \theta の差 \theta - E[\hat{\theta}] と定義される．因果推論の文脈でバイアスを減らすことが強調される場合は，もう少し狭い意味でのバイアス——標本サイズを大きくしても小さくならないようなバイアス——と捉えるべきだろう．つまり不偏推定量を使わなくとも因果推論の目的に照らして矛盾はないだろう．

また，上で標準誤差を見たような場面でP値を見ることも因果推論の目的とはまったく対立しないだろう．

使用したコードなど

Stan のコードの全体は，case1.stan がこちら：

https://github.com/abikoushi/Zenn_content/blob/main/stan/stratified_stan/case1.stan

case2.stan がこちら：

https://github.com/abikoushi/Zenn_content/blob/main/stan/stratified_stan/case2.stan

R のコードの全体はこちら：

https://github.com/abikoushi/Zenn_content/blob/main/R/stratified_stan.R

グラフィカルモデルの図は TikZ で書いていて

https://github.com/abikoushi/Zenn_content/tree/main/tex/stratified_stan

のディレクトリにある．

GitHubで編集を提案

Discussion