VAEをEMでやってみる（EMアルゴリズムと変分ベイズ法の違い・実装編）

EMアルゴリズムと変分ベイズ法の違い

の続き…

上のリンク先で, 変分ベイズ法では

$$p(\theta, z|y) \approx q(\theta) q(z)$$

なる $q(\theta)$, $q(z)$ を求めるというようなことを書いた.

ニューラルネットワークを用いたVAE(Variational Auto-Encoder)の文脈では, ニューラルネットの係数パラメータ（上の式では$\theta$とおいた）に関しては点推定をして, サンプルごとに異なる潜在変数（上の式では$z$とおいた）を変分ベイズ法（ELBO最大化）で推定することが広く行われているようである.

この場合, ロス関数にエントロピー項があるかないかがEMアルゴリズムと変分ベイズ法の違いになるだろう.

実際, VAEのロス関数からエントロピー項をなくしたらどうなるかやってみよう.

Rのコードについては

schmons/torch_R_examples(GitHub)

をほぼそのまま使っているが, 少し変えたので記事の最後にまとめて貼っておきます.

VAEそのものについては他の文献を参照してほしい. 以下では最低限のことだけ説明する.

$q(z)$ は事後分布（データの情報が入った $z$ の分布）であるのでデータ $y$ の関数と見ることもできる.

VAEでは $q(z)$ のクラスを正規分布に制限し, 正規分布の平均 $\mu$ と分散 $\sigma^2$ をデータ自身の関数として, これをニューラルネットで作る.

VAEの文脈ではこの $q(z)$ をエンコーダー（encorder）と呼ぶことがある.

その場合, 「データ生成過程」の部分, すなわち $p(y|z,\theta)$ はデコーダー（decorder）と呼ばれる.

VAEのロス関数では, $z$ の事前分布は標準正規分布（平均0, 分散1）の直積として,

kl_div =  1 + log_var - mu$pow(2) - log_var$exp()
kl_div_sum = - 0.5 *kl_div$sum()

を足しているが, EMバージョンのVAE(この記事中ではEMAEと呼ぶことにする)は

musq = mu$pow(2)
musq_sum = 0.5 * musq$sum()

のみを足している（EMアルゴリズムと変分ベイズ法の違いで述べたように, 正規分布のエントロピーの部分を消している.）

さて, MNIST（0から9までの手書き文字のデータで機械学習の分野でよく使われる）を使ってVAEとEMAEを学習させてみよう.

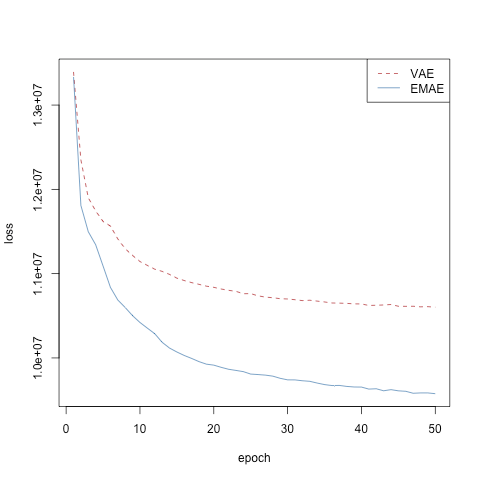
50エポックでロスはどちらも無事小さくなっている（まだ下がりきってる感じはしないが）.

標準正規分布からサンプリングした乱数で画像を作ってみる.

VAEによる結果：

EMAEによる結果：

VAEはいろんな数字らしきものができているが, EMAEでは”0”のようなものばかり出る.

潜在変数（今回は30次元とした）の平均 $\mu$ を部分的にプロットしてみる.

VAEの場合：

EMAEの場合：

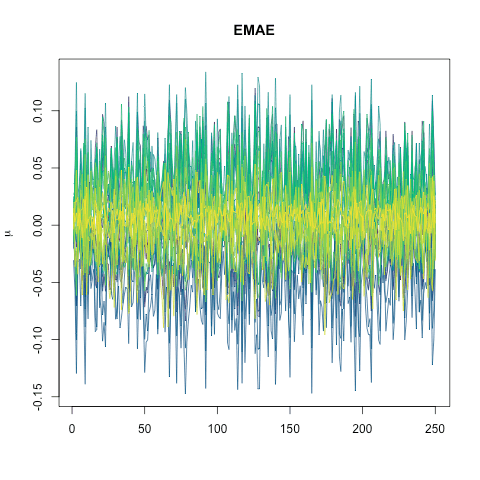
VAEのほうは特徴のある変数とほぼいつも0の変数がはっきり分かれている.

一方, EMAEでは30次元の潜在変数全体がまんべんなく少しづつ特徴を持っている感じになっている.

付録：Rのコード

library(torch)
library(luz)
library(torchvision)
library(dslabs)
#install_torch()
torch_tensor(1)

# このコードは下記をほぼそのまま使っています。
# Author: Sebastian Schmon, 2022
# browseURL("https://github.com/schmons/torch_R_examples")

# load MNIST
mnist <- read_mnist()
# Set VAEs latent dimension
latent_dim <- 30
# Define encoder and decoder network
encoder <- nn_module(
  "encoder",
  initialize = function(latent_dim) {
    # in_channels, out_channels, kernel_size, stride = 1, padding = 0
    self$conv1 <- nn_conv2d(1, 32, 3)
    self$conv2 <- nn_conv2d(32, 64, 3)
    self$dropout1 <- nn_dropout(0.25)
    self$dropout2 <- nn_dropout(0.5)
    self$fc1 <- nn_linear(9216, 128)
    self$fc2 <- nn_linear(128, latent_dim)
    self$fc3 <- nn_linear(128, latent_dim)
  },
  
  forward = function(x) {
    x %>% 
      self$conv1() %>%
      nnf_relu() %>%
      self$conv2() %>%
      nnf_relu() %>%
      nnf_max_pool2d(2) %>%
      self$dropout1() %>%
      torch_flatten(start_dim = 2) %>%
      self$fc1() %>%
      nnf_relu() %>%
      self$dropout2() %>%
      list(self$fc2(.), self$fc3(.))
  }
)

decoder <- nn_module(
  "decoder",
  initialize = function(latent_dim){
    self$fc1 <- nn_linear(latent_dim, 128)
    self$fc2 <- nn_linear(128, 128)
    self$conv1 <- nn_conv_transpose2d(128, 256, 1)
    self$conv2 <- nn_conv_transpose2d(256, 784, 1) 
  },
  forward = function(x) {
    x = self$fc1(x)
    x1 = nnf_relu(x)
    x2 = self$fc2(x1)
    x3 = nnf_relu(x2)
    x4 = torch_reshape(x3, list(x3$size(1), 64*2, 1, 1))
    x5 = self$conv1(x4)
    x6 = nnf_relu(x5)
    x7 = self$conv2(x6)
    x8 = torch_reshape(x7, list(x$size(1), -1))
    nnf_sigmoid(x8)
  }
)

# Define VAE model using encoder and decoder from above
vae_module <- nn_module(
  initialize = function(latent_dim=10) {
    self$latent_dim = latent_dim
    self$encoder <- encoder(latent_dim)
    self$decoder <- decoder(latent_dim)
  },
  forward = function(x) {
    f <- self$encoder(x)
    mu <- f[[2]]
    log_var <- f[[3]]
    z <- mu + torch_exp(log_var$mul(0.5))*torch_randn(c(dim(x)[1], self$latent_dim))
    reconst_x <- self$decoder(z)
    list(reconst_x, mu, log_var)
  }
)


mnist_dataset <- dataset(
  name = "mnist_dataset",
  initialize = function() {
    self$data <- self$mnist_data()
  },

  .getitem = function(index) {
    x <- self$data[index, ]
    x
  },
  
  .length = function() {
    self$data$size()[[1]]
  },
  
  mnist_data = function() {  
    input <- torch_tensor(mnist$train$images/255) 
    input
  }
)

#Initialize the VAE module with latent dimension as specified
vae <- vae_module(latent_dim=latent_dim)

# Dataloader
dl <- dataloader(mnist_dataset(), batch_size = 250, shuffle = TRUE, drop_last=TRUE)

# Optimizer. Note that a scheduler and/or a different learning rate could improve performance
optimizer <- optim_adam(vae$parameters, lr = 0.001)

epochs = 50  # Number of full epochs (passes through the dataset)

loss_history <- numeric(epochs)

# Optimization loop for VAE
for(epoch in 1:epochs) {
  l = 0
  coro::loop(for (b in dl) {  # loop over all minibatches for one epoch
    forward = vae(torch_reshape(b, list(b$size(1), 1, 28, 28)))
    #likelihood part of the loss
    loss = nn_bce_loss(reduction = "sum")
    mu = forward[[2]]
    log_var = forward[[3]]
    # KL part of the loss
    kl_div =  1 + log_var - mu$pow(2) - log_var$exp()
    kl_div_sum = - 0.5 *kl_div$sum()
    # Full loss
    output <- loss(forward[[1]], b) + kl_div_sum
    l = l + output
    optimizer$zero_grad()
    output$backward()
    optimizer$step()
  })
  loss_history[epoch] <- as_array(l)
  cat(sprintf("Loss at epoch %d: %1f\n", epoch, l))
}

###

#Initialize 
emae <- vae_module(latent_dim=latent_dim)
# Dataloader
dl <- dataloader(mnist_dataset(), batch_size = 250, shuffle = TRUE, drop_last=TRUE)

# Optimizer. Note that a scheduler and/or a different learning rate could improve performance
optimizer <- optim_adam(emae$parameters, lr = 0.001)

loss_history2 <- numeric(epochs)
# Optimization loop for EMAE
for(epoch in 1:epochs) {
  l = 0
  coro::loop(for (b in dl) {  # loop over all minibatches for one epoch
    forward = emae(torch_reshape(b, list(b$size(1), 1, 28, 28)))
    #likelihood part of the loss
    loss = nn_bce_loss(reduction = "sum")
    mu = forward[[2]]
    log_var = forward[[3]]
    # prior
    musq = mu$pow(2)
    musq_sum = 0.5 * musq$sum()
    # Full loss
    output <- loss(forward[[1]], b) + musq_sum
    #  
    l = l + output
    optimizer$zero_grad()
    output$backward()
    optimizer$step()
  })
  loss_history2[epoch] <- as_array(l)
  cat(sprintf("Loss at epoch %d: %1f\n", epoch, l))
}

png("loss_hist.png")
plot(loss_history, type = "l", col="firebrick", lty=2,
     ylim = range(loss_history, loss_history2), xlab="epoch", ylab="loss")
lines(loss_history2, type = "l", col="steelblue")
legend("topright",c("VAE","EMAE"),lty=2:1,col=c("firebrick","steelblue"))
dev.off()

# Generate new data
set.seed(1234)
png("vae_gen.png")
par(mfrow=c(4, 4), mai=c(0,0,0,0))
for(i in 1:16) {
  z = torch_randn(c(1, latent_dim))
  mat = torch_reshape(vae$decoder(z), list(28, 28))
  mat = matrix(as.numeric(mat), 28, 28)
  mat = apply(mat, 2, rev)
  image(t(mat), col = grey.colors(255), axes=FALSE)
}
dev.off()

set.seed(1234)
png("emae_gen.png")
par(mfrow=c(4, 4), mai=c(0,0,0,0))
for(i in 1:16) {
  z = torch_randn(c(1, latent_dim))
  mat = torch_reshape(emae$decoder(z), list(28, 28))
  mat = matrix(as.numeric(mat), 28, 28)
  mat = apply(mat, 2, rev)
  image(t(mat), col = grey.colors(255), axes=FALSE)
}
dev.off()

emae_forward = emae(torch_reshape(b, list(b$size(1), 1, 28, 28)))
vae_forward = vae(torch_reshape(b, list(b$size(1), 1, 28, 28)))

png("mu_EMAE.png")
matplot(as_array(emae_forward[[2]]),type="l",lty=1,col=hcl.colors(30),
        ylab=expression(mu), main="EMAE")
dev.off()

png("mu_VAE.png")
matplot(as_array(vae_forward[[2]]),type="l",lty=1,col=hcl.colors(30),
        ylab=expression(mu), main="VAE")
dev.off()