🙌

動的ハザードモデル（using Stan）

2024/01/05に公開

Stan

生存時間分析

tech

前置き

比例ハザードモデルの「比例」の部分を緩和する拡張はいくつか提案されている.（例えば Hemming, K., & Shaw, J. E. H. 2005. A class of parametric dynamic survival models. Lifetime data analysis, 11, 81-98.）が, あまり普及はしていない印象がある. その理由の一つは使いやすい実装が少ないせいかもしれない. Stanを使うとわりとかんたんに書ける.（といいつつも私は結構手こずったが…）

モデル

生存関数を $S(t)$ で表し, 離散時間でハザード $p_j$ を考える:

$p_1=1-S(t_1)$ ,
$p_2=\{S(t_1)-S(t_2)\}/S(t_1)$ ,
$p_3=\{S(t_2)-S(t_3)\}/S(t_2)$ ,
...

生存関数をハザードを使って書くと,

$S(t_1)=1-p_1$ ,
$S(t_2)=(1-p_2)S(t_1)$ ,
$S(t_3)=(1-p_3)S(t_2)$ ,
...

各時間区切りごとのイベント数を $y$ , リスクセット（その時間の直前までイベントの生起していない被験者数）を $R$ で表すと, ハザード $p_j$ に関する尤度は,

L_j \propto p_j^{y}(1-p_j)^{R-y}

と二項分布で書ける.

さらにハザード $p_j$ に対してロジットリンクで回帰構造を入れることを考える.

p_j = \begin{cases}\mathrm{logit}^{-1}(\alpha_j + \beta_j) & \text{(treat)}\\\mathrm{logit}^{-1}(\alpha_j + \beta_j) & \text{(control)} \end{cases}

$\alpha_j$ , $\beta_j$ に次の平滑化事前分布を設定する.

\alpha_j \sim \mathcal{N}(\alpha_{j-1}, \Delta_j \sigma^2),

\beta_j \sim \mathcal{N}(\beta_{j-1}, \Delta_j \sigma^2).

ここでは $\Delta_j = t_{j}-t_{j-1}$ .

以上では記号をやや曖昧に書いてしまったが、次のStanのコードを見て納得してほしい.

data{
  int<lower=1> N;
  int<lower=1> M;
  array[N] int<lower=0> Y;
  array[N] int<lower=0> R;
  array[N] int<lower=1,upper=M> time;
  array[N] real x;
  array[M] int<lower=1> delta;
}
parameters{
  array[M] real alpha;
  array[M] real beta;
  real<lower=0> sigma_a;
  real<lower=0> sigma_b;
}
model{
  for(i in 1:N){
   Y[i] ~ binomial_logit(R[i],alpha[time[i]]+beta[time[i]]*x[i]); 
  }
  for(i in 2:M){
    alpha[i] ~ normal(alpha[i-1], sqrt(delta[i])*sigma_a);
    beta[i] ~ normal(beta[i-1], sqrt(delta[i])*sigma_b);
  }
  beta[1] ~ normal(0,5);
  alpha[1] ~ normal(0,5);
  sigma_b ~ student_t(3,0,1);
  sigma_a ~ student_t(3,0,1);
}
generated quantities{
  vector[M] S1;
  vector[M] S2;
  S1[1] = 1-inv_logit(alpha[1]);
  S2[1] = 1-inv_logit(alpha[1]+beta[1]);
  for(i in 2:M){
    S1[i] = (1-inv_logit(alpha[i]))*S1[i-1];
    S2[i] = (1-inv_logit(alpha[i]+beta[i]))*S2[i-1];
  }
}

これをベースにして, 説明変数によって時間変化しない係数とする係数を使い分けるとか, 変化に制約をつけるとか（例えば単調であるとか）, いろいろ考えられると思う（ちゃんと推定できるかはやってみないとわからない）.

データ分析

R のパッケージ MASS に入っている Gehan データ（白血病についてのデータだったと思う）に対して, 生存関数を推定してみた.

生存関数をプロットしてみる. 帯は95%信用区間.

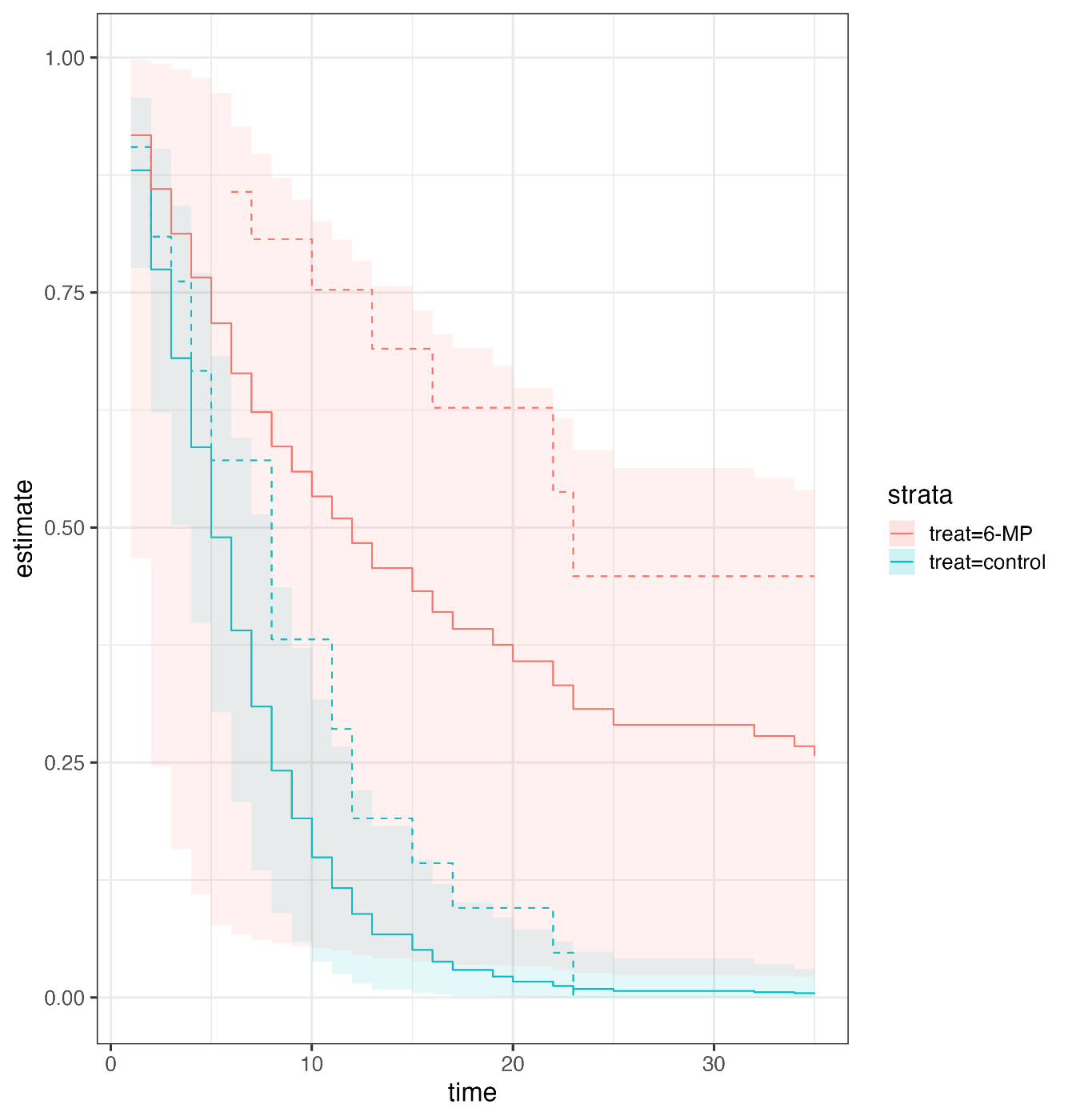
カプラン・マイヤー推定量（点線）と比較すると, このモデル（Stanで書いたほう）はあまり当てはまりが良くない気がする….

$\beta_j$ をプロットしてみる. 帯は95%信用区間.

6-MP（薬）投与群と, 対照群では明確に差が見て取れる.

以下、Rのコード:

library(cmdstanr)
library(posterior)
library(bayesplot)
library(survival)
library(dplyr)
library(ggplot2)
library(broom)
library(tidyr)
library(pammtools)
data(gehan, package="MASS")
sfit <- survfit(Surv(time,cens)~treat, data=gehan)
#plot(sfit)

ut <- unique(sort(gehan$time))

gehan2 <-gehan %>%
  group_by(time,treat) %>%
  summarise(Y=sum(cens),n=n()) %>% 
  group_by(treat) %>% 
  mutate(R=rev(cumsum(rev(n)))) %>% 
  ungroup() %>% 
  mutate(time2 = as.integer(factor(time)))
head(gehan2)

delta <- diff(c(0,ut))

stan_dat <- list(N = nrow(gehan2),
            Y = gehan2$Y,
            R = gehan2$R,
            M = n_distinct(gehan2$time2),
            time = gehan2$time2,
            delta = delta,
            x=gehan2$treat=="6-MP")
stan_dat
mod <- cmdstan_model("./Documents/dynamichazardmodel2.stan")
#args(mod$sample)
fit_mcmc <- mod$sample(
  data = stan_dat,
  seed = 1234,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 8000, iter_sampling = 2000)

mcmc_trace(fit_mcmc$draws(c("lp__","sigma_a","sigma_b","alpha[1]", "beta[1]")))+
  theme_bw()

M <- stan_dat$M
S1 <- apply(fit_mcmc$draws("S1"),3,mean)
S2 <- apply(fit_mcmc$draws("S2"),3,mean)

S1_ci <- t(apply(fit_mcmc$draws("S1"),3,quantile, prob=c(0.025,0.975)))
S2_ci <- t(apply(fit_mcmc$draws("S2"),3,quantile, prob=c(0.025,0.975)))

colnames(S1_ci) <- c("lower","upper")
colnames(S2_ci) <- c("lower","upper")

dfs <- tidy(sfit)
dfS1 <- data.frame(ut,S1,S1_ci)
dfS2 <- data.frame(ut,S2,S2_ci)
ggplot(dfs)+
  geom_step(aes(x=time,y=estimate,colour=strata), linetype=2)+
  geom_step(data = dfS1, aes(x=ut,y=S1,colour="treat=control"))+
  geom_stepribbon(data = dfS1, aes(x=ut,ymin=lower,ymax=upper,fill="treat=control"),alpha=0.1)+
  geom_step(data = dfS2, aes(x=ut,y=S2,colour="treat=6-MP"))+
  geom_stepribbon(data = dfS2, aes(x=ut,ymin=lower,ymax=upper,fill="treat=6-MP"),alpha=0.1)+
  theme_bw(16)+labs(fill="strata")

ggsave("surv.png")

b_ci <- t(apply(fit_mcmc$draws("beta"),3,quantile, prob=c(0.025,0.975)))
b_hat <- apply(fit_mcmc$draws("beta"),3,mean)
colnames(b_ci) <- c("lower","upper")

df_b <- data.frame(mean=b_hat, b_ci,time=ut)

ggplot(df_b)+
  geom_line(aes(x=time,y=mean), linetype=2)+
  geom_ribbon(aes(x=time,ymin=lower,ymax=upper),alpha=0.1)+
  theme_bw(16)
ggsave("beta.png")

前置き

モデル

データ分析

Discussion