項目反応理論で使われる2パラメータプロビットモデルのためのギブスサンプラーの実装例
Albert, J. H. (1992). Bayesian estimation of normal ogive item response curves using Gibbs sampling. Journal of educational statistics, 17(3), 251-269. https://www.jstor.org/stable/1165149 を参考にしていますがパラメータの置き方だけちょっといじっています.
モデルと分析対象
正解, 不正解の2値に明確に分類できるような試験問題を考えます.
被験者
この記事で扱う2パラメータ正規累積モデル(2PL normal ogive model)では, 被験者
とモデル化します.
潜在変数を用いた解釈
テストの背後には被験者
パフォーマンスが閾値0を超えた場合に正解にたどり着き, 0以下のとき誤答すると考えると,
正解の確率は,
不正解の確率は,
となり, 正規累積モデルの尤度と一致します.
識別パラメータ
ギブスサンプリング
ここから
事後分布の実現にギブスサンプリングを使います. ギブスサンプリングそのものについては別の文献を参照してください(例えば須山『ベイズ推論による機械学習入門』).
ここではギブスサンプリングのための full-conditional distribution だけ書きます.
潜在変数
これは正規分布の密度関数です.
これは正規分布の密度関数です.
これはガンマ分布の密度関数です.
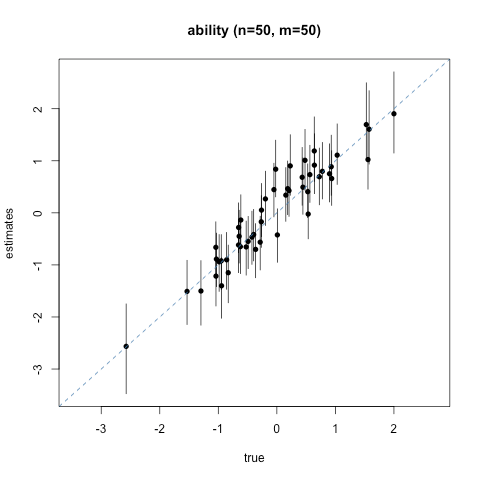
シミュレーション
モデルと同じ設定でデータを作ってちゃんと推定できるか確かめてみます.
100人に100問, 50人に100問, 100人に50問, 50人に50問と4通りの設定を試しました.
点が事後分布の平均, 縦の棒は95%信頼(信用)区間です.
ぴったり一致したときは図の対角線上に点が並びます.

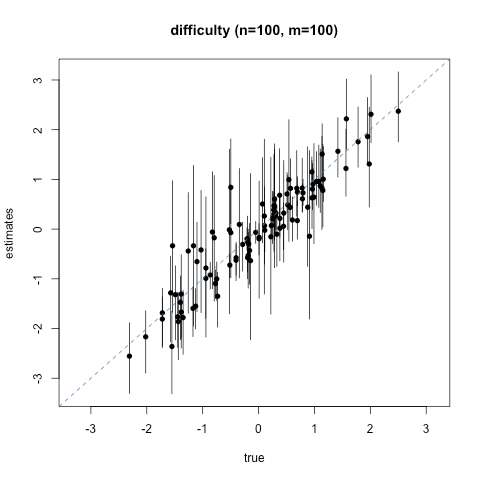




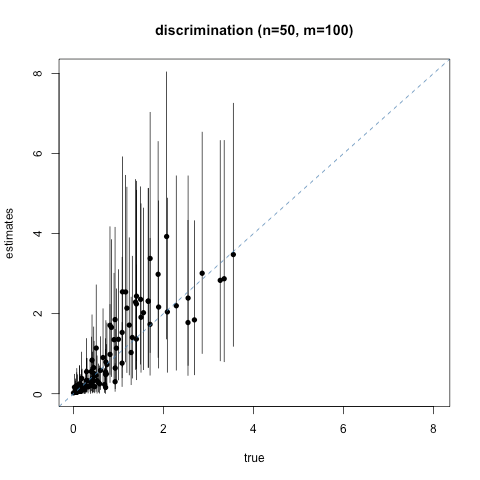
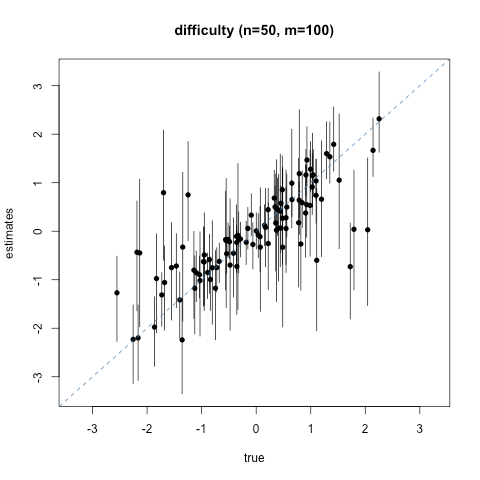

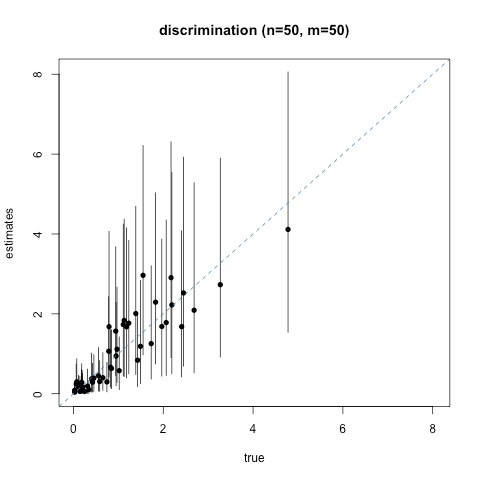

コード
#include <Rcpp.h>
using namespace Rcpp;
static const double t4 = 0.45;
/* Exponential rejection sampling (a,inf) */
double ers_a_inf(const double & a) {
double ainv = 1.0 / a;
double x;
double rho;
do {
x = R::rexp(ainv) + a; /* rexp works with 1/lambda */
rho = exp(-0.5 * pow((x - a), 2));
} while (R::runif(0, 1) > rho);
return x;
}
/* Normal rejection sampling (a,inf) */
double nrs_a_inf(const double & a) {
double x = -DBL_MAX;
while (x < a) {
x = R::rnorm(0, 1);
}
return x;
}
double rhalf_norm(const double & mean, const double & sd) {
const double alpha = (- mean) / sd;
if (alpha < t4) {
return mean + sd * nrs_a_inf(alpha);
} else {
return mean + sd * ers_a_inf(alpha);
}
}
/*
double rnorm_u (double eta, double sigma){
return R::qnorm(R::runif(R::pnorm(0,eta,sigma,true,false),1),eta,sigma,true,false);
}
double rnorm_l (double eta, double sigma){
return R::qnorm(R::runif(0,R::pnorm(0,eta,sigma,true,false)),eta,sigma,true,false);
}
*/
// [[Rcpp::export]]
List Gibbs2PLNO(int iter, IntegerMatrix y){
int n;
int m;
n = y.nrow();
m = y.ncol();
NumericMatrix theta(iter,n);
NumericMatrix gamma(iter,m);
NumericMatrix alpha(iter,m);
alpha(0,_) = rgamma(m,1,1);
NumericMatrix Z(n,m);
for(int k=1; k<iter; k++){
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
if(y(i,j)==1){
Z(i,j) = rhalf_norm((theta(k-1,i)-gamma(k-1,j)),1/sqrt(alpha(k-1,j)));
}else{
Z(i,j) = -rhalf_norm(-(theta(k-1,i)-gamma(k-1,j)),1/sqrt(alpha(k-1,j)));
}
}
}
for(int j=0; j<m; j++){
alpha(k,j) = R::rgamma(n/2.0+1,2.0/(sum(pow(Z(_,j)-(theta(k-1,_)-gamma(k-1,j)),2))+2));
gamma(k,j) = R::rnorm(sum(alpha(k,j)*(theta(k-1,_)-Z(_,j)))/(n*alpha(k,j)+1),1/sqrt(n*alpha(k,j)+1));
}
for(int i=0; i<n; i++){
theta(k,i) = R::rnorm(sum(alpha(k,_)*(Z(i,_)+gamma(k,_)))/(sum(alpha(k,_))+1),1/sqrt(sum(alpha(k,_))+1));
}
}
return List::create(Named("ability") = theta, _["item"]=gamma, _["alpha"]=alpha);
}
library(Rcpp)
library(parallel)
sourceCpp("albert1992.cpp")
Rhat <- function(samples_l){
samples <- simplify2array(samples_l)
term2 <-apply(apply(samples, 2:3, mean),1,var)
varW <-apply(apply(samples, 2:3, var),1,mean)
n.r <-nrow(samples)
var1 <-((n.r-1)/n.r)*varW+term2
sqrt(var1/varW)
}
quantile_mat <- function(x, probs=c(0.025, 0.975)){
t(apply(x[-burnin,,], 2, quantile, probs=probs))
}
compscattter <- function(true, estimates, intervals){
ran1 <-range(true, estimates, intervals)
plot(true, estimates, xlim=ran1, ylim=ran1, pch=16)
segments(true, intervals[,1], true, intervals[,2])
abline(0,1,lty=2, col="steelblue")
}
randbmat <- function(n,m){
theta <- rnorm(n,0,1)
gamma <- rnorm(m,0,1)
alpha <- rgamma(m,1,1)
y <- matrix(NA,n,m)
for(i in 1:n){
for(j in 1:m){
y[i,j] <- rbinom(1,1,pnorm(alpha[j]*(theta[i]-gamma[j])))
}
}
return(list(Y=y, theta=theta, gamma=gamma, alpha=alpha))
}
###
cond <- matrix(c(50, 50,
50, 100,
100, 50,
100, 100), byrow=TRUE, nrow = 4)
for(i in 1:4){
dat1 <- randbmat(cond[i,1], cond[i,2])
burnin <- 1:1000
fitlist <-mclapply(1:4,function(i){
Gibbs2PLNO(4000,dat1$Y)
},mc.cores = detectCores())
th <- simplify2array(lapply(fitlist, function(x)x$ability))
ga <- simplify2array(lapply(fitlist, function(x)x$item))
al <- simplify2array(lapply(fitlist, function(x)x$alpha))
#matplot(th[,2,], type = "l", lty=1, col=hcl.colors(4, alpha = 0.7))
print(all(Rhat(th[-burnin,,])<1.1))
print(all(Rhat(ga[-burnin,,])<1.1))
print(all(Rhat(al[-burnin,,])<1.1))
hattheta <-apply(th[-burnin,,],2,mean)
hatgamma <-apply(ga[-burnin,,],2,mean)
hatalpha <-apply(al[-burnin,,],2,mean)
cobntext <- paste0("(n=", cond[i,1], ", m=", cond[i, 2], ")")
png(paste0("abil_",i,".png"))
compscattter(dat1$theta,
apply(th[-burnin,,],2,mean),
quantile_mat(th[-burnin,,]))
title(paste("ability", cobntext))
dev.off()
png(paste0("diff_",i,".png"))
compscattter(dat1$ga,
apply(ga[-burnin,,],2,mean),
quantile_mat(ga[-burnin,,]))
title(paste("difficulty",cobntext))
dev.off()
png(paste0("disc_",i,".png"))
compscattter(dat1$alpha,
apply(al[-burnin,,],2,mean),
quantile_mat(al[-burnin,,]))
title(paste("discrimination", cobntext))
dev.off()
}
補足
Albert (1992) では
としていますがギブスサンプリングに使う条件付き分布の導出がちょっとだけ面倒になるので変えました.
Discussion