変分ベイズを使って変化点検知をしてみる の真似です.
ただし期間ごとのイベントの回数でなくイベントの起こった時点が得られているとしたところが違います.
モデルと推定量
イベントの発生時刻を t_i として、\Delta_i = t_i-t_{i-1} とする.
(i = 1, \ldots, N)
ただし t_0 は最初のイベントが生起した時点とする.
イベントから次のイベントまでの待ち時間は指数分布に従うとしたモデルを考える(こういうのをポアソン過程という).
\Delta_i \sim \mathrm{Exponential}(\lambda_i)
今回は
i<\tau のとき \lambda_i = \lambda^{(1)}
i\ge\tau のとき \lambda_i = \lambda^{(2)}
とする。
\tau の事前分布は離散一様分布とする.
\lambda^{(j)} (j=1,2) の事前分布はガンマ分布 \mathrm{Gamma}(a,b) とする.
i<\tau のとき1, i\ge\tau のとき0を取る変数 s_i を導入すると, 尤度 L は次のように書ける.
L = \prod_{i=1}^N \left\{ \lambda^{(1)} \exp(-\Delta_i \lambda^{(1)}) \right\}^{s_i}\left\{ \lambda^{(2)} \exp(-\Delta_i \lambda^{(2)}) \right\}^{1-s_i}.
対数をとると,
\log L = \sum_{i=1}^N \left\{ \lambda^{(1)} \exp(-\Delta_i \lambda^{(1)}) \right\}^{s_i}\left\{ \lambda^{(2)} \exp(-\Delta_i \lambda^{(2)}) \right\}^{1-s_i}.
これを s=(s_1,\ldots,s_N)' に関して整理することにより s の変分事後分布として次の q(s) が得られる.
q(s) = \prod_{i=1}^N \rho_i ^ {s_i},
ここでは E[~] を変分事後分布による期待値を取る操作とし,
\rho_i \propto \exp \left( \left\{\sum_{k=1}^{i} E[ \log \lambda^{(1)}] - \Delta_i E[\lambda^{(1)}] \right\} + \left\{\sum_{k={i+1}}^{N} E[\log \lambda^{(2)}] - \Delta_i E[\lambda^{(2)}] \right\}\right)
とした. また \lambda^{(j)} に関して整理することにより \lambda^{(j)} の変分事後分布として次の q(\lambda^{(j)}) が得られる.
q(\lambda_j) = \mathrm{Gamma}(\hat a_j, \hat b_j)
ここで
\hat a_1 = \sum_{i=1}^N E[s_i] + a
\hat b_1 = \sum_{i=1}^N E[s_i] \Delta_i + b
\hat a_2 = \sum_{i=1}^N E[(1-s_i)] + a
\hat b_2 = \sum_{i=1}^N E[(1-s_i)]\Delta_i +b
である.
coal データの分析
R の boot パッケージに炭鉱の事故の日付を記録したデータがある.
事故の累積発生回数をプロットしたもの:
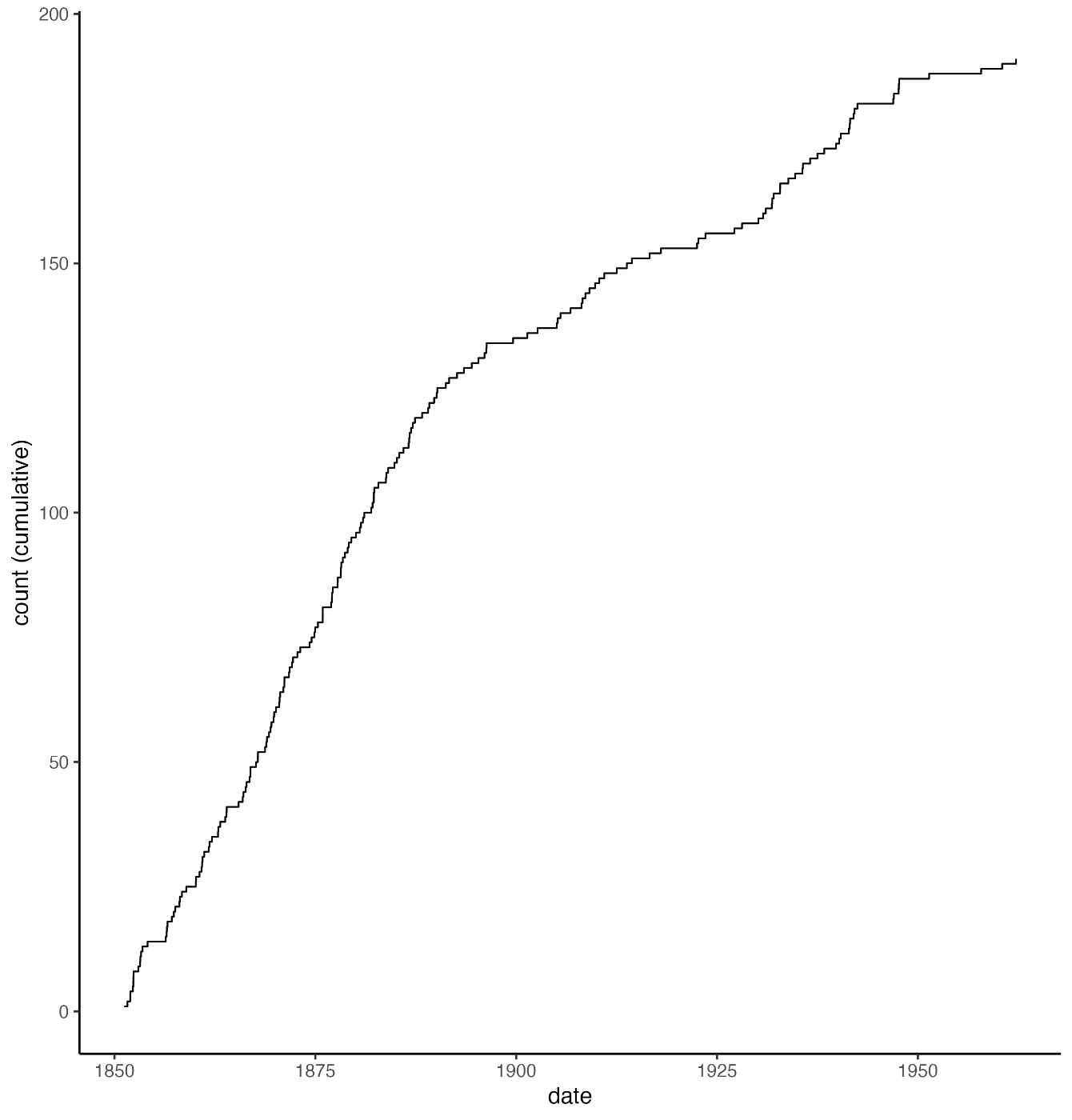
事故の発生回数をヒストグラムにしたもの:
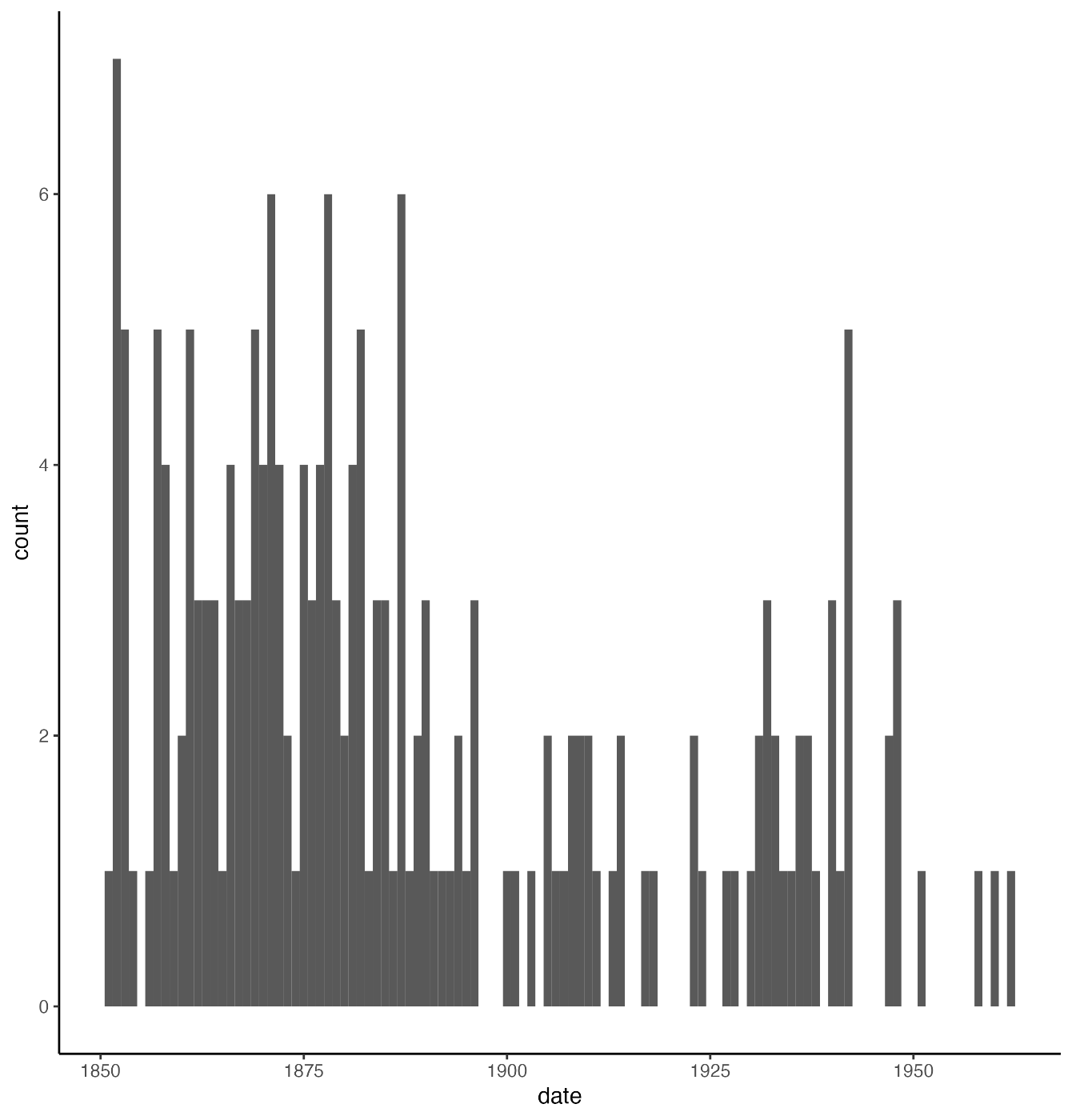
1900年前後を境に事故が減っているのがわかると思う.
上で求めた変分事後分布から200個疑似乱数でサンプリングしてグラフに重ねてみる.
事故の累積発生回数をプロットしたもの:
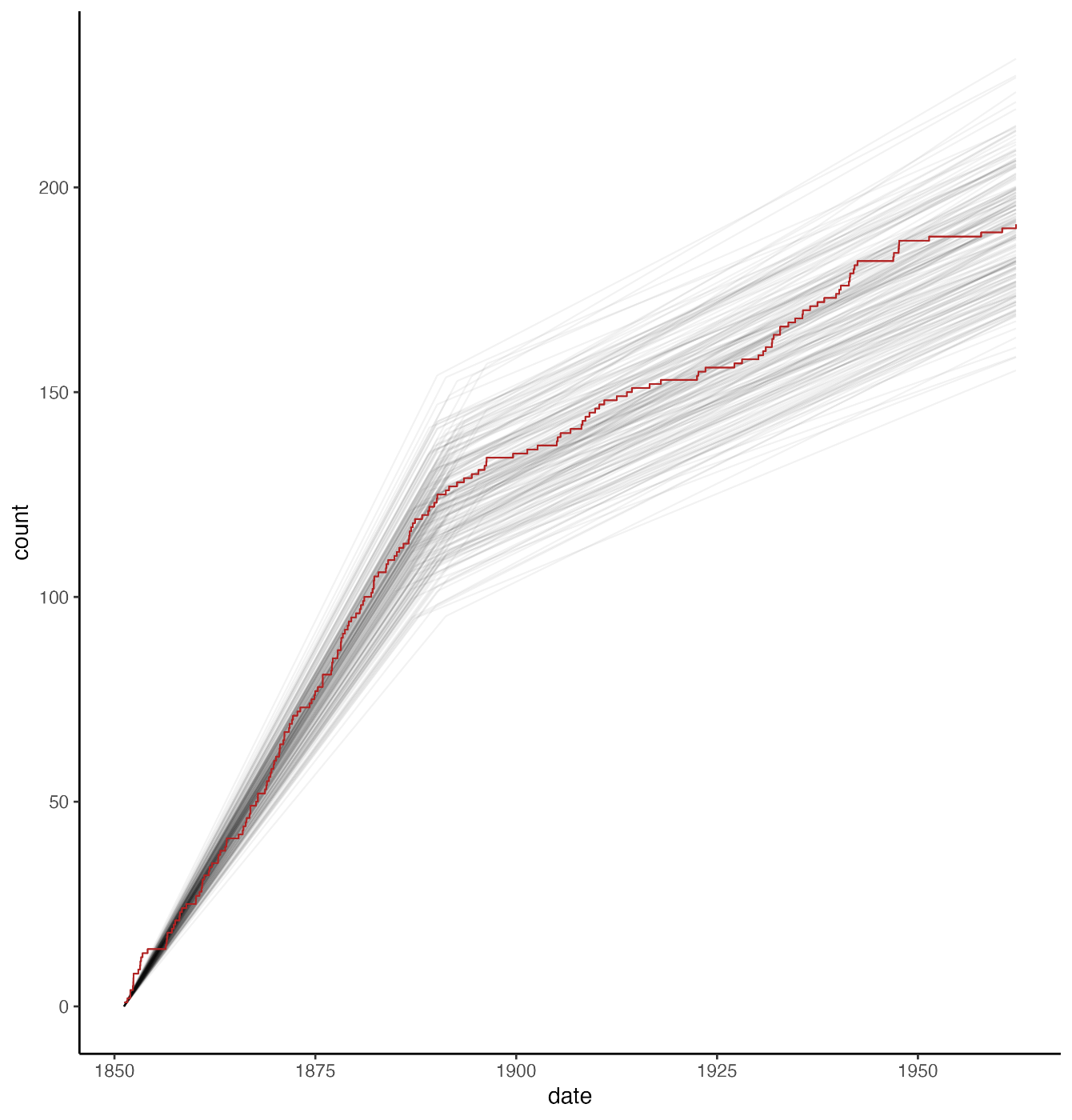
事故の発生回数をヒストグラムにしたもの:
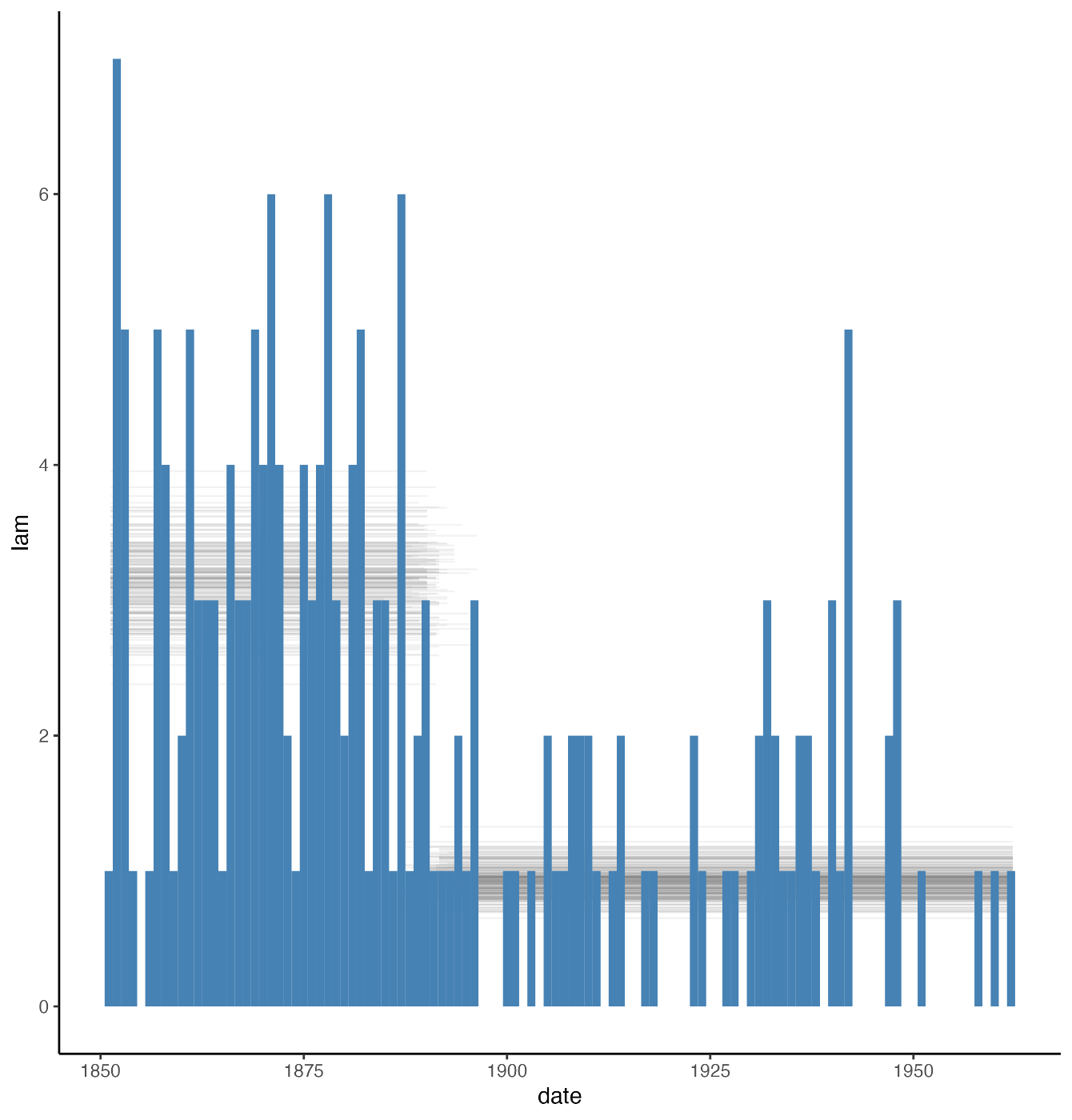
R のコードはこちら:
ちょっと変わってるのは cumsum_r という関数を定義してるところで, これは配列の末尾から累積和を取っています.
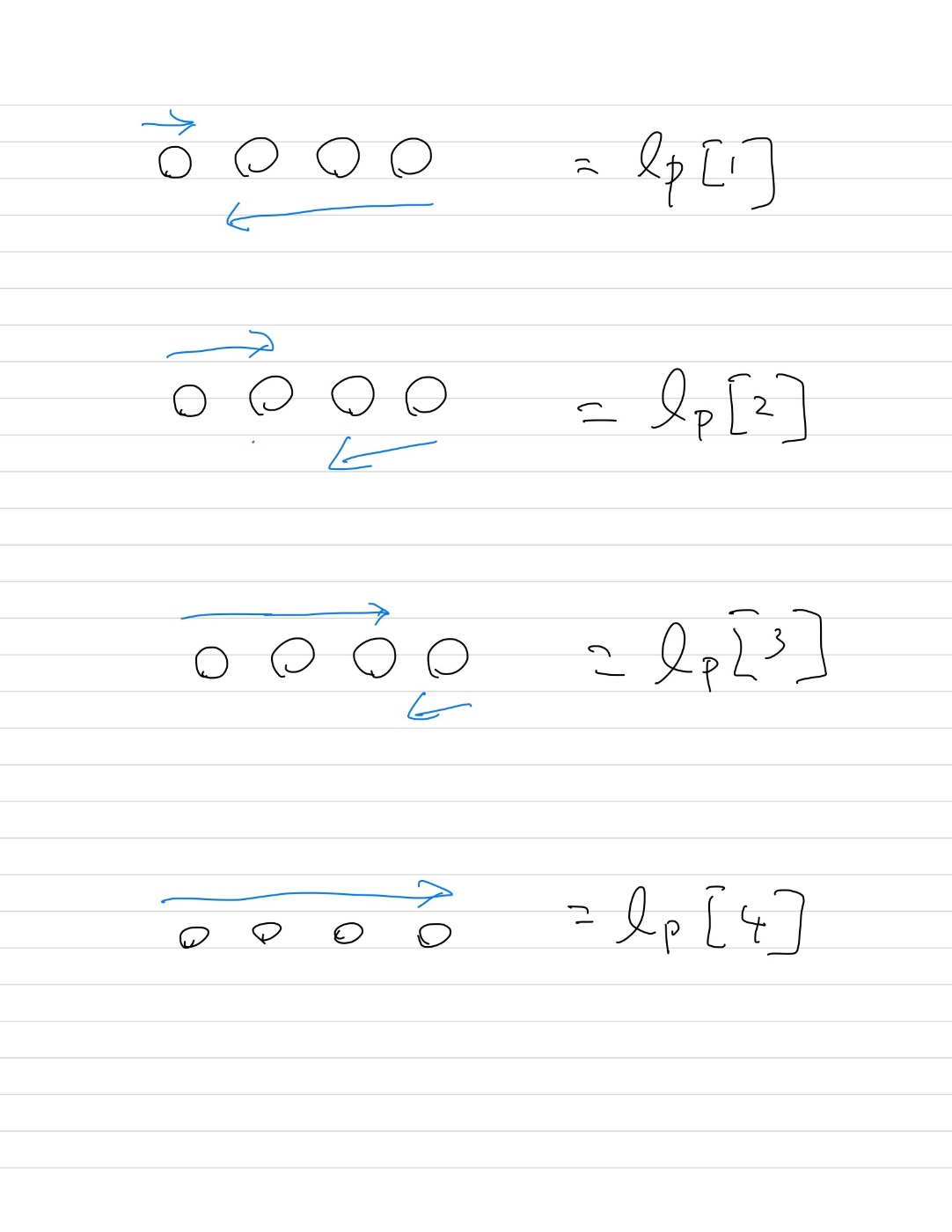
累積和を使って計算の無駄を省く(変化点検出の例)
を参考にしました.
ガンマ分布どうしのカルバック・ライブラー情報量は
Kullback–Leibler divergence between two gamma distributions
のwhuber氏のものをそのまま使っています.



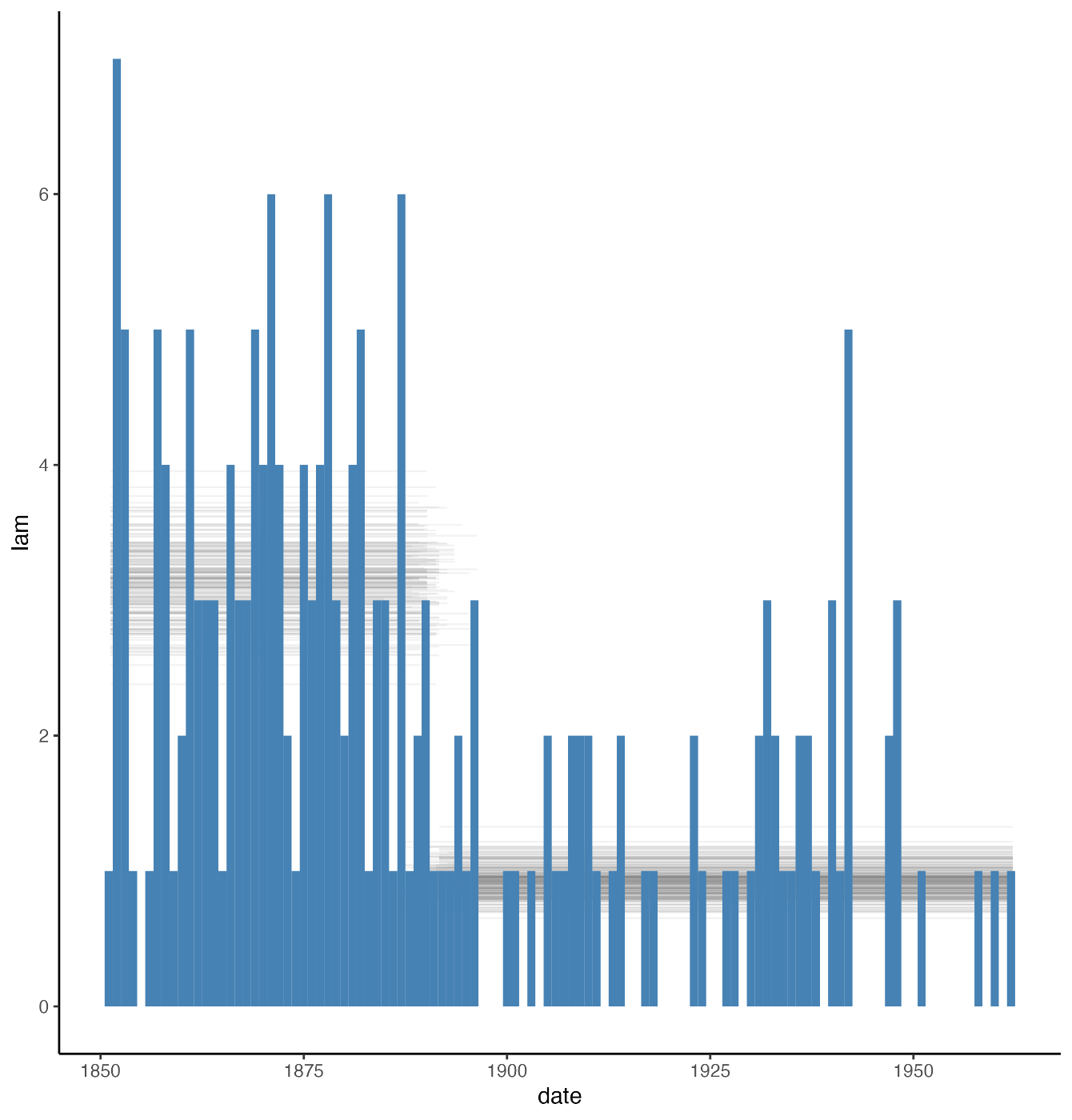
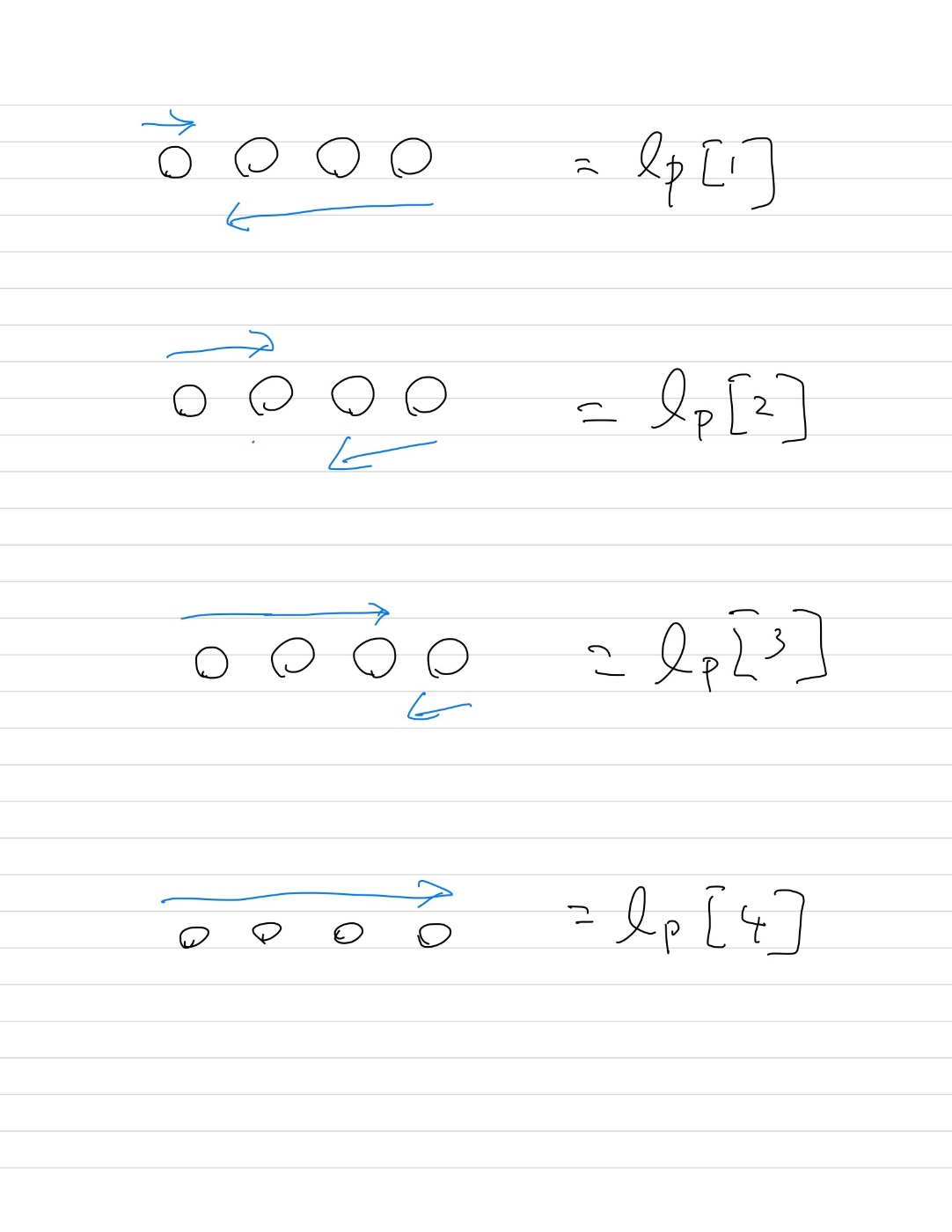


Discussion