ロジスティック回帰を経由して2×2の分割表のオッズ比の検定を作る

モチベーション

なぜわざわざそんなことをするのか？

• 最近は機械学習の手法としてロジスティック回帰を学んだことはあるが分割表の独立性の検定は知らないみたいな人もそこそこいるだろうし, 既知のことから発展して色々できたほうが楽で良いと思ったから
• わざわざしなくてもいいようなことをしたいときもあるから

モデル：ロジスティック回帰

ジスティック回帰は説明変数 $x_i$ を所与として, 次の二項分布を考える.

$$y_i \sim \mathrm{Binomial}(n_i, \mathrm{logit}^{-1}(\alpha + \beta x_i)),$$

ここで, $\mathrm{logit}^{-1}$ は逆ロジット変換

$$\mathrm{logit}^{-1}(x) = 1/(1+\exp(-x))$$

である. また, 今回は特に2×2の分割表のみを考えたいため, $x_i$ の取りうる値は0または1とする.

上の分布の $x_i$, $y_i$ についてクロス集計すると次のような分割表を考えることができる.

	$y=0$	$y=1$
$x=0$	$n_{00}$	$n_{01}$
$x=1$	$n_{10}$	$n_{11}$

分割表のオッズ比の検定

上と同じ記号のもとで $\exp(\beta)$ をオッズ比と呼ぶ.

$$1-\mathrm{logit}^{-1}(x) = \exp(-x)/(1+\exp(-x))$$

であり,

$$\mathrm{logit}^{-1}(x) / (1-\mathrm{logit}^{-1}(x)) = \exp(x)$$

であり,

$$\mathrm{logit}^{-1}(\alpha + \beta x_i) = \begin{cases} \mathrm{logit}^{-1}(\alpha) & x_i = 0\\ \mathrm{logit}^{-1}(\alpha + \beta) & x_i = 1 \end{cases}$$

であるから, 「$x_i = 1$ のときの $y_i=1$ が出る確率と $y_i=0$ が出る確率の比」と「$x_i =01$ のときの $y_i=1$ が出る確率と $y_i=0$ が出る確率の比」の比がオッズ比である.

このオッズ比に対して帰無仮説 $\beta = \beta_0$ の検定を作るには, 通例は2×2の分割表に対してポアソン分布の直積を考え, セルごとの分散が

$$Var(n_{ij}) = \lambda_{ij} \quad (i \in \{0,1\},~ j \in \{0,1\})$$

であるとして,

$$\frac{d}{d \lambda} \log \lambda = 1/\lambda$$

より, $\log n_{ij}$ の分散を $1/\lambda_{ij}^2 \cdot \lambda_{ij} = 1/\lambda_{ij}$ で近似）して（デルタ法 a.k.a 一次近似！）

$$Var(\log \{ (n_{11}/n_{10})/(n_{01}/n_{00}) \}) = \sum_{i,j} 1/(\lambda_{ij})$$

とすることにより求める. 真の $\lambda_{ij}$ は不明なので（それがわかっていたら研究することはないので） $\lambda = n_{ij}$ をプラグインする.

すなわち, オッズ比の対数の点推定量を $\hat \beta = \log \{ (n_{11}/n_{10})/(n_{01}/n_{00}) \}$, その標準誤差（推定量の標準偏差のこと）を $se(\hat \beta) = \sqrt{\sum_{i,j} 1/(n_{ij})}$ として,

$$(\hat \beta -\beta_0)/se(\hat \beta)$$

を標準正規分布で近似して棄却域を求める.

ずいぶん粗い近似が出てくるように思うかもしれないが, その感覚はたぶん正しい. 統計学はサンプルサイズが大きいときに一致させたいという気持ちがあるのでテイラー展開（後ろのほうは $1/n$ より速いオーダーで0に近づくので無視）と大数の法則, 中心極限定理の組み合わせをよく使う.

それが有限の現実的なサンプルサイズでうまくいくかというのは計算が難しく, シミュレーションに頼らざるを得ないことが多い.

ロジスティック回帰経由の分割表のオッズ比の検定

$x_i = 0$ のときの $y_i=1$ が出る確率を

$$p_0 = \mathrm{logit}^{-1}(\alpha)$$

$x_i = 1$ のときの $y_i=1$ が出る確率を

$$p_1 = \mathrm{logit}^{-1}(\alpha + \beta)$$

と置く.

$p_i$ ($i=0,1$) の最尤推定量は

$$\hat p_i = n_{i1}/(n_{i0}+n_{i1})$$

であり,

$$\log (p_0 /(1-p_0)) = \alpha,$$

$$\log (p_1 /(1-p_1)) = \alpha + \beta$$

であるから, 最尤推定量は変数変換に対して不変なので,

$$\hat \alpha = \log(n_{01}/n_{00}),$$

$$\hat \beta = \log(n_{11}/n_{10}) - \log(n_{01}/n_{00})$$

が得られる.

また

$$\frac{d}{dp_0} \alpha = 1/\{p_0(1-p_0)\}$$

から

$$\frac{d}{d\alpha} p_0 = p_0(1-p_0)$$

であるため, 二項分布の分散よりデルタ法では

$$Var(\hat \alpha) \approx \frac{1}{(n_{00}+n_{10})p_0(1-p_0)}$$

と近似できる.

$p_i$ に $\hat p_i$ を代入すると,

$$Var(\hat \alpha) \approx \frac{1}{n_{00}} + \frac{1}{n_{10}}$$

となる.

$\hat \beta$ も同様に計算して分散の加法性を使うと前節と同じ結果が得られる.

ちなみに

Stan Lipovetsky, Analytical closed-form solution for binary logit regression by categorical predictors. Journal of Applied Statistics, 2015.

でも同様の議論がなされている.

シミュレーション

カイ2乗分布とt分布を使った場合とでαエラーと検出力をシミュレーションしてみる.

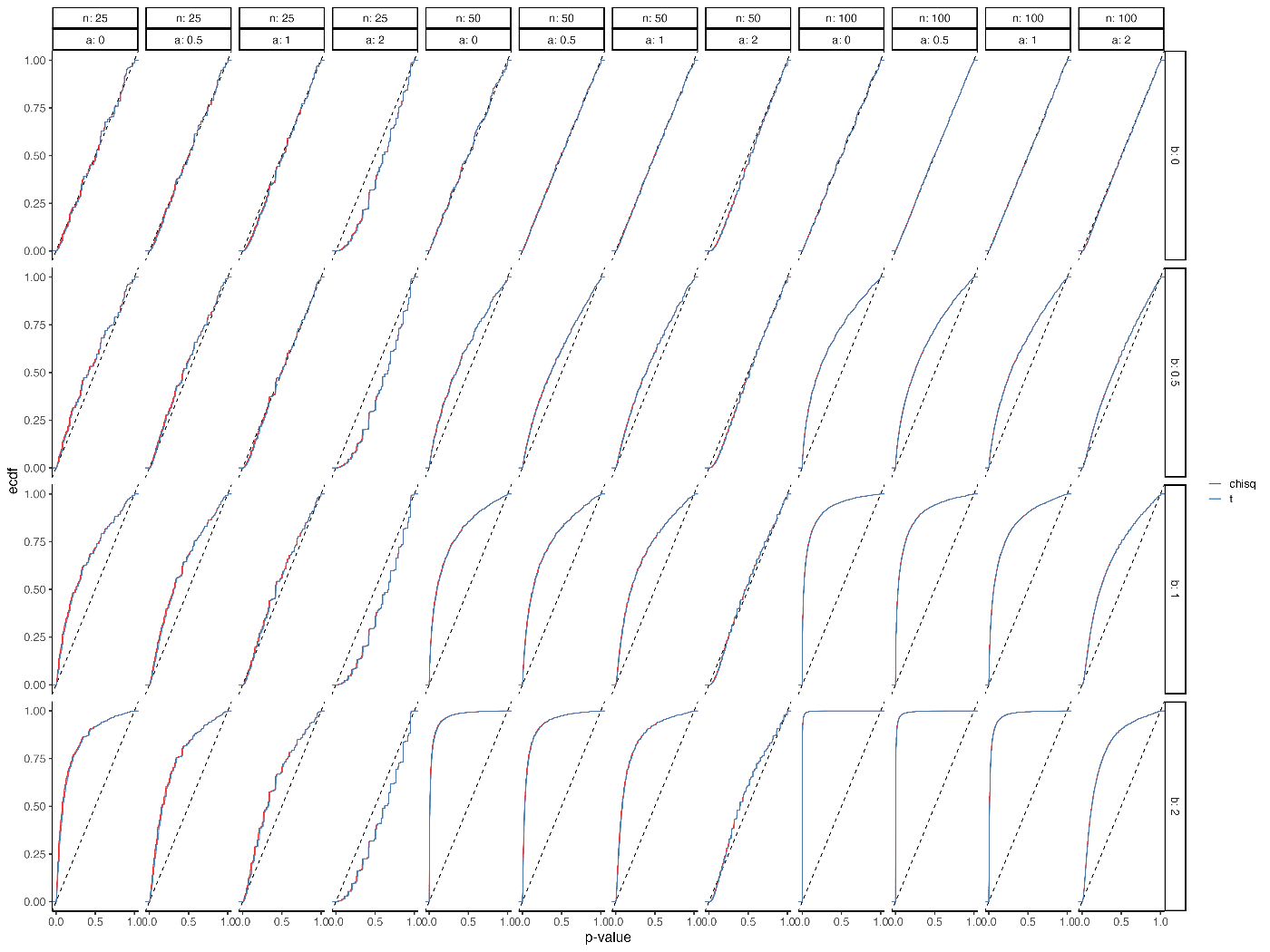
図の b=0 となっている行がαエラーで, どちらもほぼ名目上水準を達成していることがわかる.

違いはほとんどないが, 少しだけt統計量のほうが保守的である.

a ($\alpha$) が大きいとき（標本サイズが偏っていて一方が小さいとき）検出力が有意水準を下回ってしまっている点には注意が必要かもしれない. これはp値を一様分布でランダムに決めた場合より検出力が低いということである. こういうのをバイアスのある検定と呼ぶ.

R のコード

library(tidyr)
library(dplyr)
library(tibble)
library(ggplot2)

simOR <- function(i, n, a, b, beta0=0){
  set.seed(i)
  x <- rbinom(n, 1, 0.5)
  y <- rbinom(n, 1, plogis(a+b*x))
  x <- factor(x, levels = 0:1)
  y <- factor(y, levels = 0:1)
  tab <- table(x, y)
  beta <- log(tab[2,2])-log(tab[2,1]) - (log(tab[1,2])-log(tab[1,1]))
  se <- sqrt(sum(1/tab))
  return((beta-beta0)/se)
}

cond <- as.matrix(expand.grid(n=c(25,50,100), 
                    a=c(0,0.5,1,2),
                    b=c(0,0.5,1,2)))
conddf <- as.data.frame(cond) %>% 
  rowid_to_column()
res <- apply(cond, 1, function(par)sapply(1:10000, simOR, n=par[1], a=par[2], b=par[3]))
resdf <- pivot_longer(as.data.frame(res), 1:48, names_to = "rowid") %>% 
  mutate(rowid = as.integer(gsub("V","",rowid))) %>% 
  left_join(conddf, by="rowid")

ggplot(resdf)+
  geom_abline(slope=1, intercept = 0, linetype=2)+
  stat_ecdf(aes(x=pchisq(value^2, df=1, lower.tail=FALSE), colour="chisq"), alpha=0.9)+
  stat_ecdf(aes(x=2*pt(abs(value), df=n-2, lower.tail=FALSE), colour="t"), alpha=0.9)+
  scale_colour_brewer(palette = "Set1")+
  facet_grid(b~n+a, labeller = label_both)+
  labs(x="p-value", colour="")+
  scale_x_continuous(breaks = seq(0,1,length.out=3))+
  theme_classic(16)
ggsave("p_or1.png", width = 20, height = 15)