拡散方程式
次の偏微分方程式を一次元の拡散方程式と呼ぶ:
\frac{\partial}{\partial t} u(t,x) = a \frac{\partial}{\partial x^2} u(t,x)
ここで u(x, t) は位置 x, 時点 t における考えたい対象の物の濃度とした.
a は拡散係数と呼ばれる定数で a > 0 である.
拡散方程式を離散化して u_{tx} (t=0,1, \ldots ,m, x=1, \ldots ,n) について次の差分方程式を考える.
\begin{aligned}
u_{t+1,x}-u_{t,x} &= a ( u_{t,x+1}-u_{t,x} - (u_{t,x}-u_{t,x-1}) )\\
&=a ( u_{t,x+1}-2u_{t,x}+u_{t,x-1}) )\tag{1}
\end{aligned}
添字がtの変数を全部右辺に, t+1の変数が全部左辺にくるように書き換えると時点tの状態(現在)から次のt+1での状態(未来)がわかって便利である:
\begin{aligned}
u_{t+1,x} &= u_{t,x} + a ( u_{t,x+1}-2u_{t,x}+u_{t,x-1}) )\\
&= (1-2a)u_{t,x} + a u_{t,x+1} + au{t,x-1}
\end{aligned}
u_t=(u_{t,1}, \ldots , u_{t,n})' とまとめると, 次のように行列を使って書くこともできる:
u_{t+1} = \begin{pmatrix}
\ddots& & & &\\
& 1-2a & 0 & 0& \\
&a & 1-2a & 0&\\
&0 & a & 1-2a & \\
& & & & \ddots\\
\end{pmatrix} u_t. \tag{1'}
ところで, (1) では時間についての差分として u_{t+1,x}-u_{t,x} を考えた.
時間についての差分として u_{t,x}-u_{t-1,x} を考えることにすると,
u_{t,x}-u_{t-1,x} = a ( u_{t,x+1}-2u_{t,x}+u_{t,x-1}) ) \tag{2}
より
\begin{aligned}
u_{t-1,x} &= u_{t,x} - a ( u_{t,x+1}-2u_{t,x}+u_{t,x-1}) )\\
&= (1+2a)u_{t,x} - a u_{t,x+1} - au{t,x-1}
\end{aligned}
という方程式を導くこともできる.
(1') と同様に行列を使って
u_{t-1} = \begin{pmatrix}
\ddots & & & & \\
& 1+2a & 0 & 0 & \\
& -a & 1+2a & 0 & \\
& 0 & -a & 1+2a & \\
& & & & \ddots\\
\end{pmatrix} u_t
書くことができる.
添字がtの変数を全部右辺に, t+1の変数が全部左辺にくるように書き換えると
u_{t} = \begin{pmatrix}
\ddots & & & & \\
& 1+2a & 0 & 0 & \\
& -a & 1+2a & 0 & \\
& 0 & -a & 1+2a & \\
& & & & \ddots\\
\end{pmatrix} ^{-1} u_{t}. \tag{2'}
が得られる.
さて, 以上では実は考えている空間の端っこ(u_{t,1} と u_{t,n})で2階差分が定義されていなかった.
端っこでは物の出入りがないとして
とする(偏微分方程式でいう境界条件に対応する)と(1)は次のようになる:
\begin{aligned}
u_{t+1,1}-u_{t,1} &= a (u_{t,2}-u_{t,1})\\
u_{t+1,1} &= (1-a)u_{t,1}+a u_{t,2}
\end{aligned}
u_{t+1,n} についても同様の計算をしてまとめると次を得る:
行列 A は
\begin{aligned}
A=\begin{pmatrix}
1-a & a & 0 & 0 & \cdots & 0 & 0 & 0\\
a & 1-2a & a & 0 & \cdots &0 & 0 & 0\\
0 & a & 1-2a & a & \cdots &0 & 0 & 0\\
\vdots &\vdots &\vdots &\vdots & \ddots & \vdots &\vdots &\vdots\\
0 & 0 & 0 & 0 & \cdots & 1-2a & a & 0\\
0 & 0 & 0 & 0 & \cdots & a & 1-2a & a\\
0 & 0 & 0 & 0 & \cdots & 0 & a & 1-a \\
\end{pmatrix}.
\end{aligned}
とした.
(2')は次のように書ける:
u_{t+1} = A^{-1}u_t \tag{2''}
ここで行列 A は
\begin{aligned}
A=\begin{pmatrix}
1+a & -a & 0 & 0 & \cdots & 0 & 0 & 0\\
-a & 1+2a & -a & 0 & \cdots &0 & 0 & 0\\
0 & -a & 1+2a & -a & \cdots &0 & 0 & 0\\
\vdots &\vdots &\vdots &\vdots & \ddots & \vdots &\vdots &\vdots\\
0 & 0 & 0 & 0 & \cdots & 1+2a & -a & 0\\
0 & 0 & 0 & 0 & \cdots & -a & 1+2a & -a\\
0 & 0 & 0 & 0 & \cdots & 0 & -a & 1+a \\
\end{pmatrix},
\end{aligned}
とした.
(1'')のやり方を(拡散方程式の数値解法で更新式が陽に書けるので)陽解法, (2'')のやり方を陰解法みたいに呼ぶこともある. 以降, この記事でもこの呼び方を使う.
Rによる計算例(ノイズなし)
初期条件は次のように与えた:
u_ini = numeric(20)
u_ini[c(3:5,8:10,15:16)] = 1
陽解法はほぼ(1'')の式通りで, 行列 A を次のように作り, for 文で繰り返しかけていく.
A <- diag(1-2*r,n)
A[cbind(2:n,1:(n-1))] <- r
A[cbind(1:(n-1),2:n)] <- r
A[1,1] = 1-r
A[n,n] = 1-r
陰解法は(2'')の式通り愚直に実装すると逆行列が出てきてしまうが, 今回はそのまま愚直にsolve関数を使って実装した.
A <- diag(1+2*r,n)
A[cbind(2:n,1:(n-1))] <- -r
A[cbind(1:(n-1),2:n)] <- -r
A[1,1] = 1+r
A[n,n] = 1+r
A <- solve(A)
拡散係数 a=0.2 として陽解法による結果:
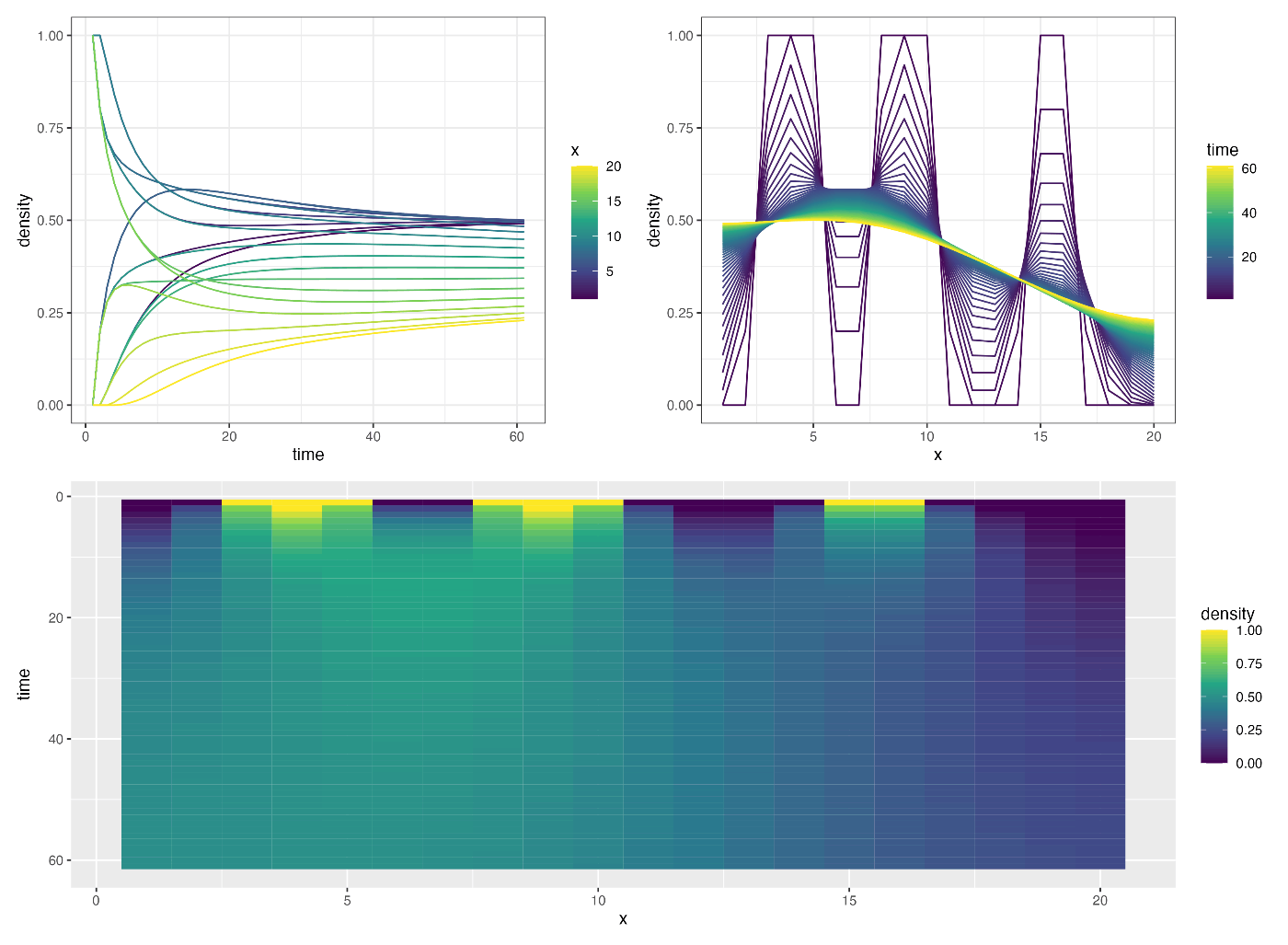
この図(3つ)は全部同じ対象 u_{x,t} をプロットしている. time t, x が x, density が u_{x,t}.
(自分のイメージとしては細長い水槽に何か所か同時にインクを入れて広がって行く様子を見てるみたいな感じです.)
拡散係数 a=0.2 として陰解法による結果:
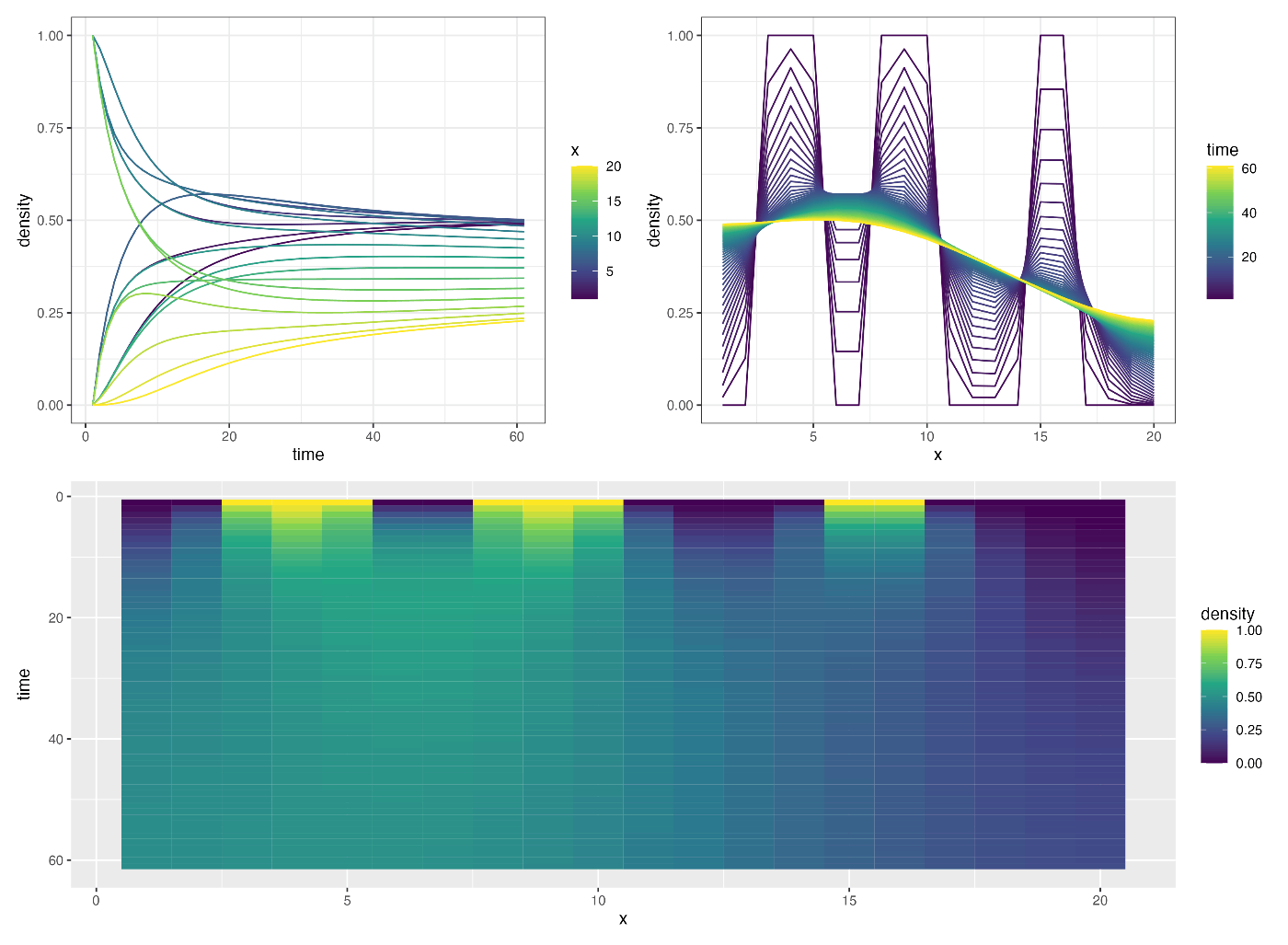
ぱっと見では区別がつかないくらい似たような値が得られている.
ので, 比較のため x ごとに同じパネルにプロットしてみる:
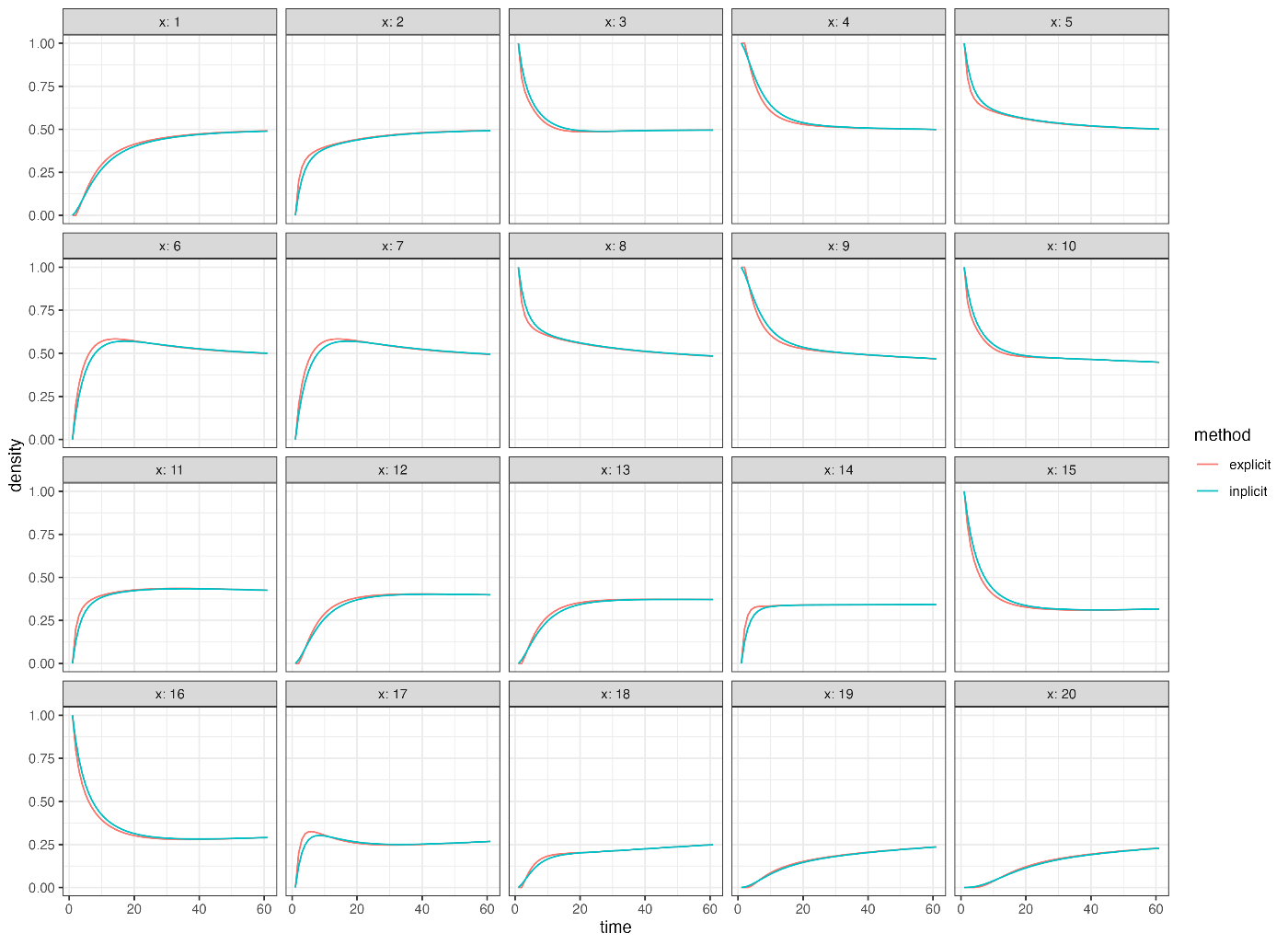
次に, 拡散係数 a=0.5 として陽解法による結果:
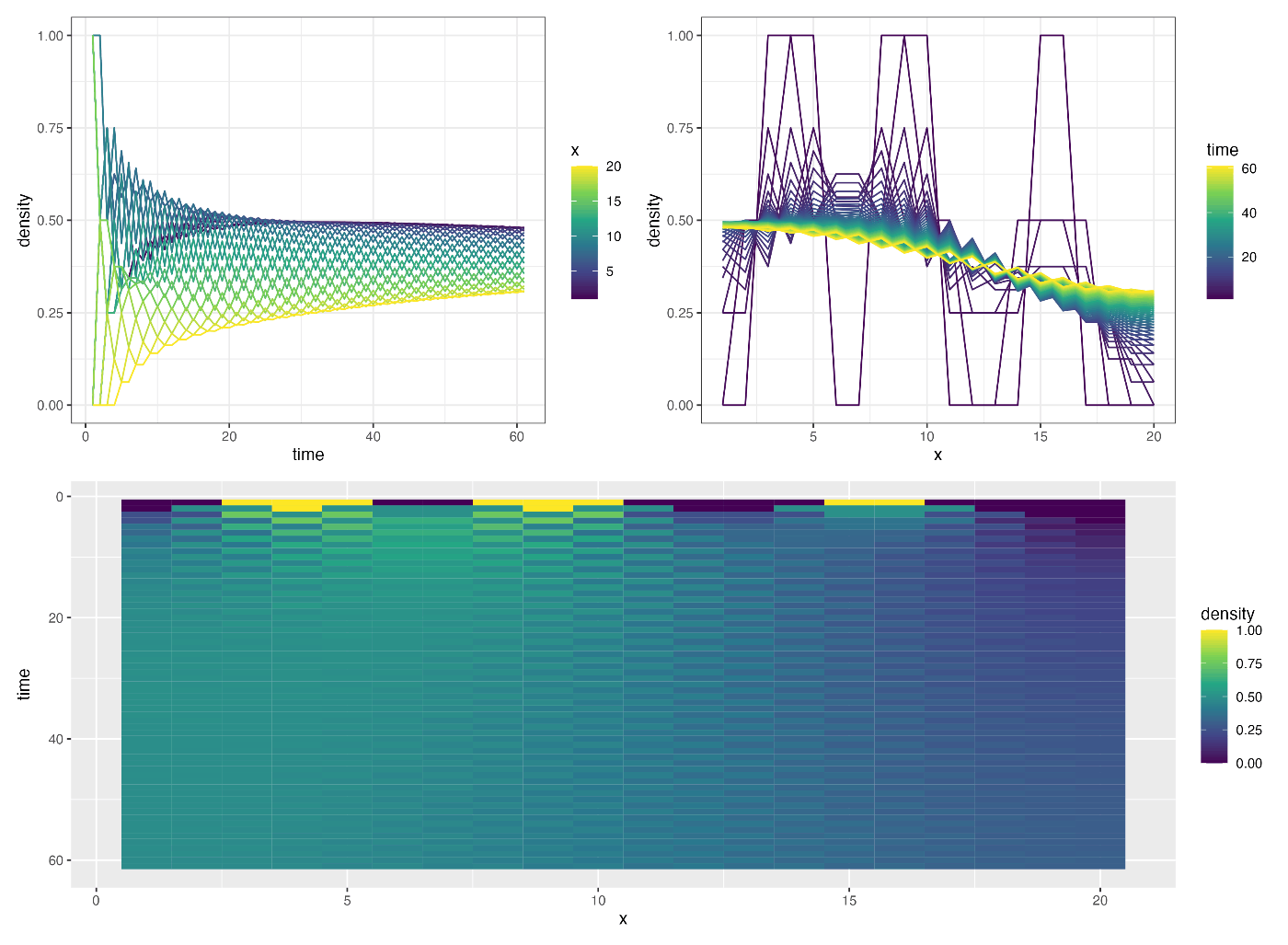
濃度が上がったり下がったりしていて拡散のシミュレーションとしては不適当である.
拡散係数 a=0.5 として陰解法による結果:
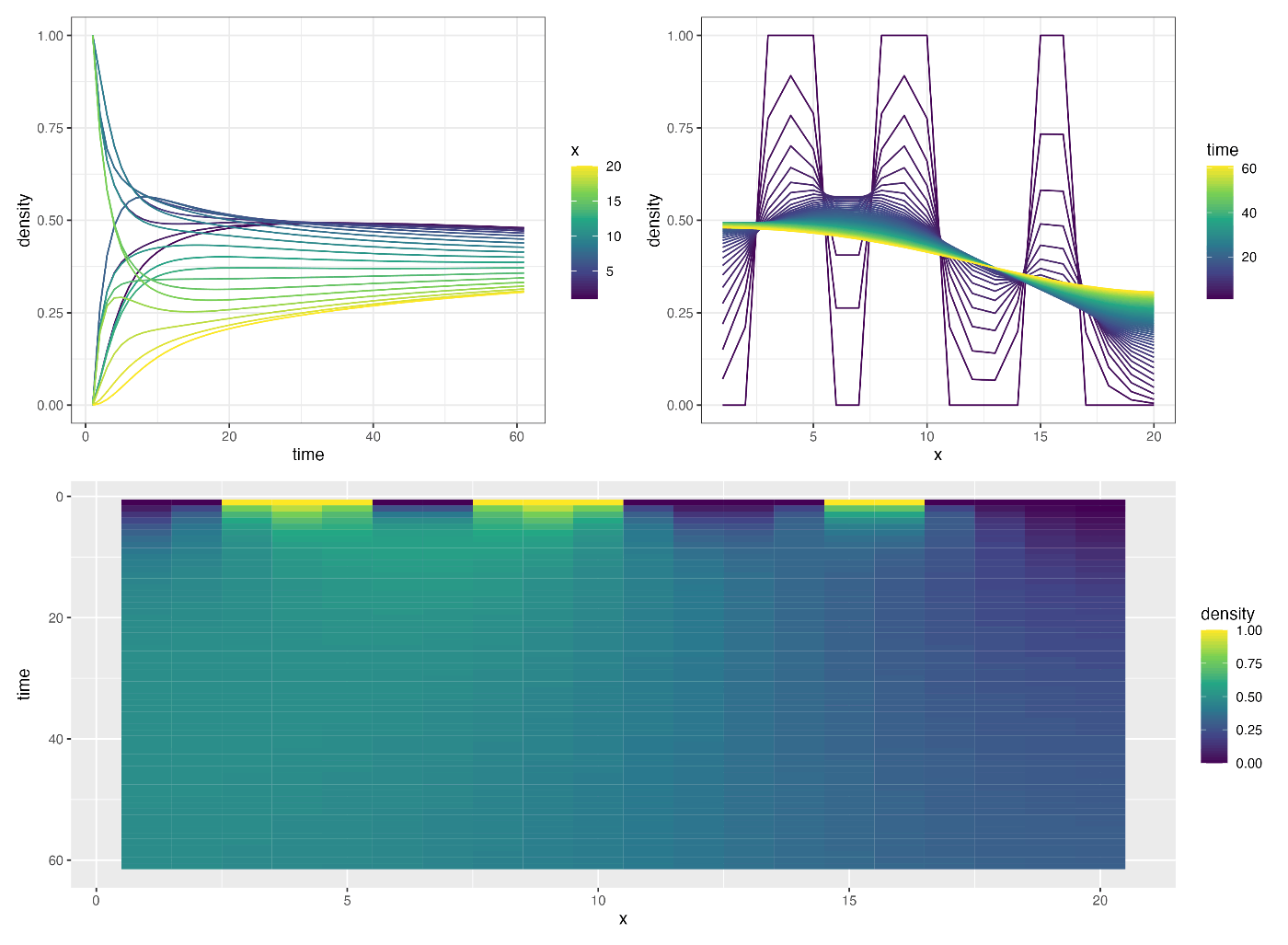
こちらはうまくいってそう.
陰解法のほうが安定して計算できそうなので以降は陰解法を使うことにする.
たぶんこれらの解法が使える条件とか解の精度について, 本当はある程度解析的に求められるんじゃないかと思う. が, よく知らないのでこれ読むといいよーみたいなのがあったら教えてください.
状態空間モデル
状態空間モデルとは次のような確率分布の組で表されるモデルのことを指す:
\begin{aligned}
y_t &\sim f(y_t|x_t) \\
x_t &\sim f(x_t|x_{t-1}).
\end{aligned}
今回はなかでも次の形で書ける正規線形の状態空間モデルについて考える:
\begin{aligned}
y_t &= Fx_t + \varepsilon_t, \quad \varepsilon_t \sim \mathcal{N}(\varepsilon_t|0, V)\\
x_t &= Gx_{t-1} + \eta_t, \quad \eta_t \sim \mathcal{N}(\eta_t|0, W).
\end{aligned}
\varepsilon_t \sim \mathcal{N}(\varepsilon_t \sim |0, V) は「確率変数\varepsilon_t が平均0, 分散Vの正規分布に従う」を意味する.
x_t = Gx_{t-1} + \eta_t を x_t \approx Gx_{t-1} のように書き直してみると, (1'')や(2'')との類似がわかりやすくなるのではないかと思う.
Rによる計算例(ノイズあり)
状態 x_t についてはカルマンフィルタで推定し, 固定パラメータ(分散と拡散係数)については最尤法で求めることにする. dlmパッケージを使う.
カルマンフィルタ自体については別の文献を参照してほしいが, 何を読むのがいいんだろう.
とりあえず
野村俊一『カルマンフィルタ―Rを使った時系列予測と状態空間モデル―』(共立出版)
のアマゾンアフィリエイトリンクを貼っておきます(ただしこの本はdlmパッケージは使ってない).
離散化した拡散方程式に正規乱数で少しノイズを乗せてシミュレーションしてみる:
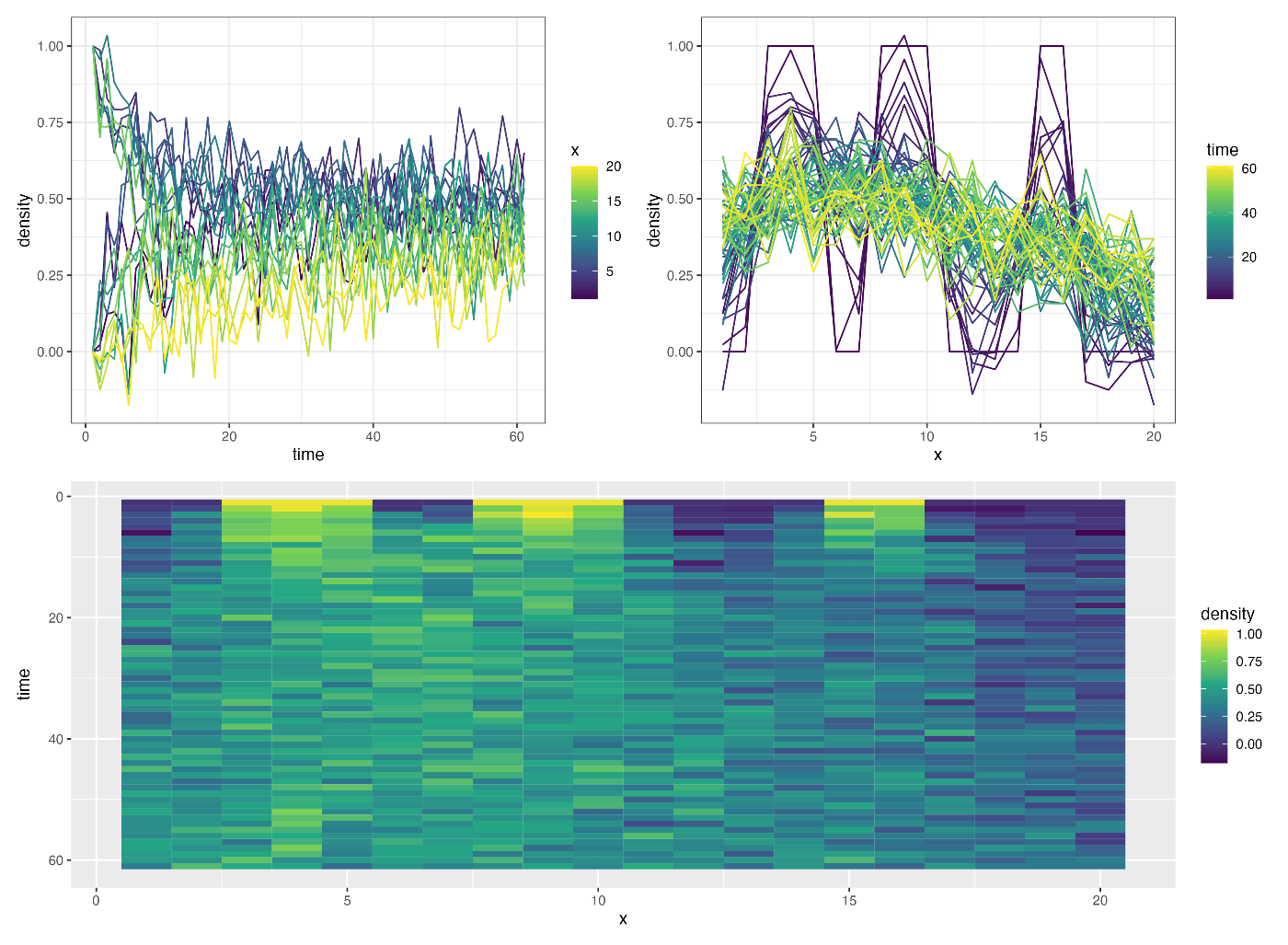
カルマンフィルタとスムーザーによるフィッテングの確認:
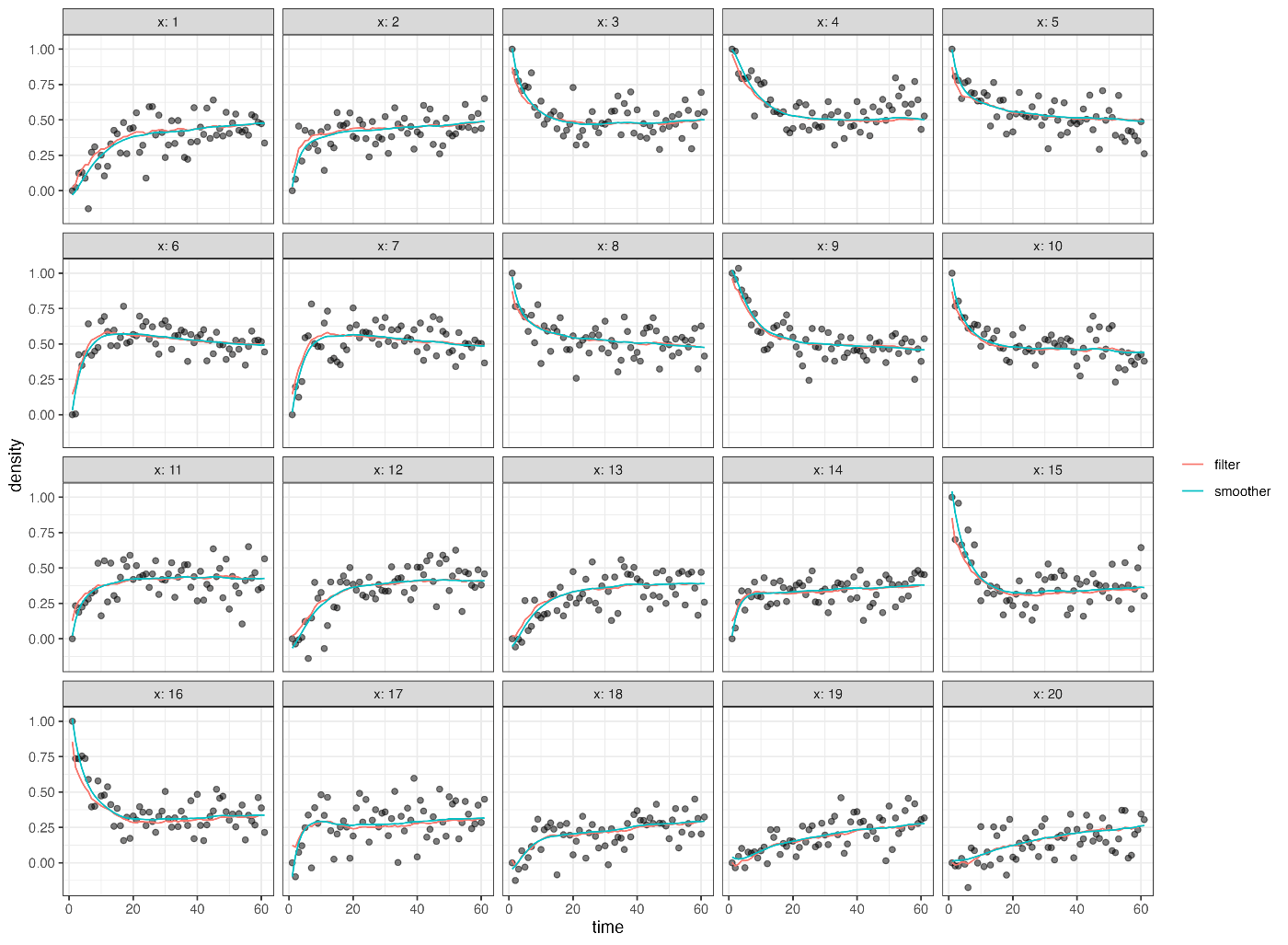
スムージングの結果:
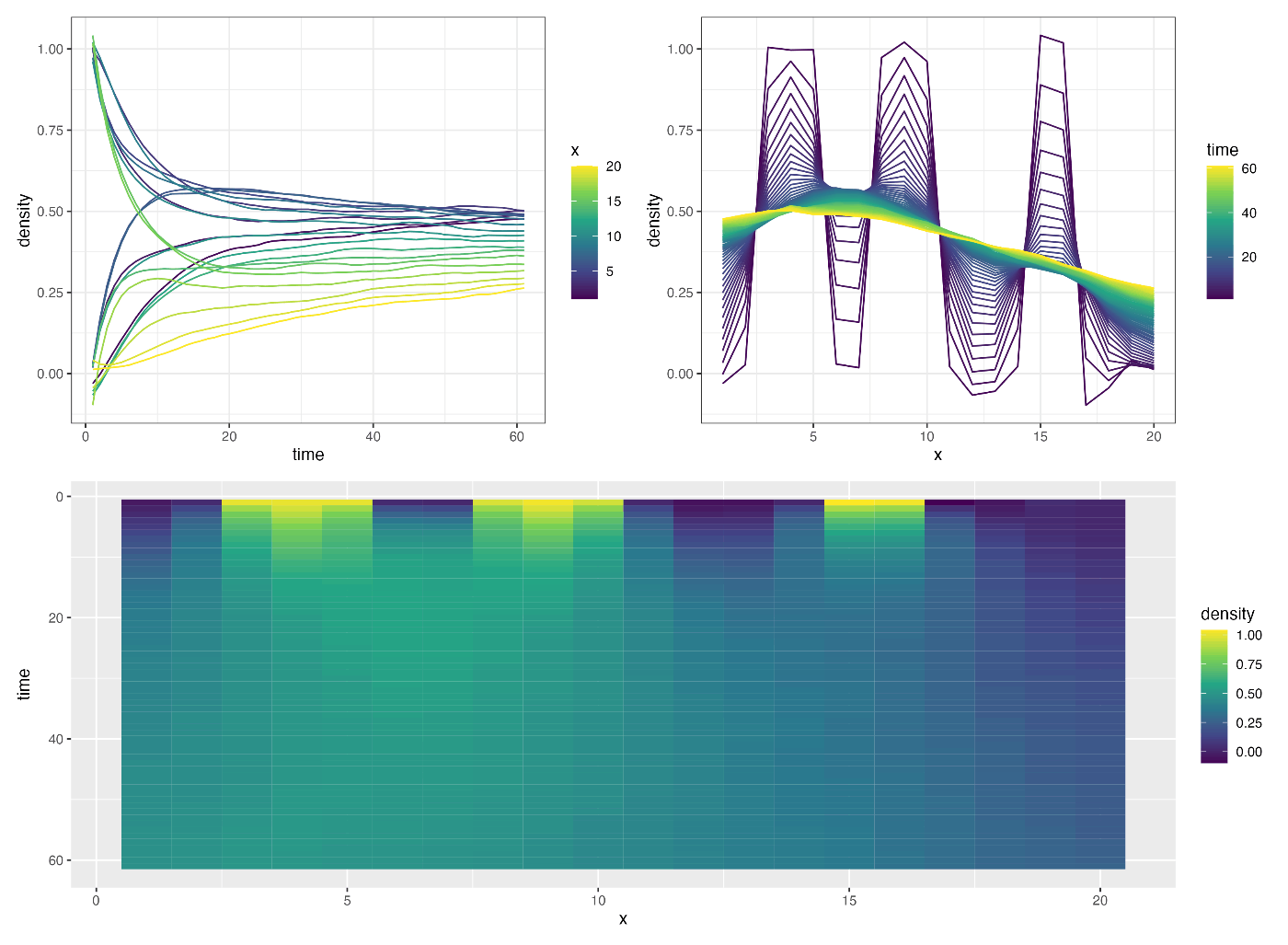
使用したコードはすべてまとめて以下に公開する:








Discussion