◾

GLSLで7つのボーダー繰り返しパターン

2024/10/27に公開

glsl

tech

一直線上に展開するボーダーの繰り返しパターンは7つのタイプに分類することができるといわれています。この記事ではGLSLを用いてシェーダーで7つのボーダー繰り返しパターンの実装を試してみます。

7つのボーダー繰り返しパターン

1 (並進)

モチーフが一方向に並進するだけの繰り返しパターンです。

vec2 borderPattern1(vec2 p, float aspect) {
    vec2 q = vec2(mod(p.x, aspect), p.y);
    return q;
}

ボーダーはX方向に展開し、引数pのy要素は[0, 1]の範囲にあると想定しています。引数aspectで指定した値により、モチーフのアスペクト比がaspect:1になります。以下の例では1.0を指定しているので1:1になります。これらの引数は他の繰り返しパターンでも同様です。

vec2 p = v_texcoord * resolution / resolution.y;
vec2 q = borderPattern1(p, 1.0);
gl_FragColor = vec4(q, 0.0, 1.0);

モチーフとして三角形を描画すると以下のようになります。drawTriangle関数の詳細な実装はこの記事の最後に補足として載せています。

float v = drawTriangle(q);
gl_FragColor = vec4(vec3(v), 1.0);

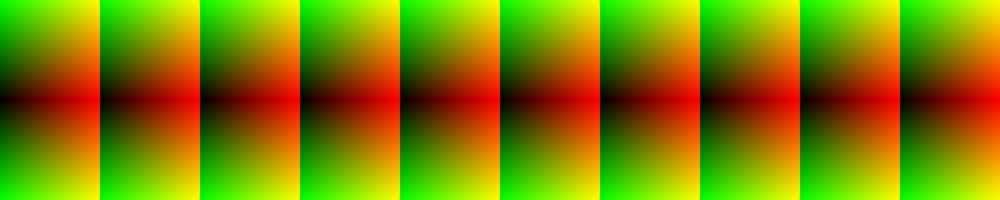
1m (移動方向を軸に鏡映)

モチーフが移動方向を軸に鏡映して展開する繰り返しパターンです。

vec2 borderPattern1m(vec2 p, float aspect) {
    vec2 q = vec2(mod(p.x, aspect * 0.5) * 2.0, abs(p.y - 0.5) * 2.0);
    return q;
}

使用例は以下のようになりますが、関数呼び出し以外はパターン1と同様なので省略しています。

vec2 q = borderPattern1m(p, 1.0);

g (すべり鏡映)

モチーフが移動方向を軸にすべり鏡映して展開する繰り返しパターンです。

vec2 borderPatternG(vec2 p, float aspect, float glind) {
    float a = 0.5 * aspect;
    vec2 q = vec2(mod(p.x - step(p.y, 0.5) * glind * a, a) * 2.0, abs(p.y - 0.5) * 2.0);
    return q;
}

引数glindには鏡映後の移動量を[0, 1]で指定します。

vec2 q = borderPatternG(p, 1.0, 0.5);

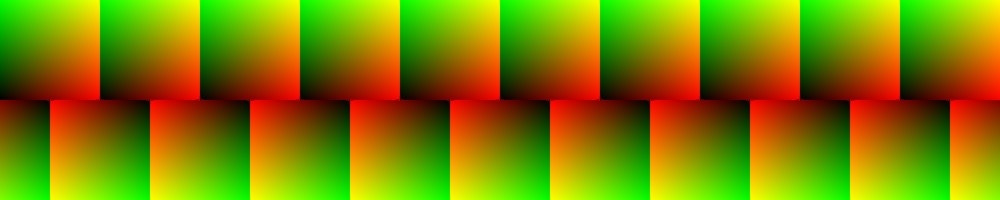
2 (2回割の回転)

モチーフが2回割(180度)回転して展開する繰り返しパターンです。


vec2 borderPattern2(vec2 p, float aspect, float center) { 
    float a = 0.5 * aspect;
    vec2 q = vec2(mod(p.x - step(p.y, 0.5) * center * a, a) * 2.0, abs(p.y - 0.5) * 2.0);
    q.x = p.y > 0.5 ?  q.x : aspect - q.x;
    return q;
}

引数centerには回転中心の位置を[0, 1]で指定します。

vec2 q = borderPattern2(p, 1.0, 0.5);

m1 (移動方向に直交する軸で鏡映)

モチーフが移動方向に直交する軸で鏡映して展開する繰り返しパターンです。

vec2 borderPatternM1(vec2 p, float aspect) {
    vec2 q = vec2(mod(p.x, aspect), p.y);
    q.x = mod(p.x, 2.0 * aspect) < aspect ? q.x : aspect - q.x;
    return q;
}

vec2 q = borderPatternM1(p, 1.0);

mm (二方向の鏡映)

モチーフが移動方向の軸で鏡映して、さらに移動方向を直交する軸で鏡映して展開する繰り返しパターンです。

vec2 borderPatternMm(vec2 p, float aspect) {
    float a = 0.5 * aspect;
    vec2 q = vec2(mod(p.x, a) * 2.0, abs(p.y - 0.5) * 2.0);
    q.x = mod(p.x, aspect) < a ? q.x : aspect - q.x;
    return q;
}

vec2 q = borderPatternMm(p, 1.0);

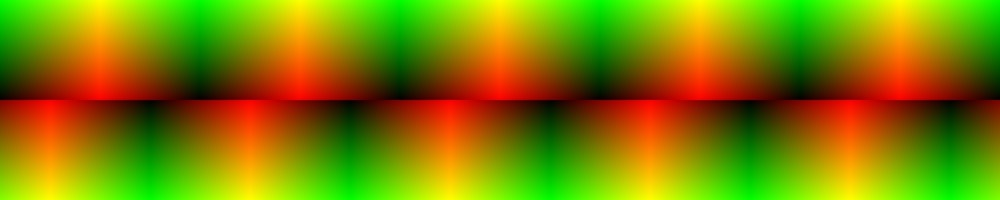
mg (鏡映 + すべり鏡映)

モチーフが移動方向に直交する軸で鏡映して、さらに移動方向の軸ですべり鏡映して展開する繰り返しパターンです。

vec2 borderPatternMg(vec2 p, float aspect, float glind) {
    float a = 0.5 * aspect;
    float px = p.x + step(p.y, 0.5) * a * glind;
    vec2 q = vec2(mod(px, a) * 2.0, abs(p.y - 0.5) * 2.0);
    q.x = mod(px, aspect) < a ? q.x : aspect - q.x;
    return q;
}

パターンgのときと同様に引数glindには鏡映後の移動量を[0, 1]で指定します。

vec2 q = borderPatternMg(p, 1.0, 0.5);

補足

三角形の描画

#define PI 3.14159265359

// https://iquilezles.org/articles/distfunctions2d/
float sdTriangleIsosceles( in vec2 p, in vec2 q )
{
    p.x = abs(p.x);
    vec2 a = p - q*clamp( dot(p,q)/dot(q,q), 0.0, 1.0 );
    vec2 b = p - q*vec2( clamp( p.x/q.x, 0.0, 1.0 ), 1.0 );
    float s = -sign( q.y );
    vec2 d = min( vec2( dot(a,a), s*(p.x*q.y-p.y*q.x) ),
                  vec2( dot(b,b), s*(p.y-q.y)  ));
    return -sqrt(d.x)*sign(d.y);
}

mat2 rotate(float r) {
    float c = cos(r);
    float s = sin(r);
    return mat2(c, s, -s, c);
}

float drawTriangle(vec2 p) {
    float d = sdTriangleIsosceles(rotate(-PI / 4) * (p * 2.0 - 1.0) - vec2(0.0, - 0.8), vec2(0.5, 1.2));
    return step(0.0, d);   
}

参考

装飾パターンの法則