[論文紹介] AdaLoRA

ICLR22のLoRA^[1]の後続研究であるAdaLoRA^[2]（ICLR23にposterで採択）の解説です．

書誌情報です．
Q. Zhang, M. Chen, A. Bukharin, P. He, Y. Cheng, W. Chen, and T. Zhao, "Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning," in ICLR, 2023.

輪講スライドも公開してるので，良ければそちらも参照していただければ．
https://speakerdeck.com/keio_smilab/journal-club-adaptive-budget-allocation-for-parameter-efficient-fine-tuning

関連リンク

• ガチプロによる査読であるところのOpen Review
• Paper
  • ICLR23版
  • arXiv版
• PEFT v0.3.0における実装箇所
  • src/peft/tuners/adalora.py - class AdaLoraModel
  • src/peft/tuners/adalora.py - class AdaLoraLayer
  • src/peft/tuners/adalora.py - class SVDLinear
  • src/peft/tuners/adalora.py - class RankAllocator
  • （本家実装はリンク切れ：https://github.com/QingruZhang/AdaLoRA）

SUMMARY

LoRAの派生手法であるAdaLoRAを提案

• 増分行列 $\Delta$ に対して特異値分解に基づいた分解を行う ($\Delta = P \Lambda Q$)
• LoRAでは固定だったランク $r$ の値をLoRAを適用する層に応じて 適応的に変化 させる ( $\Lambda$ のサイズを変化させる)
• LoRAなどのベースライン手法を上回るパフォーマンス
• 定性的結果で研究の動機を回収

前提：LoRA

深層学習モデルのfine-tuningにおいて，全てのパラメータを更新する代わりにパラメータの増分のみを最適化することを考えます．
例えばあるLLMが持つある線形層のパラメータ行列 $W^{(0)} \in \mathbb{R}^{d_1 \times d_2}$ をfine-tuningして得られるパラメータ行列 $W$ は $W^{(0)}$ に対する増分行列 $\Delta$ を用いて $W = W^{(0)} + \Delta$ と表せます．
(増分行列：fine-tuningによるパラメータの変化量．c.f., "accumulated gradient update during adaptation")

その際，LoRAではこの増分行列 $\Delta \in \mathbb{R}^{d_1 \times d_2}$ を行列 $B \in \mathbb{R}^{d_1 \times r}, A \in \mathbb{R}^{r \times d_2}$ を用いて $\Delta = BA$ と近似します．
すると学習可能パラメータの数は $d_1d_2$ から $(d_1 + d_2)r$ に削減できます． $r << \min(d_1,d_2)$ である場合に大きく学習可能パラメータ数を削減できることが分かるかと思います．

LoRA: eye-catch figure + note

LoRAの嬉しい所をざっくり3つ挙げます．

• 元のモデルにアダプタネットワークとして $\Delta = BA$ をくっつけて走らせることになるので，そもそも元のモデルのforward passの計算がメモリに載らない場合は厳しいですが，backward passの計算のために勾配をメモリに載せておく必要があるパラメータの数を大きく削減できるのが嬉しいです．
• また，増分行列 $\Delta$ (= 学習によるパラメータの差分)を求めているので，推論時はLoRAのアダプタで求めた増分行列を直接元のモデルに足してアダプタを外せば，アダプタによる推論時のオーバーヘッドはなくなります．
• さらに，複数のタスクに向けて個別にfine-tuningしたモデルを用意したいとき，モデル全体をfine-tuningする場合は事前学習済みモデルと同様の大きさのモデルを複数保管する必要がありましたが，LoRAであればタスクごとに求めた増分行列のみを保持すればよいので，より少ないパラメータを保持しておけば良く，省スペースです．

このLoRAについてはもうだいぶ知っている人が多いと思います．ICLR22の元論文はLLMのパラメータ全てを更新するのはexpensiveなのでもっと効率的にモデルを調整したいというモチベーションからLoRAを提案していますが，条件付き画像生成モデルであるStable DiffusionやControlNetのfine-tuningにおいてもLoRAが利用されるようになっています．
良い資料もあるので，興味がある方は参照してください．

モチベーション：LoRAの問題点

LoRAは各増分行列 $\Delta$ のランク $r$ を事前に一つに固定しているという制約があります．これはfine-tuningを行う際に，層やモジュールによってパラメータの重要度が異なるという事実を無視しています．

以下はある層，あるモジュールのみにLoRAを適用した際のMNLI-mのパフォーマンスの差を示す図です(縦軸注意です)．

(a) Apply LoRA to selected weight matrix

(b) Apply LoRA to selected layers

まぁ数回実験したらひっくり返りそうな程度の差ですが，例えば図(b)の1-3層に適用した場合と10-12層に適用した場合を見るとこれはたしかに差はありそうです．

提案：AdaLoRA

AdaLoRAはLoRAでは固定だったランク $r$ の値をLoRAを適用する層に応じて適応的に変化させる派生手法です．新規性は大きく分けて2つ，(i) 特異値分解に基づく適応，(ii) 重要度によるランクの割り当てとなります．

(i) 特異値分解に基づく適応

増分行列の分解

さて，LoRAは深層学習モデルのあるパラメータ行列 $W$ の増分行列 $\Delta \in \mathbb{R}^{d_1 \times d_2}$ を2つの低ランク行列 $B \in \mathbb{R}^{d_1 \times r}, A \in \mathbb{R}^{r \times d_2}$ の行列積に分解する手法でした(低ランク近似)．

$$W = W^{(0)} + \Delta = W^{(0)} + BA$$

これに対してAdaLoRAは次のように増分行列 $\Delta$ を分解します．

$$W = W^{(0)} + \Delta = W^{(0)} + P \Lambda Q$$

ここで $P \in \mathbb{R}^{d_1 \times r}$ ， $\Lambda \in \mathbb{R}^{r \times r}$ ，そして $Q \in \mathbb{R}^{r \times d_2}$ です．

この式で一番見て欲しいところは勿論末尾の $P \Lambda Q$ ですが，これは 特異値分解のオマージュ です．即ち， $P$ 及び $Q$ は左右の特異ベクトルを $r$ 個並べた直交行列， $\Lambda$ は $r$ 個の対応する特異値を対角成分に持つ対角行列になることが期待されます．ただしこれらはアルゴリズミックに計算されるわけではなく，学習可能パラメータとしてback prop.で最適化されます(その意味で特異値分解のオマージュと言いました)．

ただ，これだけでは $P \Lambda Q$ が特異値分解の形をとることが保証されないので， $P, Q$ それぞれが直交性を持つように以下の正則化を行います．

$$R(P, Q) = \Vert P^T P - I \Vert_\mathrm{F}^2 + \Vert Q Q^T - I \Vert_\mathrm{F}^2$$

この正則化項を係数 $\gamma$ で重み付けして損失に加えておけば良いです．
(特異値を $\Lambda$ に押し付けているので特異値分解ができていれば $P^T P$ や $Q Q^T$ は対角行列ではなく単位行列になります)

また，$P \Lambda Q$ の初期値を $0$ にするため，$P$ ， $Q$ はそれぞれガウシアンノイズで初期化され， $\Lambda$ はゼロで初期化されます．

アルゴリズミックに特異値分解をして特異値の大きさを元に適応的に $r$ の値を変化させることもできるのではという疑問があるかもしれませんが，著者らは計算コストの観点からback prop.に基づく $P \Lambda Q$ の最適化を採用しています．ある行列 $M \in \mathbb{R}^{d_1 \times d_2}$の特異値分解の計算量は $O(\min(d_1, d_2) d_1 d_2)$ に従うと著者らは指摘しています．

特異値ごとに分解した定式化

後の議論のために， $P \Lambda Q$ の分解を特異値ごとに書いた定式化をしておきます．
$\Lambda$は対角行列 $\mathrm{diag}(\lambda_1, \lambda_2, \dots, \lambda_r)$ なので，対角成分だけを見ればよいです．そのため，以下の三つ組(triplet)を定義します．

$$\mathcal{G}_i = \left\{ P_{*i}, \lambda_i, Q_{i*} \right\} \; (i = 1, \dots, r)$$

さらに，ネットワーク内の全てのパラメータ行列の内，AdaLoRAを適用するパラメータ行列が $n$ 個あることにします．その時 $k$個目の増分行列を $\Delta_{k}$ とし，そして$k$個目の増分行列の特異値ごとのtripletは次のように書きます．

$$\mathcal{G}_{k, i} = \left\{ P_{k, *i}, \lambda_{k, i}, Q_{k, i*} \right\} \; (i = 1, \dots, r;\: k = 1, \dots, n)$$

(ii) 重要度によるランクの割り当て

特異値 $\lambda_{k,i}$ の更新

半分終わりました！ここからはランク $r$ を適応的に変化させる部分についてみていきます．

ランクを適応的に変化させるために，まずは各triplet $\mathcal{G}_{k,i}$ の重要度 $S_{k, i}^{(t)}$ を定義します．重要度は学習段階によって変化するので，学習ステップ $t$ を右肩に添えています．

次はこの重要度 $S_{k,i}$ をもとに各特異値 $\lambda_{k,i}$ をON/OFFすることでランク $r$ を操作する方法を考えます．
結論から言うと次の式で更新を行います．

$$\lambda_{k,i}^{(t+1)} \leftarrow \left\{\begin{matrix} \quad \tilde{\lambda}_{k,i}^{(t)} &\qquad\mathrm{if}\: S_{k,i}^{(t)} \;\mathrm{is} \:\mathrm{in} \:\mathrm{the} \:\mathrm{top-}b^{(t)} \:\mathrm{of} \:\mathrm{every} \: S^{(t)}, \\\\ \quad 0 &\qquad\mathrm{otherwise} \end{matrix}\right.$$

ここで $\tilde{\lambda}_{k,i}^{(t)}$ は学習ステップ $t$ における特異値パラメータ $\lambda_{k,i}^{(t)}$ のback prop.による更新後の値です．

つまり，重要度の高い順に $b^{(t)}$ 個のパラメータのみ残して他は0にする操作を毎ステップ行っています．

Triplet $\mathcal{G}_{k,i}$ の重要度 $S_{k,i}$ の定義

$\mathcal{G}_{k,i}$ の重要度 $S_{k,i}$ として $\lambda_{k,i}$ だけでなく 特異ベクトル $P_{k, *i}$， $Q_{k, i*}$ の値も考慮した重要度を定義します．

$$S_{k,i} = s(\lambda_{k,i}) + \frac{1}{d_1} \sum_{j=1}^{d_1} s(P_{k,ji}) + \frac{1}{d_2} \sum_{j=1}^{d_2} s(P_{k,ij})$$

第2，3項ではパラメータサイズに左右されないように， $P_{k, *i}$ と $Q_{k, i*}$ それぞれの平均を取っています．

ここで $s(\cdot)$ が出てきました．これは重要度の計算に用いる関数で，著者らはZhang et al. (2022)^[3]に従って $\bar{I}^{(t)}(w_{ij})$， $\bar{U}^{(t)}(w_{ij})$ を定め，次のように定義しています．

$$\begin{matrix} I(w_{ij}) &=& \left\vert w_{ij} \nabla_{w_{ij}} \mathcal{L} \right\vert \\\\ \bar{I}^{(t)}(w_{ij}) &=& \beta_1 \bar{I}^{(t-1)} (w_{ij}) + (1 - \beta_1) I^{(t)} (w_{ij})\\\\ \bar{U}^{(t)}(w_{ij}) &=& \beta_2 \bar{U}^{(t-1)} (w_{ij}) + (1 - \beta_2) \left\vert I^{(t)} (w_{ij}) - \bar{I}^{(t)} (w_{ij}) \right\vert \\\\\\ s^{(t)}(w_{ij}) &=& \bar{I}^{(t)}(w_{ij}) \cdot \bar{U}^{(t)}(w_{ij}) \end{matrix}$$

ここで $w_{ij}$ は $s(\cdot)$ 対象とする学習可能パラメータです．

簡単におきもちだけ説明します．
$I(w_{ij})$ はそのパラメータを0にした時の損失 $\mathcal{L}$ の変化量を推定するために導入されたsensitivityです．Zhangらは確率的にミニバッチがサンプリングされること，複雑な学習ダイナミクスが原因でこのsensitivityの推定は不安定になると主張し，指数移動平均を利用したsmoothed sensitivity $\bar{I}^{(t)}(w_{ij})$ と不確実性項 $\bar{U}^{(t)}(w_{ij})$ を導入し，それらの積で当該パラメータの重要度を定義しています．

バジェット $b^{(t)}$ のスケジューリング

最後です．学習を円滑に進めるため，バジェット $b^{(t)}$ のスケジューリングを導入します．
具体的には $b^{(t)}$ の初期値 $b^{(0)}$ と目標値 $b^{(T)}$ を定め，次のようにスケジューリングします．

$$b^{(t)} = \left\{\begin{matrix} \:b^{(0)} & \quad 0 \leq t < t_i \\\\ \:b^{(T)} + (b^{(0)} - b^{(T)}) \left( 1 - \frac{t-t_i-t_f}{T-t_i-t_f} \right)^3 & \quad t_i \leq t < T - t_f \\\\ \:b^{(t)} & \quad \mathrm{otherwise} \end{matrix}\right.$$

雰囲気が分かりやすいかもしれないので，一例を図にしましたどうぞ

実験結果

定量的結果

2つだけ紹介します．
以下の表はDeBERTaV3-baseに対してAdaLoRAやベースライン手法を使って学習を行った際のGLUE development setにおける結果です．
この結果はseedを変えて行った5回の実験の平均値であり，p < 0.05と報告されています．

Results with DeBERTaV3-base on GLUE development set.
大体AdaLoRAが勝っていそうです．

もう一つは学習可能パラメータ数を変化させてLoRAとAdaLoRAのパフォーマンスを比較するものです↓(例によって縦軸注意です)．

left: MNLI, middle: SQuADv2.0, right: XSum

一貫してAdaLoRAの方が良いパフォーマンスです．

定性的結果

モチベーションの回収を行っているので個人的おもしろポイントです．
以下の図はDeBERTaV3-baseをAdaLoRAによってMNLIでfine-tuningした結果，モジュール，層ごとのランク $r$ の値を可視化したものです．

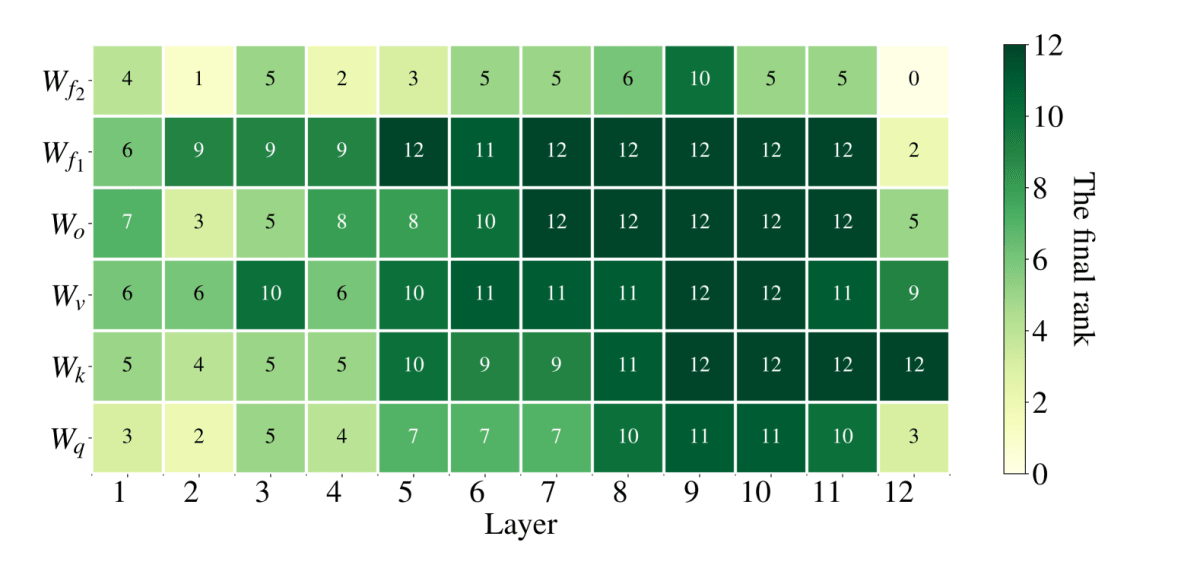
Rank of each incremental matrix when fine-tuning DeBERTaV3-base on MNLI with AdaLoRA

この図を見る限り，大まかに深い層に割り当てられるランクが偏っており，また線形層のパラメータ $W_{f_1}$ に多く割り当てられています．

ここでモチベーションに戻りますが，

fine-tuningを行う際に，層やモジュールによってパラメータの重要度が異なる

と主張し，実際に特定の層，モジュールのみにLoRAを適用した際のMNLI-mのパフォーマンスの差を示す図

(a) Apply LoRA to selected weight matrix

(b) Apply LoRA to selected layers

を見るとより深い層をtuningした方がパフォーマンスが良く，同様に線形層のパラメータをtuningした方がパフォーマンスが良いことが分かります．

→完全にとは言いませんが，最初の検証実験の結果にある程度沿った定性的結果が得られています．

SUMMARY

LoRAの派生手法であるAdaLoRAを提案

• 増分行列 $\Delta$ に対して特異値分解に基づいた分解を行う ($\Delta = P \Lambda Q$)
• LoRAでは固定だったランク $r$ の値をLoRAを適用する層に応じて 適応的に変化 させる ( $\Lambda$ のサイズを変化させる)
• LoRAなどのベースライン手法を上回るパフォーマンス
• 定性的結果で研究の動機を回収

p.s. 既にHuggingFace PEFTに実装されていて動かせるので試してみてはいかがでしょう．例えばAlpaca-LoRAはPEFTを使っていますから，configを軽く書き換えるだけで試せます．

脚注

1. E. J. Hu, yelong shen, P. Wallis, Z. Allen-Zhu, Y. Li, S. Wang, L. Wang, and W. Chen, "LoRA: Low-Rank Adaptation of Large Language Models," in ICLR, 2022

2. Q. Zhang, M. Chen, A. Bukharin, P. He, Y. Cheng, W. Chen, and T. Zhao, "Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning," in ICLR, 2023.

3. Q. Zhang, S. Zuo, C. Liang, A. Bukharin, P. He, W. Chen, and T. Zhao, "Platon: Pruning large transformer models with upper confidence bound of weight importance," in ICML, 2022, pp. 26809–26823.