HaskellからPythonに翻訳して何かを味わう

概要

私が書いた別グループの記事から見たほうがわかりやすいです。以下のこの記事は日本語が残念、、、いつか修正したい。

このPDF資料において、プロトタイプを作る上でのHaskellの優位性が書かれています。
具体的なコードの全体が示されていないので実際に書いてみました。また上記資料にはPythonについて検証されていないので、Pythonバージョンのコードも書いてみて比較考察してみました。その際はラムダ式を使うようにしています。

私はもともとC/C++やPythonをメインに使っていました。見識を広げるためにHaskellを勉強していまして、それがどれほど手続き型言語(の関数型的書き方)に応用できるのか知りたく思っていました。

課題

以下図は上記で示したPDF資料から取っています。
軍事系の課題でして、防衛機能を持つ船(Aegis Ship)や運搬用の船(Carrier)の定義範囲に敵の飛行機(Hostile Aircraft)が在るか否かを2Dの幾何学情報から判断します。

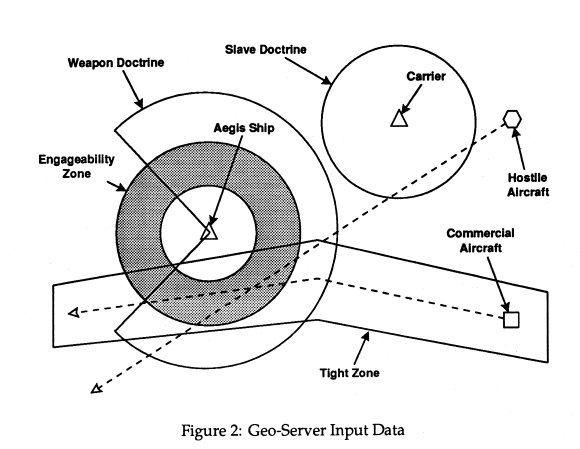
定義範囲は戦闘(接触?)範囲(Engageability Zone)のような中空の円だったり只の円や扇形だったりします。また、このページでは扱いませんが民間飛行機の航路や海岸線などの多角形もあります。

円(Slave Doctrine)

上記資料に倣い、円内に任意の点が在るか判定するラムダ式を返す関数circleを書きました。
関数型言語らしいですね。なお、引数pは相対座標です。

type Radius = Float
type Radian = Float
type Point = (Float, Float)
type Region = Point -> Bool

inRegion :: Point -> Region -> Bool
p `inRegion` r = r p

distance :: Point -> Float
distance (x, y) = sqrt $ x ^2 + y^2

diff2D :: Point -> Point -> Point
diff2D (x1, y1) (x2, y2) = (x1 - x2, y1 - y2)

circle  :: Radius -> Region
circle r = \p -> r > distance p

以下のように使えます。

let c1 = circle 50
let rel_pos = diff2D (x,y) (50.0, 50.0)
let result = rel_pos `inRegion` c1

Pythonは以下です。

Point = Tuple[float, float]
Region = Callable[[Point], bool]

def in_region(p: Point, r: Region) -> bool:
    return r(p)

def distance(p: Point) -> float:
    x, y = p
    return math.sqrt(x ** 2 + y ** 2)

def diff2D(p1: Point, p2: Point) -> Point:
    x1, y1 = p1
    x2, y2 = p2
    return x1 - x2, y1 - y2

def circle(r: float) -> Region:
    return lambda p: r > distance(p)

HaskellとPythonでほぼ違いは無いですね。ただdistanceで引数を読み出す時に、Haskellはx,yに直接引数を展開できていますがPythonではx,y=pを一行書く必要がありました。ここはHaskellの好きなところです。

私はcircleの様にラムダ式を返す関数を書いたことが無くて、ラムダ式はPythonでもせいぜいmapやfilterに引数として渡す際に使う程度でした。なのでラムダ式を返す関数を作ることで何が嬉しいのかはまだ実感が持てていませんでした。以下のように書けば済むからです。

def in_circle_monolis(p_target: Point, r: Radius) -> bool:
    d = distance(p_target)
    return (d < r)

なにか有利に働くような気がする局面は次の章に書きます。

ランダム生成した点群を処理させた結果は以下です。

let c1 = circle 50
let rel_pos = diff2D (x,y) (50.0, 50.0)
let result = rel_pos `inRegion` c1

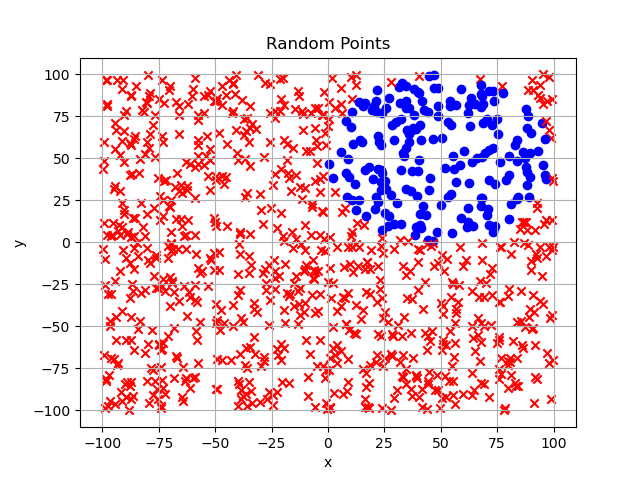
中空円(Engageability Zone)

課題で示した網がけの領域のように、船を取り囲む中空円に敵が在るかを判断します。
中空なので敵が接近しすぎると判定しません。それは上記PDF資料が意図したことでしょうが、
なぜ中空円なのかまでは読めていません。砲台の仰角制限などが関係しているのかな？おそらく迎撃可能な範囲を示すためでしょう。
annulus関数が中空円内判定用の関数です。circleと同様にその判定を行うラムダ式Regionを返します。
Haskell:

outside :: Region -> Region
outside re = \p -> not $ re p

(/\)    :: Region -> Region -> Region
r1 /\ r2 = \p -> r1 p && r2 p

annulus :: Radius -> Radius -> Region
annulus r1 r2 = (outside (circle r1)) /\ (circle r2)

Python:

def outside(r: Region) -> Region:
    return lambda p: not r(p)

def and_region(r1: Region, r2: Region) -> Region:
    return lambda p: r1(p) and r2(p)

def annulus(r1: float, r2: float) -> Region:
    return lambda p: outside(circle(r1))(p) and circle(r2)(p)

HaskellではRegionのAndとして演算子/\を定義しています。Pythonでも演算子オーバーロードでできますが、行が長くなるのでやめておきました。Haskellは簡単に書けてますね。

前章のcircle関数を、ラムダ式Regionを返す関数にすることでRegion同士の演算でannulus関数が表現出来ています。これは感動がありますが前章のin_circle_monolis同様、やはり以下のように書いたほうが書く際には簡単ですよね？outsideもand_regionも不要に感じます。

def in_annulus_monolis(p_target: Point, r1: Radius, r2: Radius) -> bool:
    d = distance(p_target)  
    return (d > r1) and (d < r2)

書いて1年経って見た時にどうでしょうか。そのときにはannulusという単語の意味を忘れているわけです。その時にoutside(circle(r1))(p) and circle(r2)(p)はannulusの本質を良く伝えるでしょう。in_annulus_monolisのコードから中空円が定義されていることは察するのに時間がかかります。このドキュメント性は元資料でもHaskellの良い性質として言及されていますが、しかし単に関数型を使っていても意識的に書かなければ得られる性質では無いですね、、、

outsideや、and_region(/\)などのRegionの幾何学的演算を抽象的に表現したことは、再利用性の面でも利点がありそうですが、抽象化が過ぎている気もします。どれだけ複雑な領域演算を行うかに拠るのでしょうが、そもそも関数設計計画が立っていないプロトタイプであるならば書いておいて損は無さそうです。

点群処理の結果は以下です。

let a1 = annulus 20 50
let rel_pos = diff2D (x,y) (50.0, 50.0)
let result = rel_pos `inRegion` a1

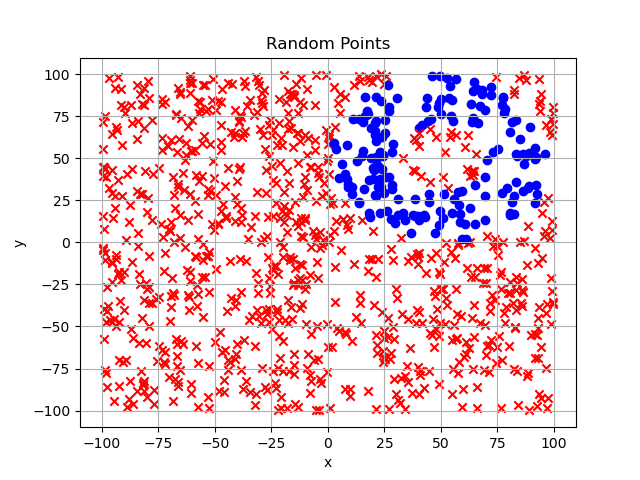
扇形(Weapon Doctrine)

rad_range関数が扇形領域の定義です。たとえば自機の進行方向から任意角度以内の別機の有無など判定できます。
Haskell:

normalize :: Point -> Point
normalize (x, y) = (x / mag, y / mag) where
                        mag = sqrt $ x^2 + y^2

dot :: Point -> Point -> Float
dot (x1, y1) (x2, y2) = x1 * x2 + y1 * y2

rad_range :: Point -> Radian -> Region  
rad_range vec_head rad_range =
    \vec_target -> 
        let
            rad_target = acos $ dot vec_head_n vec_target_n
            vec_head_n = normalize vec_head
            vec_target_n = normalize vec_target
        in rad_range >= rad_target 

Python:

def dot(p1: Point, p2: Point) -> float:
    x1, y1 = p1
    x2, y2 = p2
    return x1 * x2 + y1 * y2

def rad_range(vec_head: Point, rad_range: float) -> Region:
    def inner(vec_target: Point) -> bool:
        vec_head_n = normalize(vec_head)
        vec_target_n = normalize(vec_target)
        ratio = dot(vec_head_n, vec_target_n)
        ratio = min(1.0, max(-1.0, ratio))
        rad_target = math.acos(ratio)
        return rad_range >= rad_target
    return inner

点群処理結果：(x:50,y:50)から左下角度以内に範囲を指定しています。

let rr1 = rad_range (-1.0, -1.0) 1.0
let rel_pos = diff2D (x,y) (50.0, 50.0)
let result = rel_pos `inRegion` rr1

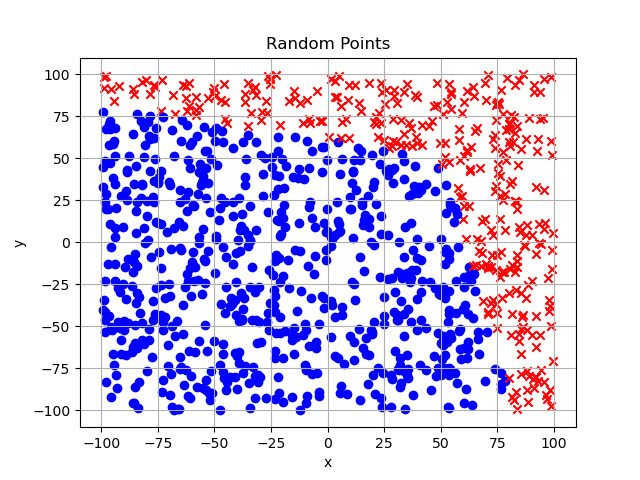
中空円と扇形の重ね合わせ

章題のとおり重ね合わせた領域を定義してみましょう。annulus同様に以下のように出来てしまいます。
Haskell:

let annu_rrange = (annulus 20 150) /\ (rad_range (-1.0, -1.0) 1.0)

Python:

annu_rrange = and_region(annulus(20, 150), rad_range((-1.0, -1.0), 1.0))

数を扱う様に領域(ラムダ式)を扱えていますね。

これをPythonかつラムダ式無しでやろうとした場合は以下のようになります。

result = in_annulus_monolis(p_rel, 20, 150) and in_rad_range((-1.0, -1.0), p_rel, 1.0)

別に悪い気はしませんね。
ではこの演算処理を、入力点のみ違えて個別の複数行でやりたい場合はどうでしょうか。
前者の場合は単にannu_rrange((x, y))をコピペして対応出来ます。ラムダ式無しのresult = in_annulus_monolis...はそのまま書く必要があります。まあこれが面倒な場合は仕方なしに以下の様にラムダ式を定義すればよいのですが。

annu_rrange = lambda p_rel: in_annulus_monolis(p_rel, 20, 150) and in_rad_range((-1.0, -1.0), p_rel, 1.0)

実際これで十分なのかもしれません。

点群処理結果：
左下への角度範囲でなおかつ距離の領域を絞って検出しています。

let rel_pos = diff2D (x,y) (50.0, 50.0)
let result = rel_pos `inRegion` annu_rrange

まとめ

結果ほとんどラムダ式に関する内容のみになったんですが、HaskellでもPythonでも、関数型的に書くことは若干有利に働く場面は確かに在ることが体感できました。行数が少なくなるかは場合によると思いますが、今回Regionという概念を数値データと同様に扱えたことはコードを書く際も見る際も自然に認識できるため良いことだった様に感じます。