学ロボでもデータ駆動型制御！（ブラシ付きDCモータの速度制御編）

はじめに

この記事は、学ロボ Advent Calendar 2023の14日目の記事です！面白かったらぜひ拡散してください！
https://adventar.org/calendars/8926

自己紹介

横浜国立大学 B3のnaokichiと申します！NHK学生ロボコン2023ではリング投擲ローラーの制御・回路などを担当しておりました！Twitterぜひフォローしてね！！
https://twitter.com/4869naokichi

この記事の概要

• 自分自身の勉強も兼ねてデータ駆動型制御（概要から実装まで）についてまとめてみた。
• 今回は学ロボでも登場頻度のそれなりに高いであろう、「ブラシ付き直流モータの速度制御」を対象としてみました。
• 学ロボでも制御工学は役に立つということをお伝えしたい！
• MATLAB/Simulinkを布教したい！

データ駆動型制御の超大ざっぱな説明

データ駆動型制御は、制御対象を完全にブラックボックスとしたまま入出力データのみを用いて制御を行う、比較的新しい制御手法です。データ駆動型制御の中にもいくつかの手法が存在します。

• IFT
• VRFT
• FRIT

今回はこれらのうち、お手軽に試せるVRFTを用いてブラシ付き直流モータの速度制御を行ってみます。理論の完全理解はひとまずおいておいて、アルゴリズムに従って実際に実装してみることを第一に目指します。理論の詳しい部分については他の文献を参照してみてください。

VRFTの超大ざっぱな説明

制御の目的は実際の応答が所望の応答にできるだけ近くなるようにすることです。これは次の評価関数$J_\text{MR}(\bm\rho)$の最小化問題に帰着できます。

$$J_\text{MR}(\bm\rho) = \left|\left|\left(\dfrac{P(z)C(z,\bm\rho)}{1+P(z)C(z,\bm\rho)} - M(z)\right)W(z)\right|\right|_2^2$$

文字	説明
規範モデル$M(z)$	所望の閉ループ伝達関数
周波数重み$W(z)$	評価したくない周波数でゲインが下がる伝達関数
制御器の構造$\bm\beta(z)$	制御器の次数などを決める

ここで、$\bm\rho$は制御器パラメータです。制御器$C(z,\bm\rho)$と$C(z,\bm\rho) = \bm\rho^\top\bm\beta(z)$の関係があります。理論的な説明はここでは省略しますが、$J_\text{MR}(\bm\rho)$の最小化は次の$J_\text{VR}(\bm\rho)$の最小化と漸近的に等価になります。

$$J_\text{VR}(\bm\rho) = \dfrac{1}{N}\sum_{t=1}^N \left(u_L(t) - \bm\rho^\top\bm\varphi(t)\right)^2$$

ここで、時系列データ$u_L(t)$と$\bm\varphi(t)$はフィルタ$L(z)$を用いて以下で生成できます。

$$u_L(t) = L(z)u_0(t)\\y_L(t) = L(z)y_0(t)\\e_L(t) = \left(M^{-1} - 1\right)y_L(t)\\\bm\varphi(t) = \bm\beta(z)e_L(t)$$

$J_\text{VR}(\bm\rho)$は制御器パラメータ$\bm\rho$に対して線形なので、最小二乗法を用いて最適なパラメータを求めることができます。

実験機器など

今回用いた機器などです。

• ブラシ付き直流モータ：RZ-735VA
• モータードライバ：自作（記事）
  • 普通のHブリッジ
  • マイコン：NUCLEO-F303K8
• ロータリーエンコーダ：AMT102
  今回用いた実験機器。モータードライバを用いて電圧を（デューティ比を）ディジタル制御することができる。また、モータのケツにロータリーエンコーダが付いており、ロータ角速度を計測することができる。
• MATLAB R2023b
  • Control System Toolbox
• STM32CubeIDE 1.14.0

MATLAB/Simulink

MATLABは様々な機能を備えた数値解析ソフトウェアです（というかプログラミング言語であり、ソフトウェア自体がIDEの体をなしている）。行列計算とかに強いです。PythonでNumPyなんかを使ったことがある人は馴染みやすいと思います。NumPyとかに比べると可読性が高いです。さらに、「ツールボックス」というアドインのようなものを追加することで様々な機能を追加することができます。

• 信号処理
• 機械学習
• 画像処理
• CUDAを用いたGPU計算
• SLAM
• 物理シミュレーション
• などなど、この他にもいっぱい……

思いつきそうなやつはだいたいツールボックスとして揃っています。SimulinkはMATLABと一緒に使う、シミュレーションに便利なシステムというかソフトです。ブロック線図を用いて直感的にシミュレーションを行うことができます。MATLAB/Simulinkはロボコンにおいてもいろいろな場面で便利に使えると思います。ロボコンのようなプロジェクトに取り組んでいる団体であれば、無料でライセンスを使用させてもらえます（加えてこのライセンス、使えるツールボックスがドチャクソ多い）。今も変わってなければ京都工芸繊維大学ForteFibreさん経由でMathWorksの方につないでもらえるはずです。ご興味があればぜひ。

設計仕様の決定

規範モデル

規範モデル$M(s)$は、閉ループ系の所望の応答を表す伝達関数です。今回は規範モデルとして次の一次遅れ系を採用しました。

$$M(s) = \dfrac{\omega_c}{s + \omega_c}$$

ここで、$\omega_c$は調整パラメータです。規範モデルの応答が早すぎる（$\omega_c$がデカすぎる）とパラメータの算出がうまくいきません。後から調整することになりますが、今はひとまず$\omega_c = 75$ rad/sとしておきましょう。規範モデルとして二次遅れ系を設定してみるのも良いでしょう。

制御器の構造

今回はPID制御を行いますので、制御器構造$\beta(z)$は以下とします。

$$\beta(z) = \begin{bmatrix}1 & \dfrac{z}{z-1} & \dfrac{z-1}{z}\end{bmatrix}^\top$$

フィルタ

$J_\text{VR}(\bm\rho)$の最小化が$J_\text{MR}(\bm\rho)$の最小化になるとは限らないので、$J_\text{VR}(\bm\rho)$に何らかのフィルタリングを施す必要があります。ここでは次の簡単なフィルタを用いることにします。

$$L(z) = M(z)(1 - M(z))$$

入出力データの取得

今回は次のようなステップ応答のデータを入出力データとして用いました。
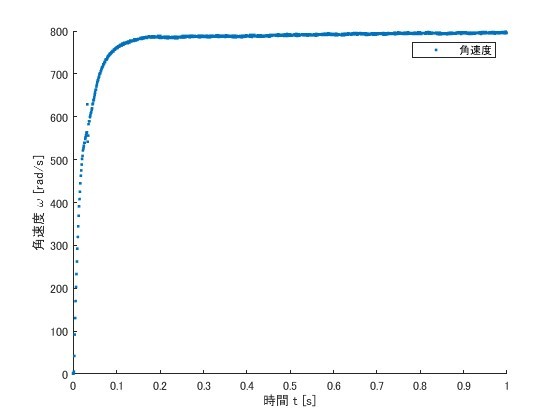ステップ応答のデータ。デューティ比 [‰]が入力データで、ロータ角速度 [rad/s]が出力データ。入力データをプロットし忘れていますが、時刻0でステップ入力を与えています。
Pゲイン小さめのP制御のデータなども利用可能かと思われますが、ステップ応答のデータを用いるのが楽かなと思います。（MATLAB、こういうグラフのプロットにも便利だよ！）

アルゴリズムに従ってPIDゲインの算出

VRFTのアルゴリズムに従ってPIDゲインを算出します。

1. 入出力データをフィルタに通す
2. 最小二乗法を解いて最適なパラメータを算出

今回、これらの処理を行うのにMATLABを用いました。\演算子を使って簡単に最小二乗解を求めることができます。MATLABのソースコードを次に示します。

myVRFT.m

clear
clc

Ts = 0.001; % 制御周期
s = tf('s');
z = tf('z', Ts);

% 規範モデル
omega_c = 75;
M = c2d(omega_c / (s + omega_c), Ts);

% 制御器構造（PID制御器）
beta = [1; Ts / (1 - z^-1); (1 - z^-1) / Ts];

% フィルタ
L = M * (1 - M);

% 入出力データ
data = csvread('step_response.csv');
u0 = data(:, 3); % 入力データ（デューティ比 [‰]）
y0 = data(:, 2); % 出力データ（ロータ角速度 [rad/s]）

% 計算
ul = lsim(L, u0);
el = lsim(L * (M^-1 - 1), y0);
phi = lsim(beta, el);
rho = phi\ul

別にPythonとかでもできると思います。このスクリプトを実行すると今回は以下のようなパラメータが得られました。

$$K_P = 0.0983, \quad K_I = 22.2021, \quad K_D = 0.0$$

マイコン上に実装

ディジタルPID制御器をマイコン上に実装します。以下は今回用いたSTM32CubeIDE用プロジェクトのリポジトリです。
https://github.com/4869naokichi/DCM_VRFT
実際にPID制御を行う部分はCore/Src/main.c内のPID()関数です。タイマー割り込みを用いてこの関数を一定の制御周期（今回は1ms）で呼び出しています。制御周期が一定でないとめちゃくちゃになってしまう（∵PIDゲインは制御周期に依存する）ので、タイマー割り込み等を用いて必ず一定周期になるようにします。

main.c

/**
 * @brief PID制御器
 * @param input 入力（制御量の現在値）
 * @param ref 目標値
 * @return 操作量
 * @note 離散化には後退オイラー法を使用
 */
float PID(float input, float ref)
{
    const float KP = -0.013255f;
    const float KI = 0.011235f;
    const float KD = 0.178028f;
    const float T_ctrl = 0.001f;

    static float ierror;
    static float derror;

    float error = ref - input;
    ierror += error;
    derror = error - derror;

    float output = KP * error + KI * ierror + KD * derror;
    
    derror = error;

    return output;
}

「制御周期をどれくらいにするか？」ですが、これに関する指標は自分もよくわかっていません。ただ、制御周期が短ければ短いほど性能も良くなるはずですので、1ステップの計算が終えられる程度に短い時間を設定するようにしています。（今回は計算部分だけだと5us程度で終わるのですが、データを文字列にして出力するのに700usくらいかかってしまうようだったので、制御周期を1msとしていました。）

実機で実験

得られたパラメータを用いて実機で実際にPID制御を行ってみましょう。以下のような結果が得られました。

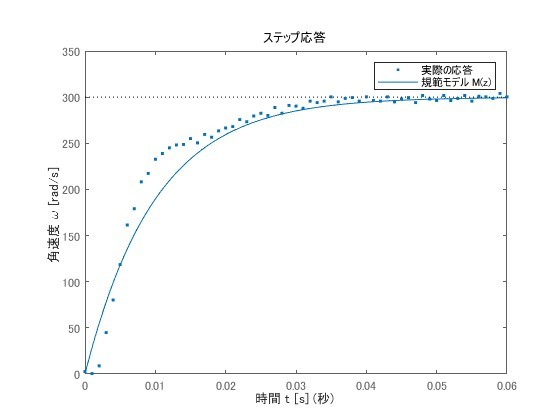
規範モデルとだいたい一致した応答が得られていることがわかります。いい感じですね。あとは応答を見ながらパラチュンがうまくいく範囲で規範モデルの応答を早く（$\omega_c$をデカく）していくことになります。

二次遅れ系でもやってみる

規範モデル$M(s)$を二次遅れ系にしてもやってみましょう。ここでは規範モデルとして次のような二次遅れ系を用います（重解、臨界減衰な応答）。

$$\dfrac{1}{(Ts + 1)^2}$$

ここで、$T$は時定数です。これは後から調整するパラメータですが、今はひとまず$T = 0.01$ sとしておきましょう。入出力データは先ほどと同じステップ応答のデータを用います。規範モデルを二次遅れ系に変更した、次のMATLABスクリプトに入出力データをぶちこみます。

myVRFT.m

clear
clc

Ts = 0.001; % 制御周期
s = tf('s');
z = tf('z', Ts);

% 規範モデル
T = 0.01;
M = c2d(1 / (T*s + 1)^2, Ts);

% 制御器構造（PID制御器）
beta = [1; Ts / (1 - z^-1); (1 - z^-1) / Ts];

% フィルタ
L = M * (1 - M);

% 入出力データ
data = csvread('step_response.csv');
u0 = data(:, 3); % 入力データ（デューティ比 [‰]）
y0 = data(:, 2); % 出力データ（ロータ角速度 [rad/s]）

% 計算
ul = lsim(L, u0);
el = lsim(L * (M^-1 - 1), y0);
phi = lsim(beta, el);
rho = phi\ul

この結果、次のようなPIDゲインが得られました。

$$K_P = 0.4679, \quad K_I = 41.7736, \quad K_D = 0.0$$

このパラメータを用いて実機で実際にPID制御を行ったところ、次のような結果が得られました。

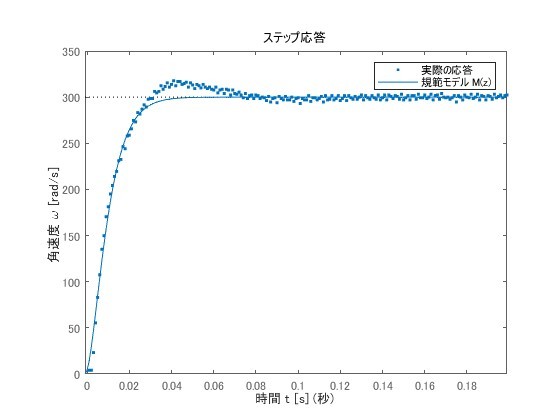
およそ合っているようにも見えますが、実際の応答では若干オーバーシュートしていますね。規範モデルを臨界減衰のやつにしたのが良くなかったのかな。

角度制御について

今回は速度制御を行ってみたわけですが、学ロボにおいては角度制御もしばしば登場します。しかし、VRFTを用いて角度制御のパラメータチューニングを行うのは意外と難しいみたいです。いろいろ検討してみましたが無理でした。いけそうになったら追記します。

参考文献

Virtual Refrence Feedback Tuning (VRFT): a new direct approach to the design of feedback controllers
↑VRFTの最初の論文
https://qiita.com/larking95/items/70f88b30072e720f58d9

おわりに

みんなもデータ駆動型制御、やろう！あとMATLAB/Simulink使おう！「学ロボで制御理論とかいらんやろwww」とかぜひ言わないでね！制御屋さんが泣くから！