📐
ABC207 D Congruence PointsをPythonと複素数で解く
問題
方針
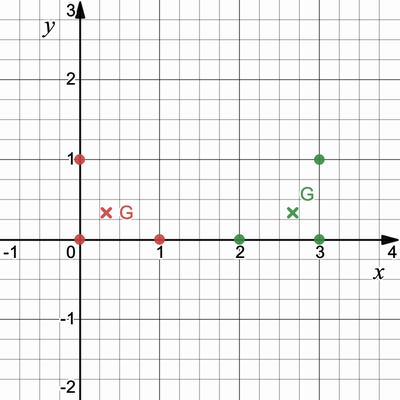
-
S -
T -
S T \overrightarrow{v_{ST}} S \overrightarrow{v_{ST}} S - 移動後の
S T G
- 移動後の
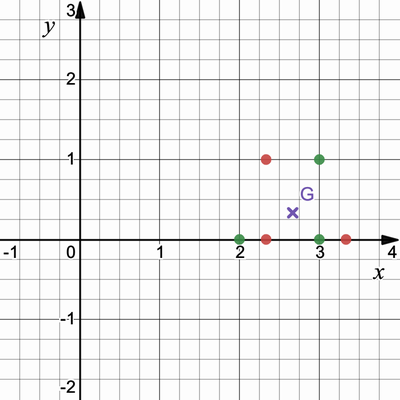
-
S T S G - これをすべての組み合わせで試す。回転後の
S T Yesであり、すべての組で試して一致しなければNoである。 -
N \leq 100
- これをすべての組み合わせで試す。回転後の
実装
import math
import cmath
import sys
from fractions import Fraction
# 標準入力
N = int(input())
S = [list(map(int, input().split())) for _ in range(N)]
T = [tuple(map(int, input().split())) for _ in range(N)]
# 重心
s_g = [Fraction(0), Fraction(0)]
t_g = [Fraction(0), Fraction(0)]
for i in range(N):
s_g[0] += S[i][0]
s_g[1] += S[i][1]
t_g[0] += T[i][0]
t_g[1] += T[i][1]
s_g[0] /= N
s_g[1] /= N
t_g[0] /= N
t_g[1] /= N
# 移動
vec_st = [t_g[0] - s_g[0], t_g[1] - s_g[1]]
for i in range(N):
S[i][0] += vec_st[0]
S[i][1] += vec_st[1]
# 回転中心の複素数
g_complex = complex(t_g[0], t_g[1])
# Tのin判定用
T_set = set(T)
# s, tを1組選ぶ
for s in S:
for t in T:
# 回転角thetaを求める
s_complex = complex(s[0], s[1])
t_complex = complex(t[0], t[1])
if s_complex == g_complex:
if s_complex == t_complex:
theta = 0
else:
continue
else:
theta = cmath.phase((t_complex - g_complex) / (s_complex - g_complex))
# Sを全てtheta回転する
for i in range(N):
s_rotated_complex = (complex(S[i][0], S[i][1]) - g_complex) * cmath.rect(1, theta) + g_complex
s_rotated = [s_rotated_complex.real, s_rotated_complex.imag]
# 整数に丸める
if math.ceil(s_rotated[0]) - s_rotated[0] < 0.0001:
s_rotated[0] = math.ceil(s_rotated[0])
if s_rotated[0] - math.floor(s_rotated[0]) < 0.0001:
s_rotated[0] = math.floor(s_rotated[0])
if math.ceil(s_rotated[1]) - s_rotated[1] < 0.0001:
s_rotated[1] = math.ceil(s_rotated[1])
if s_rotated[1] - math.floor(s_rotated[1]) < 0.0001:
s_rotated[1] = math.floor(s_rotated[1])
if not tuple(s_rotated) in T_set: # 回転後の点が元のTに含まれていなければ
break
else: # forが最後まで回ったら
print("Yes")
sys.exit()
print("No")
標準入力
listに、inを使うためにsetに変換するのでtupleにします。
N = int(input())
S = [list(map(int, input().split())) for _ in range(N)]
T = [tuple(map(int, input().split())) for _ in range(N)]
重心を求めて移動
重心は以下の式で求められます。
除算は怖いのでfractions.Fractionを使います。[1]
s_g = [Fraction(0), Fraction(0)]
t_g = [Fraction(0), Fraction(0)]
for i in range(N):
s_g[0] += S[i][0]
s_g[1] += S[i][1]
t_g[0] += T[i][0]
t_g[1] += T[i][1]
s_g[0] /= N
s_g[1] /= N
t_g[0] /= N
t_g[1] /= N
vec_st = [t_g[0]-s_g[0], t_g[1]-s_g[1]]
for i in range(N):
S[i][0] += vec_st[0]
S[i][1] += vec_st[1]
回転して一致するか試す
ここで座標を複素数に変換します。complex型では有理数や固定少数点数が使えないようなので、変換後の点が一致する場合に座標の値が整数になることを利用して、差が十分小さい時に値を丸めることにします。
複素数平面において、複素数
よって
# 回転中心の複素数
g_complex = complex(t_g[0], t_g[1])
# Tのin判定用
T_set = set(T)
# s, tを1組選ぶ
for s in S:
for t in T:
# 回転角thetaを求める
s_complex = complex(s[0], s[1])
t_complex = complex(t[0], t[1])
if s_complex == g_complex:
if s_complex == t_complex:
theta = 0
else:
continue
else:
theta = cmath.phase((t_complex - g_complex) / (s_complex - g_complex))
# Sを全てtheta回転する
for i in range(N):
s_rotated_complex = (complex(S[i][0], S[i][1]) - g_complex) * cmath.rect(1, theta) + g_complex
s_rotated = [s_rotated_complex.real, s_rotated_complex.imag]
# 整数に丸める
if math.ceil(s_rotated[0]) - s_rotated[0] < 0.0001:
s_rotated[0] = math.ceil(s_rotated[0])
if s_rotated[0] - math.floor(s_rotated[0]) < 0.0001:
s_rotated[0] = math.floor(s_rotated[0])
if math.ceil(s_rotated[1]) - s_rotated[1] < 0.0001:
s_rotated[1] = math.ceil(s_rotated[1])
if s_rotated[1] - math.floor(s_rotated[1]) < 0.0001:
s_rotated[1] = math.floor(s_rotated[1])
if not tuple(s_rotated) in T_set: # 回転後の点が元のTに含まれていなければ
break
else: # forが最後まで回ったら
print("Yes")
sys.exit()
print("No")
Discussion