😸

OpenQASM 3. フワッと解説

に公開
assembly
quantum
tech

このページの目的

  • このページはOpenQASM3. をフワッと説明するページである。
  • 量子力学の基礎とかゲート操作とか知ってる人向け。

OpenQASM 3. とは

  • OpenQASM3. とは、量子計算機のアセンブリ言語 OpenQASMのバージョン3.である。
  • この論文を見ればだいたいわかる。

例を見る

論文6章で取り上げられていた反復位相推定アルゴリズムをステップバイステップで見てみる。論文中の物のほうが色分けされてて見やすいが・・・。

OPENQASM 3;
include "stdgates.inc"
  • OPENQASM 3 OpenQASM3.のコードであることを表現している。
  • include "stdgates.inc" stdgates.inc をincludeしていることを表現している。
const n = 3; // number of iterations
const θ = 3 * π / 8; // phase angle on target qubit
  • 古典的な定数 n と Θ を宣言している。
qubit q; // phase estimation qubit
qubit r; // target qubit for the controlled-unitary gate
angle[n] c = 0; // phase estimation bits
  • 量子ビット q と r および angle[n] 型の c を宣言している。 angle[n] 型については下参照。
// initialize
reset q;
reset r;
// prepare uniform superposition of eigenvectors of phase
h r;
  • 量子ビット q と r を \ket{0} で初期化している。
  • アダマールゲート H を r に適用している。
// iterative phase estimation loop
for k in [1:n] { // implicitly cast val to int
  • for 文で、 k が 1 から n になるまで1増やしつつ {} 内ループ。
reset q;
h q;
  • q を \ket{0} に
  • H を q に適用。
ctrl @ pow(2**k) @ phase(θ) q, r;
  • ctrl @ gate は対象の gate をコントロールゲートにする修飾子。修飾子とは、下を参照。
  • pow(K) @ gate は対象の gate を K 回作用させるようにするゲートにする修飾子。
  • phase(Θ) はZ軸でのΘ回転させるゲート。
inv @ phase(c) q;
  • inv @ gate は対象の gate の逆を作用させるようにするゲート。つまり、gate の作用がユニタリー作用素 U だった場合は、 U^* を作用させるようになる修飾子。
h q;
measure q -> c[0];
// newest measurement outcome is associated to a π/2 phase shift
  • measure q-> c[0] 量子ビット q を測定して c[0] に結果を格納する。
// in the next iteration, so shift all bits of c left
c <<= 1;
}
  • c <<= 1 cを初期化(1に)する。
// Now c contains the n-bit estimate of ϕ in the
// eigenvalue e^{i*ϕ} and qreg r is projected to an
// approximate eigenstate of the phase gate.

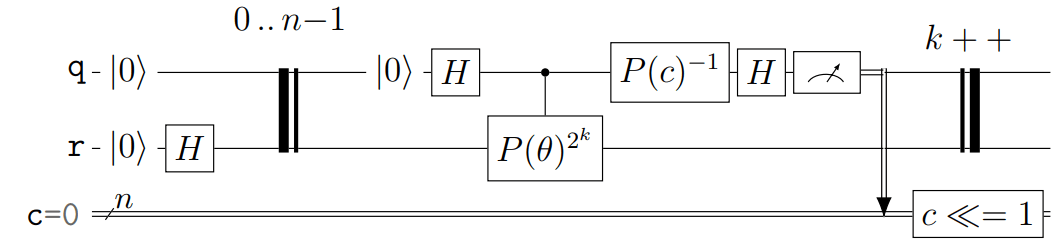
このコードで生成される回路図が次のようになる。この図は論文中から拝借した。
回路

出てきた命令たち

例で出てきた命令たちについてまとめると次のようになる。

宣言

  • const n = x; 古典定数の n を左辺値で初期化して宣言する。
  • qubit q; 1量子ビットの q を宣言する。
  • angle[n] c = 0; angle[n] 型の変数 c を 0 で初期化して宣言する。
  • gate cx c, t { ctrl @ x c, t; } cx ゲートを引数 c, t として持ち、 ctrl @ x を c, t に対して適用するゲートとして宣言する。
  • gate phase(λ) q { U(0,0,λ) q; } 古典引数 λ を用いてゲートを定義する方法もある。

関数

  • reset q; 量子変数 q を \ket{0} に初期化する。
  • h r; アダマールゲート H を量子変数 r に作用させる。
  • measure q -> c[k] 量子変数 q を測定し、古典型の angle[n] 型である c の k 番目に代入する。
  • c <<= 1 型 angle[n] の古典変数に対して作用して、c_n をすべて 1 にする。

文

  • for k in [1:n] { P } 文 P を k を 1ずつ増加させつつ n になるまで実行する。

修飾子

  • ctrl @ g コントロール修飾子: 作用素 g を作用させるゲート g に対して作用し、I\oplus g を作用させるコントロール g ゲートとなる。ここでこの I の次元は g と同じ。
  • pow(X) @ g べき乗修飾子: g を X 回作用させる。 X は非整数でも可能で、その場合は g = \exp(iH) をみたすとき pow(X) @ g = \exp(iXH) である。
  • inv @ g 逆関数修飾子: ゲート g が g を作用させる時、その逆 g^* を作用させるゲートになる。

型

出てきた謎の型についての説明。

古典型

  • angle[n] x n個の0または1の列 \{c_n\} によって以下のように表される [0,2\pi) の有利数値。
    x = 2\pi \cdot 0.c_{n-1}c_{n-2}\cdots c_0.

    (注: 0.c_{n-1}c_{n-2}\cdots c_0 = \sum_{j=0}^{n-1}2^{-n+j}c_j.)

補遺

ここで紹介していない命令もいっぱいあるので、論文を確認のこと。

紹介していない機能の一例:

  • delay[t] q
  • box{ P }
  • box[t]{ P }
  • barrier r, q

OpenQASMはコヒーレンス時間とかの制約から素の文からさらに様々な最適化をすることが必要なので、古典計算機でいう意味のアセンブリ言語とは少し異なる立ち位置にある。

Discussion