Zenn
🍔

ボードゲームの最適解を探索してみる〈ナインタイルパニック〉

2022/12/17に公開
Python
ゲーム
#
ボードゲーム
tech

この記事は、Oink Games が販売する「ナインタイルパニック」というゲームの最適解を探すプログラムについての備忘録です。
このプログラムは、テクニカルな計算時間の短縮や並列計算を行わず、探索対象の性質を考慮して全探索の数を削減しています。
そのため、アルゴリズムの目新しさなどはありません。

「いそげ、脳みそ。」

ナインタイルパニックの箱裏のキャッチコピーです。どんなゲームかを端的に表しています。
ルールの詳細は実際にゲームを買って遊ぶのが理解への近道ですが、購入するまでは公式サイトの説明を読んでみてください。

簡単に言うと、

  • プレイヤーが全員同じタイルを持ち、個人で競う
  • 毎回ランダムで変わる 3 つのお題をなるべく満たすようにタイルを並べる
  • お題ごとに点数を計算して、順位を決める（同率は先着順）
  • タイルを並べるのは時間制限がある

という性質のゲームです。
お題の組合せによっては、3 つすべてで最高得点を取ることができるかもしれません。
そのため、全てのタイルの並べ方（「町」と呼ばれます）に対して、全てのお題の点数を計算することで、理論上は最適解が見つかるはずです。

結論

お題セットごとに最高得点を取れる町

3 つのお題すべてでそれぞれの最高点を取れるお題セットについては、お題セットごとの最適解（最高得点）にてコードと町のリストを記載しています。

3 つのお題のうちどれかで最高得点を取れないにしろ、そのお題セットでの最適解は存在します。
こちらはお題セットごとの最適解（総当たり）に手法を記載しています。
そして、最適解の最小解の結果、少なくとも 429 の町で 2,600 のお題セットの最適解を満たせることが分かりました。
たとえば、以下の町は 86 のお題セットについて最適解となります。全てのリストはナインタイルパニックの最適解にまとめました。
town: 036582714004421544

26 のお題について、最高得点からの距離が短い町

お題セットを考えず、全てのお題について最高得点に近い町を探索することもできます。
全てのお題についての距離は、199-681 の範囲（200, 201, 203, 673, 678, 680 は除く）を取りました。
距離が 199 であるお題シノニムは 1 つで、そのリストは以下でした。

Theme synonym ID = 1547940
0, 0, 3, 0, 10, 9, 4, 12, 1, 3, 1, 3, 2, 1, -3, 4, 3, 3, 3, 0, 6, 2, 4, 3, 2, 1

583201764425441001
583201764425441011
583271064425411701
583271064425411711

最高得点となるお題の数が多い町

探索の結果、同時に最高得点となれるのは 7 つのお題までで、該当するお題シノニムは 2 つ、7 つのお題とはともに、4, 9, 11, 14, 22, 24, 26 でした。
それぞれのお題シノニムとその町パターンのリストは以下でした。

Theme synonym ID = 2004525
1, 0, 1, 0, 4, 3, 2, 1, 5, 3, 3, 3, 1, 4, -3, 1, 2, 0, 1, 0, 7, 6, 1, 3, 3, 4

036582714004421544
036582714004421564
036582714006421544
036582714006421564
306582714004421544
306582714004421564
306582714006421544
306582714006421564
057381624044025515
057381624044027515
057381624044025715
057381624044027715
357081624044025515
357081624044027515
357081624044025715
357081624044027715

お題 16 だけ 1 から 0 点に変わります。

Theme synonym ID = 2004522
1, 0, 1, 0, 4, 3, 2, 1, 5, 3, 3, 3, 1, 4, -3, 0, 2, 0, 1, 0, 7, 6, 1, 3, 3, 4

036582714004421545
036582714004421565
036582714004421744
036582714004421745
036582714004421764
036582714004421765
036582714006421545
036582714006421565
036582714006421744
036582714006421745
036582714006421764
036582714006421765
306582714004421545
306582714004421565
306582714004421744
306582714004421745
306582714004421764
306582714004421765
306582714006421545
306582714006421565
306582714006421744
306582714006421745
306582714006421764
306582714006421765
057381624044025514
057381624044027514
057381624044025714
057381624044027714
057381624046025514
057381624046025515
057381624046027514
057381624046027515
057381624046025714
057381624046025715
057381624046027714
057381624046027715
357081624044025514
357081624044027514
357081624044025714
357081624044027714
357081624046025514
357081624046025515
357081624046027514
357081624046027515
357081624046025714
357081624046025715
357081624046027714
357081624046027715

町の得点を計算する探索アルゴリズムを考える

愚直な順に 3 種類列挙します。各アルゴリズムの最後に、パターンとその点数を出力するコードを記載します。

アルゴリズム A：全探索

全てのパターンを探索するアルゴリズムです。
9 枚のタイルの表裏（8^2 = 64 通り）、角度（8^4 = 4096 通り)、およびそのタイルを置く場所（9! = 362880 通り）の積の 48,704,929,136,640 通りがあります。
この探索アルゴリズムを初めに作成した当初（2022 年 9 月）は、町が完成できるかどうかだけを探索していました。
しかし、筆者の環境では、秒速 2700 通り程度しか探索できず、単純計算で約 572 年 (!) かかるため、コンピュータお姉さんになっていまいます。

from nine_tiles_panic import Search, Town
for pattern in Search.search_all():
    points = Town(pattern).get_theme_point()
    print(pattern, points)

アルゴリズム B：道の形状だけ先に探索する

道の形状だけに着目して町を完成できるか探索して、その次に、タイルを当てはめるアルゴリズムです。
アルゴリズム C は点数計算を省力化するアルゴリズムなので、現時点での町の探索法で最も短いのはアルゴリズム B です。

コード中では、道の形状が同じタイルを "道シノニム (road synonym)"、道の形状が同じ町を "町シノニム (town synonym)" と表しています。
完成している町とは、公式サイトによると、「３✕３の範囲の中で自由に入れ替え、向きを変えたり、裏返したりして、きちんと道がつながった町」であるとされています。実際は、町の中で閉路を作ってはいけないという制約も追加されます。

探索の上での工夫として、各タイルや町全体を回転して道の形状が同じになるパターンを除外しました。また、元のタイルの表裏を合わせても足りない枚数の組合せになる町シノニムも除外しました。このアルゴリズムでの探索の結果、63,660 通り（一覧）が見つかりました。筆者の環境では、約 20 時間で探索が終わりました。

from nine_tiles_panic import Search
for _ in Search.search_synonym("synonym_pattern.txt"):
    pass

ここで、このプログラムにおける町パターンの記述方法を説明します。
町パターンの記法は、18 桁の 0-9 からなる数字列で、前半 (position) と後半 (direction) に分けられます。
例えば、町シノニムの 224221113000100031 は以下の形状です。

from nine_tiles_panic import Tile, Town, View
View(Town("224221113000100031", Tile.get_synonym())).draw()

"tow synonym: 224221113000100031"

説明のために、タイル位置の番号も描画します。タイルの左上に [] で囲まれた数字が位置番号です。（裸の 0-3 の数字は、後述する道の辺番号です。）

from nine_tiles_panic import Tile, Town, View
View(Town("224221113000100031", Tile.get_synonym()), view_number=True).draw()

"tow synonym with number: 224221113000100031"

前半の 224221113 は、その index の位置にあるタイルの種類を表しています。例えば 0 桁目の 2 は、曲線が 2 つあるタイルが 0 番目の位置（町の左上）にあることを表しています。
道シノニムの番号はプログラム中の Tile.get_synonym() で定義されていますが、図示すると以下の 5 種類です。十の位がタイルの種類を表しています。

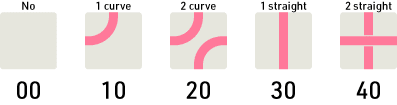
road synonyms

後半の 000100031 は、その index の位置にあるタイルの方向を示しています。0 は上図の向きを表し、1 増える毎に左に 90 度回転することを示します。例えば、3 桁目の 1 は、3 番目の位置（町の左）にある 2 のタイルが 1 の向き、即ち左 90 度回転していることを表しています。

町パターンの記法はここまでです。
こうして "生成可能な" 町シノニムのパターンが得られたので、あとは元のタイルセットの表裏の組合せを考慮して "実際に" 作成可能な町かどうかを判定すればいいことになります。

そのために、上で得られた synonym_pattern.txt を基に以下のコードを使って、生成可能な町とその点数を計算できます。
このコードでは、タイル上のオブジェクトを考慮して、自明に同じ点数になるタイルの向きを除外するよう工夫しました。このゲームでは、以下の 3 種類の性質のオブジェクトが得点計算に関わってきます。

  • 道の向きとオブジェクトの向きが関係する：エージェント（道の上）、宇宙人（道の上）
  • 道の向きのみ関係する：ハンバーガー
  • 向きは関係しない：犬、市民（女の子）、市民（男の子）、家、UFO、エージェント（道の外）、宇宙人（道の外）

探索の結果、実際に完成できる町は（コードが正しければ）526,070,976 通りです。

from nine_tiles_panic import Search
with open("synonym_pattern.txt") as f:
    for line in f:
        pattern_synonym = line.split("\n")[0]
        for pattern, points in Search.search_point_from_synonym(pattern_synonym):
            print(pattern, points)

アルゴリズム C：道シノニムと、元のタイルとで段階を踏んで点数計算する

このアルゴリズムでは、お題の得点を段階的に計算することで、計算時間を短縮しました。
得点を計算する上で、以下の 4 種類のお題に分類できます。

  1. 道の上のオブジェクトから計算する：「宇宙人をつかまえた数が多い」など
  2. タイルの上の道の外のオブジェクトから計算する：「犬の数が多い」など
  3. 道の形状から計算する：「カーブの数が多い」など
  4. タイルに関係ない：「町を完成させるのが早い」

そのため、4. のお題は 0 点で固定し、町シノニムで 3. のお題を計算し、タイル面が変わらない間は 2. のお題を計算して、残りの 1. のお題を毎回の町で計算することで、計算量を削減できます。

from nine_tiles_panic import Search
for pattern, points in Search.search_point_2():
    print(pattern, points)

お題の得点を整理する

python -m nine_tiles_panic で得られた success_pattern.db に対して抽出操作すればお題やお題セットの性質を知ることができます。

お題ごとの得点

まずは、各お題でありうる得点を抽出して、その最高得点を列挙してみました。

SQL
select distinct t01 from towns; -- お題 1 のありうる得点を抽出する
お題 ありうる得点 最高得点
1 0, 1, 2, 3, 4 4
2 0, 1, 2, 3, 4 4
3 1, 2, 3, 4, 5 5
4 0 0
5 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 11
6 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 11
7 1, 2, 3, 4, 5, 6 6
8 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20 20
9 0, 1, 2, 3, 4, 5 5
10 1, 2, 3, 4, 5, 6 6
11 0, 1, 2, 3 3
12 1, 2, 3, 4, 5, 6 6
13 1, 2, 3, 4, 5 5
14 0, 1, 2, 3, 4 4
15 -6, -5, -4, -3, -2, -1 -1
16 0, 1, 2, 3, 4, 5, 6, 7 7
17 0, 1, 2, 3, 4, 6, 8 8
18 0, 1, 2, 3, 4 4
19 0, 1, 2, 3, 4 4
20 0, 1, 2, 3 3
21 1, 2, 3, 4, 5, 6, 7, 8, 9 9
22 0, 1, 2, 3, 4, 5, 6 6
23 1, 2, 3, 4, 5 5
24 0, 1, 2, 3, 4, 5 5
25 0, 1, 2, 3 3
26 0, 1, 2, 3, 4 4

お題シノニムの抽出

26 のお題全てが同じ得点となるような "お題シノニム (theme synonym)" をそれぞれファイルに切り出してみます。

import sqlite3
conn = sqlite3.connect("success_pattern.db")
cur = conn.cursor()
for town in cur.execute("SELECT * FROM towns"):
    with open("theme_synonym/{}.txt".format("_".join(map(str, town[3:]))), mode="a") as f:
        f.write(town[1].zfill(9) + town[2].zfill(9) + "\n")
cur.close()
conn.close()

これによって、1-26 のお題の得点パターンのファイルの中にその得点パターンになる町パターンが抽出されます。
抽出の結果、お題シノニムは 6,702,635 通りです。
筆者の環境では、約 4.5 日で抽出が終わりました。

お題セットごとの最適解（最高得点）

26 枚のお題カードから 3 枚をランダムに選ぶため、_{26}\mathrm{C}_3=2600 通りのお題セットが存在することになります。
その 2,600 通りの中から、3 つのお題すべてが最高得点となるような町が存在するお題セットを探索します。

import itertools
import numpy as np
import sqlite3

NUM_TILE = 9
NUM_THEME = 26
NUM_TURN = 3

dbname = "success_pattern.db"
max_points = np.asarray([4, 4, 5, 0, 11, 11, 6, 20, 5, 6, 3, 6, 5, 4, -1, 7, 8, 4, 4, 3, 9, 6, 5, 5, 3, 4])

conn = sqlite3.connect(dbname)
cur = conn.cursor()
for town in cur.execute("SELECT * FROM towns"):
    points = np.asarray(town[3:])
    distance = max_points - points
    if np.count_nonzero(distance) <= NUM_THEME - NUM_TURN:
        pattern = town[1].zfill(NUM_TILE) + town[2].zfill(NUM_TILE)
        for theme_set in itertools.combinations(np.where(distance==0)[0].tolist(), NUM_TURN):
            filename = "_".join([str(theme + 1).zfill(2) for theme in theme_set])
            with open("./theme_set/theme_{}.txt".format(filename), mode="a+") as f:
                f.write(pattern + "\n")
cur.close()
conn.close()

これによって、3 つのお題すべてが最高得点を達成するような町パターンが、お題セットごとのファイルに抽出されます。
また、お題 4 はすべて 0 点に設定しているため、実質的に 2 つのお題セットで最高得点を達成するような町パターンも抽出されています。
以下の町パターンは GitHub 上にアップロードしています。

3 つのお題すべてが最高得点となるお題セット（117 セット）
お題セット 3 つのお題すべてが最高得点となる町の数
(1, 4, 11) 696
(1, 4, 20) 1
(1, 4, 25) 2338
(1, 11, 25) 696
(2, 4, 5) 784
(2, 4, 7) 16
(2, 4, 18) 368
(2, 4, 23) 472
(2, 5, 18) 196
(2, 5, 23) 224
(2, 7, 18) 4
(2, 7, 23) 8
(2, 18, 23) 118
(3, 4, 5) 19456
(3, 4, 11) 7680
(3, 4, 12) 402816
(3, 4, 16) 192
(3, 4, 21) 1221120
(3, 11, 12) 7680
(4, 5, 6) 857088
(4, 5, 7) 373248
(4, 5, 8) 18432
(4, 5, 14) 196608
(4, 5, 15) 13824
(4, 5, 16) 168
(4, 5, 18) 4608
(4, 5, 19) 46208
(4, 5, 23) 538112
(4, 6, 7) 2442240
(4, 6, 23) 5965824
(4, 7, 15) 3072
(4, 7, 18) 3518
(4, 7, 19) 141880
(4, 7, 23) 3270976
(4, 8, 19) 166208
(4, 8, 23) 908032
(4, 9, 11) 27648
(4, 9, 14) 128256
(4, 9, 22) 27648
(4, 9, 25) 138240
(4, 9, 26) 46080
(4, 10, 23) 9216
(4, 11, 12) 13824
(4, 11, 14) 1728
(4, 11, 15) 3456
(4, 11, 17) 35592
(4, 11, 18) 18
(4, 11, 19) 3576
(4, 11, 22) 14848
(4, 11, 24) 18432
(4, 11, 25) 302976
(4, 11, 26) 46080
(4, 14, 21) 331264
(4, 14, 22) 4896
(4, 14, 25) 110528
(4, 14, 26) 8256
(4, 15, 18) 44
(4, 15, 19) 256
(4, 15, 23) 1536
(4, 15, 25) 5760
(4, 17, 18) 234
(4, 17, 19) 13112
(4, 18, 19) 11594
(4, 18, 23) 9388
(4, 19, 23) 375960
(4, 21, 25) 840704
(4, 22, 25) 523392
(4, 22, 26) 523392
(4, 24, 25) 36864
(4, 25, 26) 948224
(5, 6, 7) 248832
(5, 6, 23) 244224
(5, 7, 23) 147456
(5, 8, 19) 13824
(5, 8, 23) 5632
(5, 18, 19) 2672
(5, 18, 23) 1906
(5, 19, 23) 17632
(6, 7, 23) 946176
(7, 15, 18) 44
(7, 15, 19) 256
(7, 15, 23) 1536
(7, 18, 19) 2000
(7, 18, 23) 1913
(7, 19, 23) 69692
(8, 19, 23) 65200
(9, 11, 14) 1728
(9, 11, 22) 4096
(9, 11, 25) 27648
(9, 11, 26) 9216
(9, 14, 22) 1440
(9, 14, 25) 12864
(9, 14, 26) 2112
(9, 22, 25) 27648
(9, 22, 26) 27648
(9, 25, 26) 46080
(11, 14, 22) 64
(11, 14, 25) 1728
(11, 14, 26) 192
(11, 15, 25) 3456
(11, 17, 18) 18
(11, 17, 19) 3576
(11, 18, 19) 18
(11, 22, 25) 14848
(11, 22, 26) 14848
(11, 24, 25) 9216
(11, 25, 26) 23040
(14, 21, 25) 16512
(14, 22, 25) 4896
(14, 22, 26) 4896
(14, 25, 26) 8256
(15, 18, 19) 44
(15, 18, 23) 23
(15, 19, 23) 128
(17, 18, 19) 234
(18, 19, 23) 4789
(22, 25, 26) 523392

筆者の環境では約 45 h で抽出が終わりました。

お題の距離

お題の "距離 distance" を定義します。
お題ごとの得点の「ありうる得点」内の順位 - 1 をお題の距離とします。
例えば、お題 8 の 15 点は 4 番目なので、距離は 4-1=3 とします。
複数のお題の距離は、それぞれのお題の距離の 2 乗の和とします。

ここで、全てのお題シノニムについて、距離の 2 乗の DB (theme_synonym_distance.db) を用意します。
まずは、お題シノニムの抽出で抽出した txt ファイルのファイル名（お題シノニムの点数）をまとめておきます。

bash
ls ./theme_synonym/*.* > theme_synonym.txt

次に、全てのお題シノニムについて、最高得点との距離を計算して DB に格納します。

import sqlite3
from nine_tiles_panic import Sql

dbname = "theme_synonym_distance.db"
NUM_THEME = 26
input = "theme_synonym.txt"

points_rank = [  # それぞれのお題のありうる得点降順
    [4, 3, 2, 1, 0], 
    [4, 3, 2, 1, 0], 
    [5, 4, 3, 2, 1], 
    [0], 
    [11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1], 
    [11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1], 
    [6, 5, 4, 3, 2, 1], 
    [20, 18, 16, 15, 14, 12, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0], 
    [5, 4, 3, 2, 1, 0], 
    [6, 5, 4, 3, 2, 1], 
    [3, 2, 1, 0], 
    [6, 5, 4, 3, 2, 1], 
    [5, 4, 3, 2, 1], 
    [4, 3, 2, 1, 0], 
    [-1, -2, -3, -4, -5, -6], 
    [7, 6, 5, 4, 3, 2, 1, 0], 
    [8, 6, 4, 3, 2, 1, 0], 
    [4, 3, 2, 1, 0], 
    [4, 3, 2, 1, 0], 
    [3, 2, 1, 0], 
    [9, 8, 7, 6, 5, 4, 3, 2, 1], 
    [6, 5, 4, 3, 2, 1, 0], 
    [5, 4, 3, 2, 1], 
    [5, 4, 3, 2, 1, 0], 
    [3, 2, 1, 0], 
    [4, 3, 2, 1, 0]
    ]

conn = sqlite3.connect(dbname)
cur = conn.cursor()
# DB 初期化
cur.execute(
    "CREATE TABLE themes(\
    id integer primary key autoincrement, "
    + "num_max integer, all_dist integer, "
    + " integer, ".join(Sql.theme_cols)
    + " integer)"
)
# お題シノニムを登録（ついでに、最高得点となるお題の数 (num_max) と距離の総和 (all_dist) も計算）
with open(input) as f:
    for line in f.readlines():
        points = list(map(int, line.split(".")[0].split("_")))
        distance = [points_rank[i].index(point) ** 2 for i, point in enumerate(points)]
        sum_dist = sum(distance)
        cur.execute(
            "INSERT INTO themes VALUES(NULL, {}, {}, {})".format(
                distance.count(0), sum_dist, ", ".join(list(map(str, distance)))
            )
        )
conn.commit()
cur.close()
conn.close()

お題セットごとの最適解（総当たり）

お題セットごとの最適解（最高得点）では、3 つのお題すべてで最高得点を取れる解を探しました。
そこで、そのような解が存在しないお題セットでも最適解を探すために以下の手順で探索しました。

  1. お題セットの得点パターンを抽出
  2. 同一のお題セット内で、得点パターンを総当たりで比較し、勝利数が最多の得点パターンを抽出
import itertools
import sqlite3
from typing import List, Tuple

NUM_THEME = 26
NUM_TURN = 3
num_max_win = 6  # 一度実行してから最大数を得た

dbname = "theme_synonym_distance.db"
conn = sqlite3.connect(dbname)

with open("most_win.csv", mode="a+", encoding="utf-8_sig") as w:
    w.write("theme_set_id,n{}\n".format(",theme_set_dist_" + ",theme_set_dist_".join(map(str, range(1, num_max_win + 1)))))

    for theme_set in itertools.combinations(range(NUM_THEME), NUM_TURN):
        triplet_dist_list: List[Tuple[int]] = []  # 3 お題の距離の種類を格納
        for record in conn.execute(
            "SELECT DISTINCT {} FROM themes;".format(
                ", ".join(["t" + str(theme + 1).zfill(2) for theme in theme_set])
                )):
            triplet_dist_list.append(record)
        triplet_num = len(triplet_dist_list)  # 3 お題の種類
        # 距離セットの数を絞り込む
        while True:
            # 3 お題の距離を総当たりで戦わせて、勝利数・敗北数を格納
            triplet_dist_dict_win = dict(zip(triplet_dist_list, [0] * len(triplet_dist_list)))
            triplet_dist_dict_lose = dict(zip(triplet_dist_list, [0] * len(triplet_dist_list)))
            for triplet0, triplet1 in itertools.combinations(triplet_dist_list, 2):
                num_win = [0, 0]
                for dist0, dist1 in zip(triplet0, triplet1):
                    if dist0 < dist1:
                        num_win[0] += 1
                    elif dist0 > dist1:
                        num_win[1] += 1
                if num_win[0] > num_win[1]:
                    triplet_dist_dict_win[triplet0] += 1
                    triplet_dist_dict_lose[triplet1] += 1
                elif num_win[0] < num_win[1]:
                    triplet_dist_dict_win[triplet1] += 1
                    triplet_dist_dict_lose[triplet0] += 1
            # 最少敗北数の距離セットを取得
            min_lose_triplet_list = [kv[0] for kv in triplet_dist_dict_lose.items() if kv[1] == min(triplet_dist_dict_lose.values())]
            triplet_dist_dict_win_min_lose = {key: triplet_dist_dict_win[key] for key in min_lose_triplet_list}
            # 敗北最少中の勝利数最多の距離セットを取得
            triplet_dist_list = [kv[0] for kv in triplet_dist_dict_win_min_lose.items() if kv[1] == max(triplet_dist_dict_win_min_lose.values())]
            if len(triplet_dist_list) == 1 or triplet_num == len(triplet_dist_list):
                # 距離セットが 1 つになるか、前のループから距離セット数が変わらなかったら終了
                triplet_num = len(triplet_dist_list)
                break
            else:
                # 終了しなかったら距離セット数を更新
                triplet_num = len(triplet_dist_list)

        theme_set_id = "_".join([str(theme + 1).zfill(2) for theme in theme_set])
        w.write("{},{},{}\n".format(
            theme_set_id, 
            triplet_num, 
            ",".join(['"{}"'.format(triplet_dist) for triplet_dist in triplet_dist_list]) + "," * (num_max_win - triplet_num)
        ))
conn.close()

お題セットごとの最適解の距離の 2 乗のパターン一覧は most_win.csv に出力されています。
例えば、お題セットごとの最適解（最高得点）にあるお題セットは、ここでは全て (0, 0, 0) になっています。
また、n > 1 なお題セットでは、どの 2 つを取っても、同時に出した場合引き分けになるため複数の得点パターンが存在しています。

筆者の環境では、約 2 h で計算が終わりました。

most_win.csv を純粋な得点に戻したファイルは most_win_points.csv に出力しました。

最適解の最小解

お題セットごとの最適解（総当たり）の結果からさらに 1 段階探索します。
複数のお題セットについて最適解となれるお題シノニムも存在するので、それを覚えておけば最適解を出しやすいです。
その手順として、3. 以降は次の様になります。

  1. お題セットの得点パターンを抽出
  2. 同一のお題セット内で、得点パターンを総当たりで比較し、勝利数が最多の得点パターンを抽出
  3. 多くのお題セットの最適解となれるお題シノニムを選択
  4. そのお題シノニムが最適解となれないお題セットについて、多くの最適解となれるお題シノニムを選択
  5. 全てのお題セットについて、4. のお題シノニムを選択できるまで繰り返す
import sqlite3
import pandas as pd

df = pd.read_csv("most_win.csv", index_col=0).drop("n", axis=1)
most_win_dict = df.T.to_dict(orient="list")

for theme_set_id, triplet_dists in most_win_dict.items():
    most_win_dict[theme_set_id] = [list(map(int, triplet_dist[1:-1].split(", "))) for triplet_dist in triplet_dists if isinstance(triplet_dist, str)]

dbname = "theme_synonym_distance.db"
conn = sqlite3.connect(dbname)

with open("most_win_match.csv", mode="a+") as w:
    w.write("theme_synonym_id,n,matched_theme_set\n")
    for record in conn.execute("SELECT * FROM themes;"):
        theme_synonym_id = record[0]
        dists = record[5:]
        win_match_list = []
        for theme_set_id, win_dist_set in most_win_dict.items():  # 3 お題について、最善手の点数セット
            if theme_set_id == "04_10_15":
                win_match_list.append("04_10_15")
            else:
                theme_set = [int(theme_id) - 1 for theme_id in theme_set_id.split("_")]
                did_match = True
                for win_dist in win_dist_set:  # 最善手の得点セットについて、それぞれマッチするか確認
                    for theme_id, dist in zip(theme_set, win_dist):
                        if dists[theme_id] != dist:  # どれかでマッチしなかったらその得点セットは終了
                            did_match = False
                            break
                    if did_match:  # 全部でマッチしたらそのお題セットは終了
                        win_match_list.append(theme_set_id)
                        break
        if (num_match := len(win_match_list)) - 1:  # 04_10_15 以外の何かでマッチしたら格納
            w.write('{},{},"{}"\n'.format(theme_synonym_id, num_match, ", ".join(win_match_list)))
conn.close()

この結果、お題セット (4, 10, 15) 以外についても最適解となったお題シノニムは 2,530,458 通りでした。

筆者の環境では、約 6.5 h で most_win_match.csv が出力されました。
このファイルについてさらに以下のコードで探索しました。

# お題セット毎の最適解のお題シノニムのリストを読み込んで、matched_theme_set カラムを str から list に変換する
most_win_match = pd.read_csv("most_win_match.csv", index_col=0)
most_win_match = most_win_match[["n"]].merge(
    most_win_match[["matched_theme_set"]].apply(lambda r: r[0].split(", "), axis=1).rename("matched_theme_set"), 
    left_index=True, 
    right_index=True
    )
most_win_match_list = [most_win_match.copy()]

# 最小最適解を格納する辞書（key：お題セット、value：満たすお題シノニムの id リスト）
most_win_min: dict[str, int] = dict(zip(most_win_dict.keys(), [None for _ in most_win_dict]))

def remove_list_items(base_list:list, remove_items:set) -> list:
    """base_list から remove_items の要素を削除して、削除後のリストとその長さを返す"""
    for item in remove_items:
        try:
            base_list.remove(item)
        except ValueError:
            pass
    return len(base_list), base_list

def extract_min_match(most_win_match:pd.DataFrame):
    """最適解となるお題セットが最多のお題シノニムを特定し、そのお題シノニムが満たすお題セットを登録し、全体から削除して返す"""
    n_max = most_win_match[["n"]].max().values[0]  # 最適解になれるお題セットの数の最大値
    most_matched_synonym = most_win_match[most_win_match["n"] == n_max][["matched_theme_set"]]  # 最適解になれるお題セットが最多のお題シノニム
    most_matched_synonym = most_win_match_list[0][["n"]].merge(  # 全お題セットでの最適解マッチ数をマージ
        most_matched_synonym, how="inner", left_index=True, right_index=True
        ).sort_values(by="n", ascending=False)
    most_matched_synonym.to_csv("most_win_match/most_win_match_{}_{}.csv".format(
        n_max, best_match_synonym := most_matched_synonym.index.values[0]
            )
        )
    print(n_max, best_match_synonym, sep="\t")

    # 最小最適解のお題シノニムをお題セットに対応付ける
    theme_set_list = most_matched_synonym.head(1)["matched_theme_set"].values[0]
    matched_theme_sets = set(theme_set_list)  # 最小最適解が見つかったお題セットを格納
    for theme_set in theme_set_list:
        most_win_min[theme_set] = best_match_synonym

    # 最小最適解が見つかったお題セットを取り除いて、満たすお題セットを数え直す
    most_win_match_new = most_win_match.copy().drop("n", axis=1).apply(
        lambda r: remove_list_items(r["matched_theme_set"], matched_theme_sets), 
        result_type="expand", 
        axis=1
        )
    most_win_match_new.columns = ["n", "matched_theme_set"]
    return most_win_match_new[most_win_match_new["n"] > 0]

while True:
    most_win_match_list.append(extract_min_match(most_win_match_list[-1]))
    if len(most_win_match_list[-1]) == 0:
        break

多くのお題セットの最適解となれるお題シノニムを順番に選んだ結果は most_win_match_min.csv にまとめました。
お題シノニム theme_synonym_id、それが最適解となるお題セットの数 n、最適解となるお題セットのうち新規のお題セット matched_theme_set が記載されています。

また、お題セットごとに、選ばれた最多最適解を持つお題シノニムのリストは most_win_min.csv にまとめました。
お題セット theme_set_id、選ばれたお題シノニム theme_synonym_id、その中の町パターンの 1 つ pattern、お題シノニムの点数 1 - 26、このファイル内でのお題シノニムの登場回数 n_in_min が記載されています。

最多最適解のお題シノニム

最適解となれるお題セットが最多となるのは、得点が 1, 0, 1, 0, 4, 3, 2, 1, 5, 3, 3, 3, 1, 4, -3, 1, 2, 0, 1, 0, 7, 6, 1, 3, 3, 4 となるお題シノニムで、以下の 86 個のお題セットについて最適解となれます。

86 個
03_09_22, 03_09_26, 04_09_11, 04_09_14, 04_09_22, 04_09_25, 04_09_26, 04_10_15, 04_11_14, 04_11_22, 04_11_25, 04_11_26, 04_14_22, 04_14_25, 04_14_26, 04_22_25, 04_22_26, 04_25_26, 06_09_22, 06_09_26, 07_09_22, 07_09_26, 07_14_26, 08_09_11, 08_11_14, 09_10_11, 09_10_15, 09_10_26, 09_11_14, 09_11_16, 09_11_21, 09_11_22, 09_11_25, 09_11_26, 09_12_22, 09_12_26, 09_14_15, 09_14_22, 09_14_25, 09_14_26, 09_15_22, 09_15_26, 09_17_21, 09_17_22, 09_19_22, 09_19_26, 09_21_22, 09_21_26, 09_22_24, 09_22_25, 09_22_26, 09_23_26, 09_24_26, 09_25_26, 10_11_14, 10_11_15, 10_11_26, 11_14_16, 11_14_21, 11_14_22, 11_14_25, 11_14_26, 11_16_22, 11_21_22, 11_21_26, 11_22_25, 11_22_26, 11_25_26, 12_14_22, 12_14_26, 12_22_26, 12_25_26, 14_15_22, 14_15_26, 14_17_22, 14_19_22, 14_19_26, 14_22_24, 14_22_25, 14_22_26, 14_23_26, 14_24_26, 14_25_26, 22_24_26, 22_25_26, 24_25_26

2,600 全てのお題セットについての最適解の町の絵は、ナインタイルパニックの最適解を参照ください。

GitHubで編集を提案

Discussion