🔔

サンプルサイズの導出

2022/01/17に公開

統計

tech

はじめに

この記事では、サンプルサイズ設計、特に 2 標本の差の検定 で必要なサンプルサイズを計算する過程について記述します。勉強しながら筆者の理解したことを書いているので誤りもあるかもしれません。

計算の仮定

「新薬は既存薬より有効である」ことを、新薬治療群と既存薬治療群の 2 群における、ある検査値の平均値の差の検定で示したいとします。簡単のために、大きい方が治療が有効であるような検査値とします。

帰無仮説 $H_0$ ：既存薬群の平均値 $\mu_0\ge$ 新薬群の平均値 $\mu_1$
対立仮説 $H_1$ ： $\mu_0\lt\mu_1$

そもそもサンプルサイズを計算するモチベーションは、例数が多すぎても少なすぎてもよくないからです。

多すぎる場合は、時間・費用がかかる
少なすぎる場合は、実験が無駄になる可能性がある

そこで、そういった誤りを一定以下に抑えることができるであろう最小のサンプルサイズを計算します。以下のパラメータによって計算できます。

有意水準 $\alpha$ ：type I error の確率。小さい程嬉しい
検出力 $1-\beta$ ：真に有意であるときに正しく有意であると判断できる確率。1 から type II error の確率を引いた値。大きい程嬉しい
エフェクトサイズ $\Delta$ ：検出したい差。大きい程嬉しい
バラツキ $\sigma$ ：想定される個人差。小さい程嬉しい

計算の過程

対立仮説 $H_1$ は以下のように同値変形できます。

$H_1$
$\displaystyle\iff$ 既存薬群の平均値 $\displaystyle \overline{X_0}\sim\mathrm{N}\left(\mu_0, \frac{\sigma_0^2}{n_0}\right)$ と新薬群の平均値 $\displaystyle\overline{X_1}\sim\mathrm{N}\left(\mu_1, \frac{\sigma_1^2}{n_1}\right)$ が優位に離れている
$\displaystyle\iff \overline{X_0}-\overline{X_0}\sim f_0:\mathrm{N}\left(0, \frac{\sigma_0^2}{n_0}+\frac{\sigma_1^2}{n_1}\right)$ と $\displaystyle \overline{X_1}-\overline{X_0}\sim f_1:\mathrm{N}\left(\mu_1-\mu_0, \frac{\sigma_0^2}{n_0}+\frac{\sigma_1^2}{n_1}\right)$ が優位に離れている（ $\because$ 分散の加法性）

また、既存薬群と新薬群が等分散だと仮定し、被験者の割付を 1:1 とする場合、 $\sigma_0=\sigma_1$ , $n_0=n_1$ なので、今見たい分布は次の 2 つと見なせます。

$\displaystyle f_0:\mathrm{N}\left(0, \frac{2\sigma^2}{n}\right)$
$\displaystyle f_1:\mathrm{N}\left(\mu_1-\mu_0, \frac{2\sigma^2}{n}\right)$

この $f_0$ （赤）と $f_1$ （青）を描画したグラフが以下から見れます。数値を変更してグラフの変化も楽しめます。
https://www.geogebra.org/m/f6qdtau8
上のグラフでは $\alpha=0.05$ と固定していて、その値は橙の領域の面積と等しいです。また、水色領域の面積は、その $\alpha$ で帰無仮説 $H_0$ を棄却したときの type II error の確率 $\beta$ です。

次に、このグラフで各群の平均値間の距離を考えると、下で示すような2通りで表すことができます。
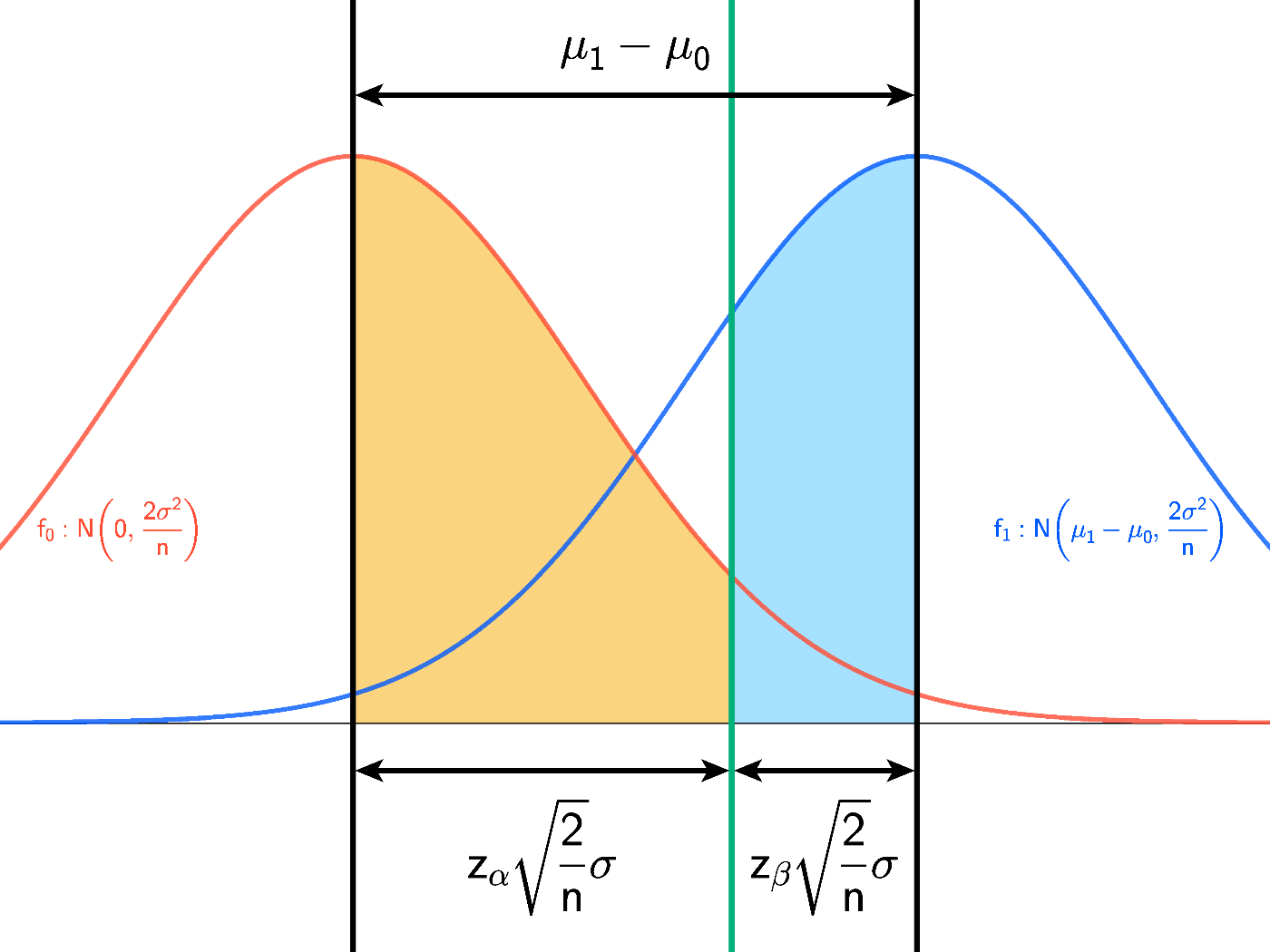
サンプルサイズ設計の図形的意味
これを等式で結ぶと、

\mu_1-\mu_0=z_\alpha\sqrt{\frac{2}{n}}\sigma+z_\beta\sqrt{\frac{2}{n}}\sigma \iff n=2\sigma^2\left(\frac{z_\alpha+z_\beta}{\mu_1-\mu_0}\right)^2

としてサンプルサイズを求めることができます。

※このグラフでは、わかりやすさのために、橙の面積 $=0.5-\alpha$ 、水色の面積 $=0.5-\beta$ 、としています。
また、両側検定 ( $H_0$ ： $\mu_0=\mu_1$ , $H_1$ ： $\mu_0\ne\mu_1$ ) の場合は、 $\alpha$ を $\displaystyle\frac{\alpha}{2}$ と置換すれば計算できます。

精度

上述の計算でサンプルサイズの概算はできますが、等分散性の過程、1:1 の割り付け、正規分布を用いてることなどから正確ではありません。

$f_0$ , $f_1$ の標準偏差： $s=\displaystyle\sqrt{\frac{\sigma_0^2}{n_0}+\frac{\sigma_1^2}{n_1}}$
$f_0$ , $f_1$ が従う t 分布の自由度： $\displaystyle\nu=\frac{\left(\sqrt{\frac{\sigma_0^2}{n_0}+\frac{\sigma_1^2}{n_1}}\right)^2}{\frac{\left(\frac{\sigma_0^2}{n_0}\right)^2}{n_0-1}+\frac{\left(\frac{\sigma_1^2}{n_1}\right)^2}{n_1-1}}$

このとき、以下の式を解いて算出したサンプルサイズ $n_0$ , $n_1$ が正確な値です。

\mu_1-\mu_0=z_\alpha(\nu)s+z_\beta(\nu)s

勉強中なこと

エフェクトサイズ（効果量）の設定
- 調べてると、 $\displaystyle\frac{\mu_1-\mu_0}{\sigma}$ なども出てきた
- Cohen の論文・書籍に記述がありそう
- Cohen, J. (1992). A power primer. Psychological Bulletin, 112(1), 155–159. https://doi.org/10.1037/0033-2909.112.1.155
- https://amzn.to/3e5nQqK （University of Toronto に PDF [9MB] が置いてある）
1 標本や対応のある 2 標本の場合のサンプルサイズ設計
Bayes 流の計算
分散未知で t 分布に従う場合の概算方法

\displaystyle n=\mathrm{SD}^2\left(\frac{z_\alpha+z_\beta}{\mu_1-\mu_0}\right)^2+\frac{z_\alpha^2}{2}

$\chi^2$ 検定や log-rank 検定などは一般化してこの式で求めれるそう

\displaystyle n=2\mathrm{SD}^2\left(\frac{z_\alpha+z_\beta}{\Delta}\right)^2

練習問題

ノルウェーにおいて、40 週の妊娠期間を満了して生まれた新生児の出生時体重の分布は近似的に正規分布になり、その平均は $\mu=3500$ グラム、標準偏差は $\sigma=430$ グラムである ^[1] 。妊娠期間中に喫煙していた女性から妊娠期間を満了して生まれた新生児の出生時の体重の平均は同じであるかどうかについての研究を計画する。もし喫煙していた女性から妊娠期間を満了して生まれた新生児の真の平均が $3200$ グラムと同程度に低い（あるいは $3800$ グラムと同程度に高い）とき、誤ってこの差を検出し損なう確率を $10\%$ にしたい。有意水準 $0.05$ の両側検定を実施するとする。この研究に必要とされるサンプルサイズはいくつか。

回答

この問題は「喫煙者から生まれた新生児の真の体重 $\overline{x}\ \mathrm{g}$ について、帰無仮説 $H_0$ : $\overline{x}=3500$ を有意水準 $\alpha=0.05$ で検定し、 $\overline{x}$ が $3200\ \mathrm{g}$ 以下（または $3800\ \mathrm{g}$ 以上）のときの検出力を $1-\beta=0.9$ 以上とできるサンプルサイズを算出する」ことと同義です。
すなわち、 $z_{\frac{\alpha}{2}}\approx1.96$ から、

\displaystyle \pm1.96=\frac{\overline{x}-3500}{\frac{430}{\sqrt{N}}} \longrightarrow \overline{x}\lt3500-1.96\cdot\frac{430}{\sqrt{N}}, 3500+1.96\cdot\frac{430}{\sqrt{N}}\lt\overline{x}

の範囲に $\overline{x}$ があるとき $H_0$ を棄却できます。
次に、 $z_\beta\approx1.28$ から、

\displaystyle \pm1.28=\frac{\overline{x}-3200}{\frac{430}{\sqrt{N}}} \longrightarrow \overline{x}\lt3200-1.28\cdot\frac{430}{\sqrt{N}}, 3200+1.28\cdot\frac{430}{\sqrt{N}}\lt\overline{x}

の範囲に $\overline{x}$ があるとき検出力を $0.9$ 以上に保てます。これらを等式に結ぶと、

3500-1.96\cdot\frac{430}{\sqrt{N}}=3200+1.28\cdot\frac{430}{\sqrt{N}} \iff N\approx21.57

より、喫煙していた女性から妊娠期間を満了して生まれた新生児 $22$ 人を対象に研究を行えばよいということになります。

参考文献

https://amzn.to/3e4hzeR
https://amzn.to/3IX4odO

脚注

A J Wilcox, and R SkjaervenEpidemiology Branch, National Institute of Environmental Health Sciences, Research Triangle Park, NC 27709. “Birth weight and perinatal mortality: the effect of gestational age.”, American Journal of Public Health 82, no. 3 (March 1, 1992): pp. 378-382. https://doi.org/10.2105/ajph.82.3.378 ↩︎