はじめに
この記事では、チェビシェフの不等式を導出する過程について記述します。勉強しながら筆者の理解したことを書いているので誤りもあるかもしれません。
さて、今年 2022 年実施の大学入学共通テスト(本試験)の数学 I・A の平均点が 40.25点と低いことで話題になりました 。また、大学入試センターは平均点だけでなく標準偏差も公開していて、今回のそれは 17.60点でした。
ここで、素直に点数が正規分布に従うと考えるとたとえば、1\sigma の範囲の [22.65, 57.85] に受験者の約 68% が、2\sigma の範囲の [5.05, 75.45] に受験者の約 95% がいると考えられます。しかし、正規分布を仮定できないような分布の可能性もあります。
そこで、どのような分布でも絶対的に成り立つ数式として、チェビシェフの不等式が存在します。
マルコフの不等式
チェビシェフの不等式の不等式を証明する過程でよく持ち出される「マルコフの不等式」という式が存在します。先人に倣って同様に導出します。
非負確率変数 X>0 について、その確率密度関数 f(x) を用いて期待値 \displaystyle E(X)=\int_{0}^{\infty}xf(x)dx の積分区間を定数 c で分けて考えると、
E(X)=\int_{0}^{\infty}xf(x)dx=\int_{0}^{c}xf(x)dx+\int_{c}^{\infty}xf(x)dx
となります。\displaystyle \int_{0}^{c}xf(x)dx\ge 0 から、
E(X)\ge\int_{c}^{\infty}xf(x)dx
と表せます。被積分関数の前半の x が全区間で c と縛ると、\displaystyle \int_{c}^{\infty}xf(x)dx\ge c\int_{c}^{\infty}f(x)dx から、
E(X)\ge c\int_{c}^{\infty}f(x)dx
とも表せます。ここで、定義から \displaystyle \int_{c}^{\infty}f(x)dx=P(X\ge c) なので、
と表せます。少し変形して \displaystyle P(X\ge c)\lt\frac{E(X)}{c} としてみると、これは「X がある数 c より大きい値である確率は、X の期待値を c で除した値より小さい」と言っていることになります。
チェビシェフの不等式
マルコフの不等式を用いれば、チェビシェフの不等式を導出するのは簡単です。上記のマルコフの不等式において、以下のように変数を置換します。
X\rightarrow\left|X-E(X)\right|^2, c\rightarrow(k\sigma)^2
このとき、\displaystyle E\left(|X-E(X)|^2\right) が X の分散であることも考慮して、
P\left(|X-E(X)|^2\geq(k\sigma)^2\right)\le\frac{E\left(|X-E(X)|^2\right)}{(k \sigma)^2}=\frac{\sigma^2}{k^2\sigma^2}=\frac{1}{k^2}
と変形することができます。不等式の P(\cdot) 内の 2 乗を外すと(\because\sigma\ge0)、
P\left(|X-E(X)|\geq k\sigma\right)\le\frac{1}{k^2}
となり、これが チェビシェフの不等式 です。
意味は「X の平均から、標準偏差の k 倍以上離れてる確率は、\displaystyle\frac{1}{k^2} 以下である」ということになります。
図で示すと、以下のようになります。
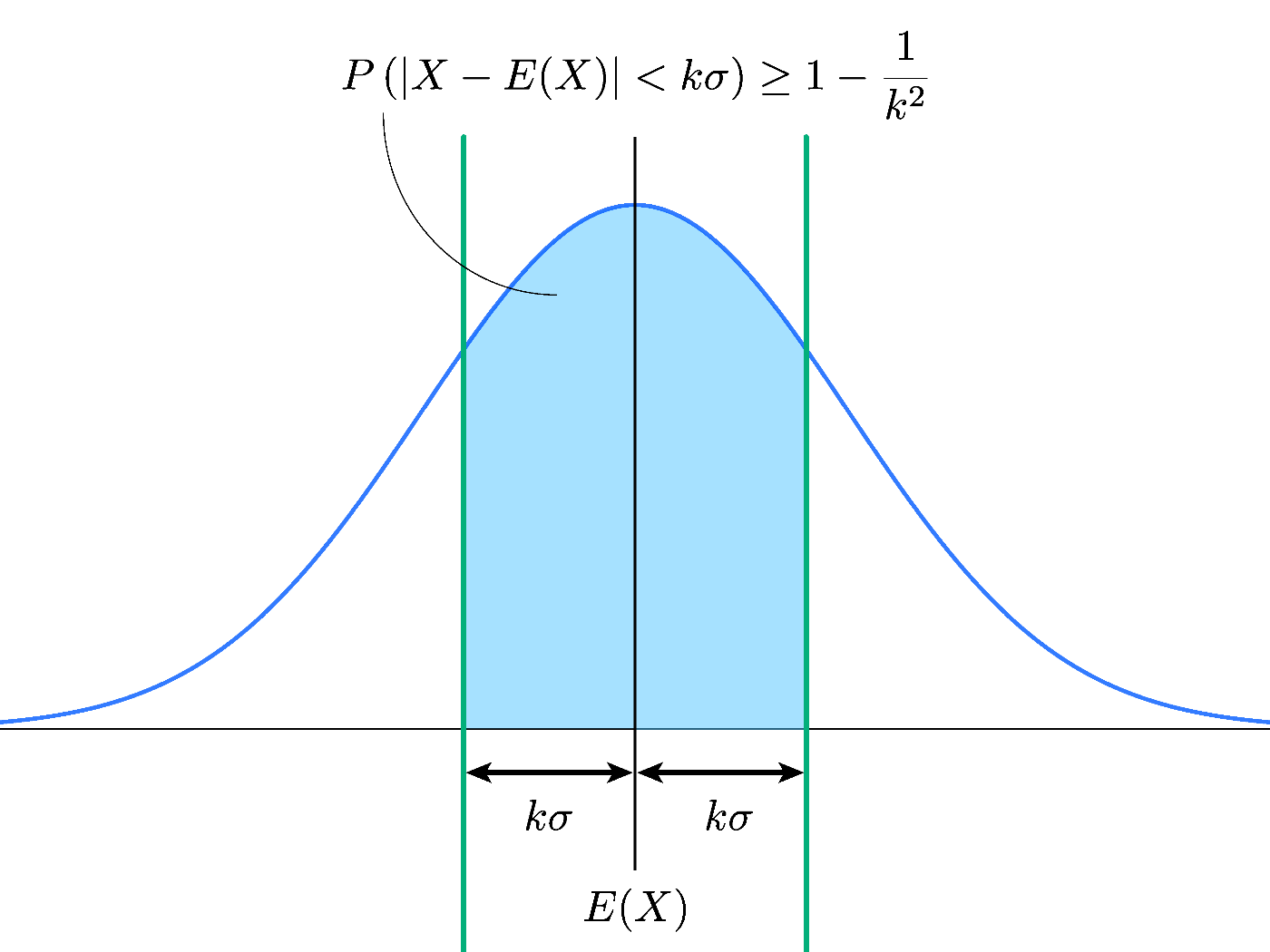
※正規分布で図を書いていますが、どんな分布でも成り立つ不等式です。また、導出した不等式の余事象について図示しています。
例えば、k=\sqrt{2} を代入すると、
P\left(|X-E(X)|\geq \sqrt{2}\sigma\right)\le\frac{1}{2}
なので、「期待値から標準偏差の \sqrt{2} 倍以上離れる確率は 50% 以下」ということが導け、これは分布に依らないことが分かります。
大数の弱法則
余談ですが、チェビシェフの不等式の最初の代入おいて、c\rightarrow k^2 とすると、
P\left(|X-E(X)|\geq k\right)\lt\frac{\sigma^2}{k^2}
となり、ここで確率変数として X の標本平均 \displaystyle \overline{X}=\frac{1}{N}(X_1+X_2+\dots+X_n) について考えると、E\left(\overline{X}\right)=E(X)、\displaystyle V\left(\overline{X}\right)=\frac{\sigma^2}{n} なので、
P\left(\left|\overline{X}-E(X)\right|\geq k\right)\lt\frac{\sigma^2}{k^2n}
となります。この式で n\rightarrow\infty と極限をとると、右辺が 0 になります。これは「サンプルサイズ n を大きくとると、標本平均と真の平均がある数 k 以上に離れている確率は 0 に収束する」ことを意味しています。このことを 大数の(弱)法則 と言います。
練習問題
冒頭の数学 I・A の点数分布に関して、平均点に近い方から 20% の人は最も広くて何点から何点の範囲にいるか。チェビシェフの不等式で示せる範囲で回答せよ。
回答
P\left(|X-E(X)|\lt k\sigma\right)=0.2 から、
0.2<1-\frac{1}{k^2}
\iff
k>\frac{\sqrt{5}}{2}
より、
40.25\pm\frac{\sqrt{5}}{2}\cdot 17.6
\iff
[20.57, 59.93]
の範囲に少なくとも 20% の受験者分布していることがわかります。
ちなみに、正規分布に従っている場合は、[35.85 ,44.65] の範囲が 20% なので、チェビシェフの不等式が保守的な式であることが分かります。
参考文献
https://amzn.to/3e4hzeR
https://amzn.to/3IX4odO

Discussion