📖
魚眼カメラに顔がどう映るか考える
魚眼カメラの映り方
有限会社フィットの記事を見ると、天球上の被写体が映像にどう映るかが分かります。
今回は等距離射影を考えます。カメラの中心軸と角度Θをなす方向にあるは点は中心からfΘの位置に投影されるようです。
実際のカメラ映像全体のシミュレーションは骨が折れるので、顔がどう映るかというテーマで簡単なシミュレーションを行います。
仮定
- 被写体は顔の画像で模擬します。すなわち顔がまったいらということにします。
- 魚眼カメラの画角は水平垂直方向ともに180°とします
3次元空間に顔の画像を配置したとします。画像上のあるピクセルの3次元的な位置がx,y,zで分かっているとし、下の図のような配置を考えます。
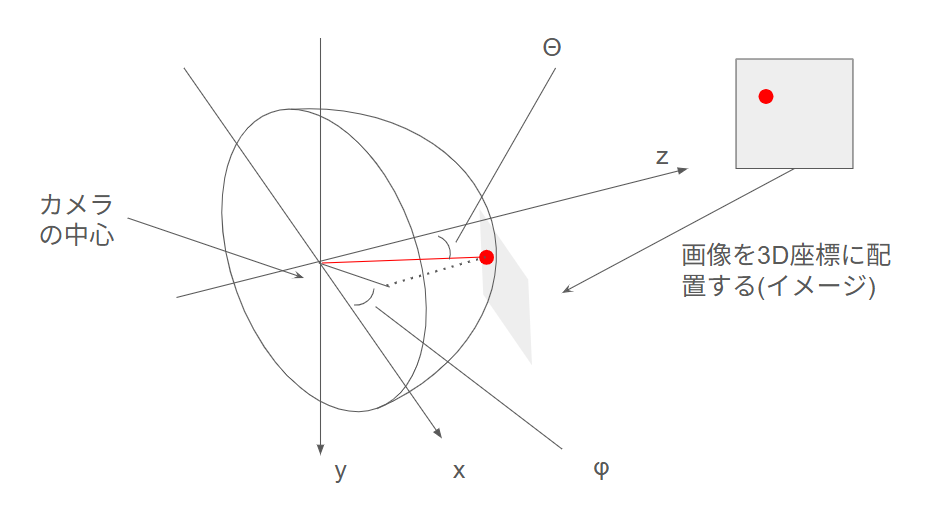
簡単のため、画像はxy平面い平行に配置して、yが負の方向に髪の毛がくるようにしています。
さて、画像上のある点(図中赤い点)のカメラに対する座標を(x,y,z)としたとき、角度は以下のように計算できそうです。
ここで
最初のレンズの解説をもとに対応する映像上の位置を求めると
ここで
これを対象の画像のすべてのピクセルについて計算すればよいので、下記のようなコードが出来上がります
実装
AIエディタにお願いして作った、html+js+cssのコードです。画像は置き換えたうえ、画像とカメラの距離を定義するポイント(画像上の一点)を指定してください。
<!DOCTYPE html>
<html lang="ja">
<head>
<meta charset="UTF-8">
<title>カメラシミュレーション</title>
<style>
body { font-family: sans-serif; }
.controls { margin-bottom: 1em; }
canvas { border: 1px solid #333; }
input[type=number] {
width: 180px;
font-size: 2.0em;
padding: 4px;
margin-right: 4px;
}
label {
margin-right: 8px;
font-size: 40px;
}
#select_image_label, #faceSelect, #updateBtn {
font-size: 40px;
}
</style>
</head>
<body>
<h1>カメラシミュレーション</h1>
<div class="controls">
<label id="select_image_label">顔画像:
<select id="faceSelect">
<option value="face1">顔1</option>
<option value="face2">顔2</option>
<option value="face3">顔3</option>
</select>
</label>
<label>x: <input type="number" id="inputX" value="100" step="1"></label>
<label>y: <input type="number" id="inputY" value="-100" step="1"></label>
<label>z: <input type="number" id="inputZ" value="600" step="1"></label>
<label>C: <input type="number" id="inputC" value="500" step="1"></label>
<label>α(°): <input type="number" id="inputAlpha" value="0" step="1"></label>
<label>β(°): <input type="number" id="inputBeta" value="0" step="1"></label>
<label>γ(°): <input type="number" id="inputGamma" value="0" step="1"></label>
<button id="updateBtn">更新</button>
</div>
<!-- <div style="width:800px; height:600px; overflow:auto; border:1px solid #333;"> -->
<canvas id="simCanvas" width="1000" height="1000"></canvas>
<!-- </div> -->
<script>
// 顔画像データ
const faceImages = {
face1: {
src: 'face1.jpg',
basePoint: {x: 50, y: 50} // 仮の基準点座標
},
face2: {
src: 'face2.jpg',
basePoint: {x: 50, y: 50} // 仮の基準点座標
},
face3: {
src: 'face3.jpg',
basePoint: {x: 50, y: 50} // 仮の基準点座標
}
};
const faceSelect = document.getElementById('faceSelect');
const inputX = document.getElementById('inputX');
const inputY = document.getElementById('inputY');
const inputZ = document.getElementById('inputZ');
const inputC = document.getElementById('inputC');
const inputAlpha = document.getElementById('inputAlpha');
const inputBeta = document.getElementById('inputBeta');
const inputGamma = document.getElementById('inputGamma');
const updateBtn = document.getElementById('updateBtn');
const canvas = document.getElementById('simCanvas');
const ctx = canvas.getContext('2d');
let faceImg = new Image();
// faceImg.setAttribute('crossOrigin', '');
let currentFace = 'face1';
function drawSimulation() {
ctx.clearRect(0, 0, canvas.width, canvas.height);
const face = faceImages[currentFace];
const x0 = parseFloat(inputX.value);
const y0 = parseFloat(inputY.value);
const z0 = parseFloat(inputZ.value);
const C = parseFloat(inputC.value);
const alphaDeg = parseFloat(inputAlpha.value);
const betaDeg = parseFloat(inputBeta.value);
const gammaDeg = parseFloat(inputGamma.value);
const alphaRad = alphaDeg * Math.PI / 180;
const betaRad = betaDeg * Math.PI / 180;
const gammaRad = gammaDeg * Math.PI / 180;
// 回転行列の成分
const cosA = Math.cos(alphaRad), sinA = Math.sin(alphaRad);
const cosB = Math.cos(betaRad), sinB = Math.sin(betaRad);
const cosG = Math.cos(gammaRad), sinG = Math.sin(gammaRad);
// 顔画像をcanvasに描画し、ピクセルデータを取得
const tempCanvas = document.createElement('canvas');
tempCanvas.width = faceImg.width;
tempCanvas.height = faceImg.height;
const tempCtx = tempCanvas.getContext('2d');
tempCtx.drawImage(faceImg, 0, 0);
const imgData = tempCtx.getImageData(0, 0, faceImg.width, faceImg.height);
// シミュレーションcanvasの中心
const cx = canvas.width / 2;
const cy = canvas.height / 2;
// x軸回転後の画像縦軸回転
let rod_xx = cosA + cosB*cosB*(1-cosA);
let rod_xy = -sinB*sinA;
let rod_xz = cosB*sinA;
let rod_yx = sinB*sinA;
let rod_yy = cosA + cosB*cosB*(1-cosA)
let rod_yz = cosB*sinB*(1-cosA)
let rod_zx = -1 * cosB*sinA;
let rod_zy = cosB*sinB*(1-cosA);
let rod_zz = cosA + sinB*sinB*(1-cosA);
// 顔画像の基準点を基準にカメラ座標系の原点を決める
for (let py = 0; py < faceImg.height; py++) {
for (let px = 0; px < faceImg.width; px++) {
const idx = (py * faceImg.width + px) * 4;
const r = imgData.data[idx];
const g = imgData.data[idx + 1];
const b = imgData.data[idx + 2];
const a = imgData.data[idx + 3];
if (a === 0) continue; // 透明は無視
// 顔画像の基準点をカメラ座標系の(x0, y0, z0)に合わせる
const dx = px - face.basePoint.x;
const dy = py - face.basePoint.y;
// 画像中心基準の座標に変換(画像サイズ64x64の中心は32,32)
const centerX = faceImg.width / 2;
const centerY = faceImg.height / 2;
const dx_center = px - centerX;
const dy_center = py - centerY;
// 画像中心基準でx軸回りβ回転
let x1 = dx_center;
let y1 = cosB * dy_center - sinB * 0;
let z1 = sinB * dy_center + cosB * 0;
// ロドリゲスの回転公式で画像を横に二つに割る軸で回転
let x2 = rod_xx * x1 + rod_xy * y1 + rod_xz * z1;
let y2 = rod_yx * x1 + rod_yy * y1 + rod_yz * z1;
let z2 = rod_zx * x1 + rod_zy * y1 + rod_zz * z1;
// 画像のbasePoint基準の座標系に戻す
let x3 = x2 + (centerX - face.basePoint.x);
let y3 = y2 + (centerY - face.basePoint.y);
let z3 = z2;
// カメラ座標系での位置に平行移動
let x4 = x0 + x3;
let y4 = y0 + y3;
let z4 = z0 + z3;
// カメラ座標系x軸回りγ回転
let x5 = x4;
let y5 = cosG * y4 - sinG * z4;
let z5 = sinG * y4 + cosG * z4;
// 魚眼投影
const r2 = Math.sqrt(x5 * x5 + y5 * y5);
const theta = Math.acos(z5 / Math.sqrt(x5 * x5 + y5 * y5 + z5 * z5));
const phi = Math.atan2(y5, x5);
const x_on_sim = C * theta * Math.cos(phi);
const y_on_sim = C * theta * Math.sin(phi);
// シミュレーションcanvas上の座標
const simX = Math.round(cx + x_on_sim);
const simY = Math.round(cy + y_on_sim);
if (simX >= 0 && simX < canvas.width && simY >= 0 && simY < canvas.height) {
ctx.fillStyle = `rgba(${r},${g},${b},${a / 255})`;
ctx.fillRect(simX, simY, 1, 1);
}
}
}
}
function updateFace() {
currentFace = faceSelect.value;
// faceImg.crossOrigin = "anonymous";
faceImg.src = faceImages[currentFace].src;
}
faceImg.onload = drawSimulation;
faceSelect.onchange = updateFace;
updateBtn.onclick = drawSimulation;
// 初期化
updateFace();
</script>
</body>
</html>
画像の位置や焦点距離由来の定数Cは可変とし、さらに画像を縦横軸回りに回転できるようにしています。(γはカメラの角度が違ったと起用に入れてみたものの蛇足な気がしている。)
※ローカルでの実行にはサーバが必要になる場合あり
Discussion