udemy講座メモ

⭐は引用が多すぎて結局書籍の内容を書き写してしまうことへの対策。⭐が多いほど重要なのではないか、という気持ちの表れ。

3 記述統計

分布とはどの値にどれくらいデータが存在するかを表したもの

ヒストグラム。連続変数の場合。sns.distplot(array, kde=bool)
棒グラフ。カテゴリ変数の場合。sns.catplot(x, data, kind='count')

記述統計
推測速統計

平均値の特徴
平均値は各値からの差の2乗の合計(平方和)を最小にする

偏差: 各データから平均を引く deviation
平均偏差: 偏差の絶対値の平均。偏差の平均の平方和は0。mean deviation

分散 np.var()
標準偏差 np.std()

4 2変数間の記述統計

共分散（covariance）

共分散行列（covariance matrix）
np.cov(xarray, yarray, bias=True)
bias=Trueがないと不変共分散行列を返すとのこと
np.cov(array, bias=True)

相関係数（correlatin cofficient）

共分散を標準化したのが相関係数。とりうる値（最小値 ~ 最大値）を-1 ~ +1の範囲にする

共分散の最大値

• 2変数が直線上にあるとき，正(負)の相関関係は最大
• それぞれの標準偏差をかけた値𝑠F𝑠Gが最大値になる

とのこと

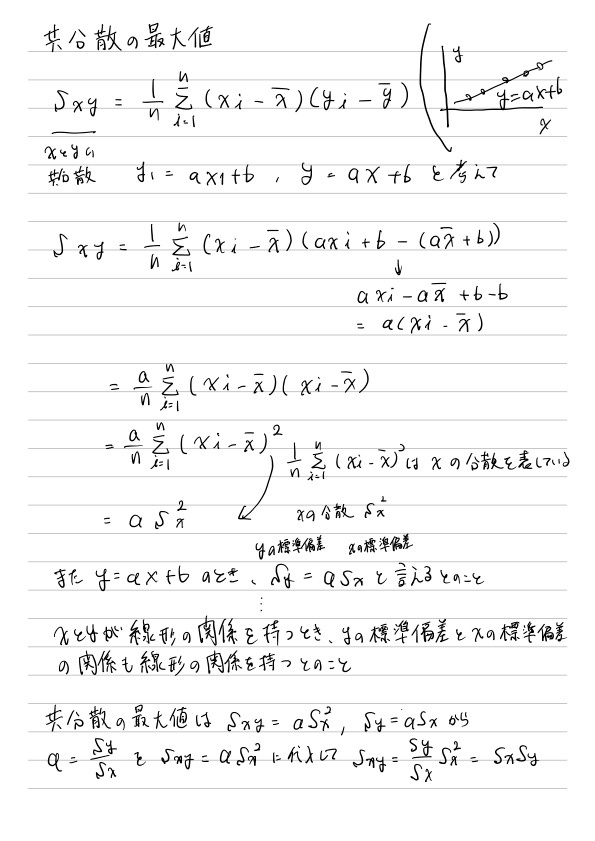
相関行列（correlation matrix）
np.corrcoef
df.corr()

相関行列の描画
sns.heatmap(df.corr())

連関（association）

カテゴリ変数の相関関係
分割表（contingency table）
観測度数（observed frequency）
期待度数（expected frequencies）

カイ二乗（χ²: chi squared）

観測度数が期待度数からどれくらい離れているかを計算した値

連関とカイ二乗の解説サイト

https://datawokagaku.com/chi2_test/

分割表を求める
pd.crosstrab
カイ二乗と期待度数を求める
stats.chi2_contingenecy
返り値の1つ目がカイ二乗、返り値の4つ目が期待度数の分割表

クラメールの連関係数

連関の強さを表す指標
カイ二乗（χ²）値を0~1に標準化した値

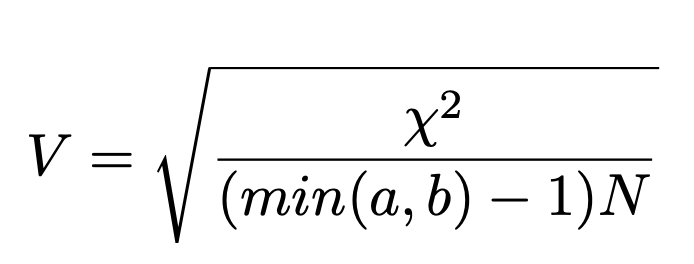
5 確率（probability）

確率変数（random variable）

確率分布（probability distribution）

stats.確率分布.メソッド

確率分布
norm（normal destribution、正規分布）
uniform
randint
binorm
poisson
expon

メソッド
rvs
pdf
cdf
sf
mean
var
std

とびとびの値をとる確率変数->離散型確率変数
連続の値をとる確率変数->連続型確率変数

サイコロを振って出た目
->離散型確率変数。関数fX(x)を確率質量関数（PMF: Probability Mass Functoin）

ランダムに選んだ成人男性一人の身長
->連続型確率変数。関数fX(x)を確率密度関数（PDF: Probability Density Function）

確率密度と確率

• 確率密度関数が描く面積が確率になる
• 確率密度関数が描く全面積は1になる

累積分布関数（CDF: Cumlative Distribution Function） PDFの積分結果を表す関数

stats.norm.pdf(x)
stats.norm.cdf(x)

確率密度関数の右側の面積を求める（1-累積分布関数）
stats.norm.sf(x)
Survival Function

カーネル密度推定（KDE: Kernel Density Estimation）
観測した分布から確率密度関数を推定する

KDEの確率分布を求める
stats.gaussian_kde(dataset)

KDEの描画
sns.displot(a, kde=True)
stats.gaussian_kde(dataset).plot

6 正規分布と標準化

標準化: 平均を0、分散を1にすること（z得点）

平均で引いて標準偏差で割る
この解説の中での標準偏差で割る部分が飛躍に聞こえていまいち納得できなかった。

標準正規分布（standard normal distribution）
平均0、分散1の正規分布（正規分布を標準化したもの）

参考: https://ai-trend.jp/basic-study/normal-distribution/normal-distribution/

sklearn.preprocessing.StandardScaler

scaled = StandardScaler().fit_transform(data)

二項分布（Binominal distribution）

ある事象が起こる確率𝑝の試行を𝑛回実施してその事象が𝑥回起こる確率(𝑃(𝑥))は

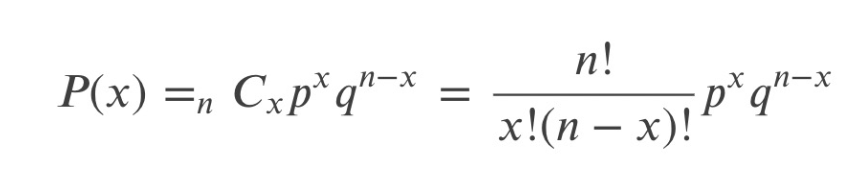
二項分布の確率分布を求める
stats.binom(n, p)

二項分布を描画する
stats.binom(n, p).pmf()

二項分布と正規分布
二項分布のnを無限大にした分布は正規分布に近似する

試行回数n、確率p、q=1-p
平均np、分散npqの正規分布に近似できる

7 推測統計入門

母集団

統計量
標本統計量

母集団の統計量を母数という

標本分布

標本の中身は確率的に変動。標本統計量も同様に確率的に変動する値。つまり確率変数。
標本平均のような標本統計量が従う確率分布を標本分布という。
-> 「ある標本の中の分布」 ではないことに注意（標本分布は理論上の分布）

不偏性（unbiasedness）

推定量が平均的に母数と一致する場合、その推定量は「不偏性がある」という
不偏性がある推定量を不偏推定量
確率の文脈では平均のことを期待値という

大量の標本をとって標本平均を計算したらそのほ標本平均は母平均に近づく
つまり、平均の標本分布の平均=母平均

平均の標本分布

平均の標本分布の平均は母平均と同じ𝜇になる
平均の標本分布の分散は母分散をnで割った値(\dfrac{σ²}{n})になる

不偏分散 （unbiased variance）

母分散の不偏推定量
不偏分散は，分散の式において𝑛ではなくて𝑛−1で割った値
通常の標本分散を𝑠²で表し，不偏分散を𝑠′²で表す

不偏分散の標本分布の平均値は母分散に一致する

n-1である解説

https://datawokagaku.com/unbiased_estimator/

イメージとしては、標本平均を使った分散はは母平均で計算した分散より過小評価されるので、その過小評価された分を\dfrac{n}{n-1}で補正する

不編分散の平方根

不偏分散の平方根は母集団の標準偏差𝜎の不偏推定量にはならない
不偏分散の平方根を「不偏標準偏差」と呼ぶのは間違い

Pythonで不偏分散

不偏分散を求める
stats.tvar
np.var(a, ddof=1)
delta degree of freedom（degree of freedom: 自由度）1を指定すると不偏分散を求めるようになる、とのこと

不偏分散の平方根を求める（不編標準偏差ではない）
stats.tstd
np.std(a, ddof=1)

まとめ

⭐⭐

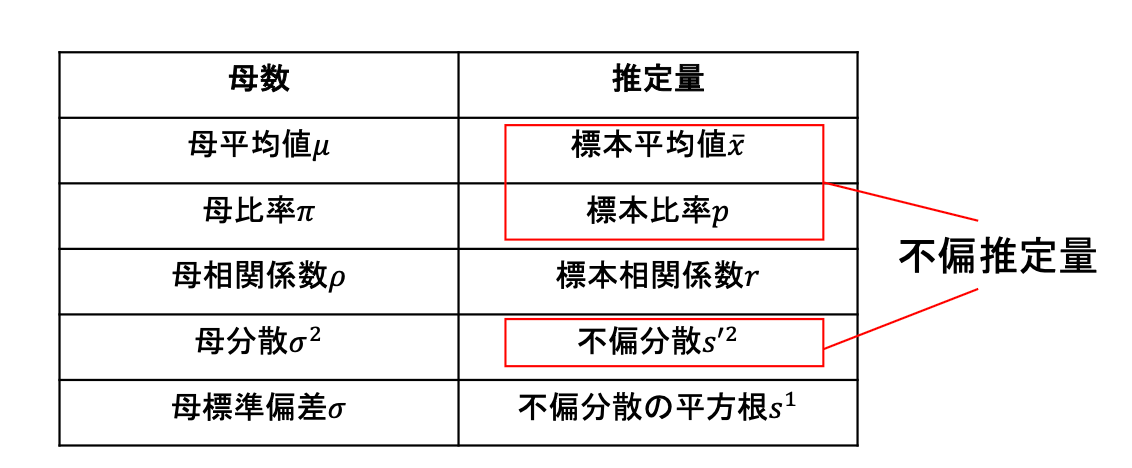
講座資料より抜粋

8 区間推定

信頼区間（CI: Confidence Interval）

比率の標本分布

比率の標本分布は二項分布から考えることができる
二項分布「ある観察や試行を複数回行った時に，ある事象が起こる 回数が従う確率分布」Chapter6参照

参考

https://www.youtube.com/watch?v=LrGP3H93dFM

https://toketarou.com/binomial/

比率の区間推定

比率の標本分布、標本比率がどれくらいの確率で得られるかを考えるには、標準化して標準正規分布で考える必要がある

比率の区間推定

⭐⭐

Pythonで比率の区間推定

比率の区間推定をする
stats.binom.interval(alpha, n, p)

平均値の区間推定

t分布

平均𝑥¯の標本分布において，母集団の標準偏差𝜎の代わりに標本標準偏差𝑠′を用いた場合の標準化後の平均𝑥¯が従う確率分布

引用: https://datawokagaku.com/t_dist/

stats.t(degred of freedom).pdf()

9 統計的仮説検定とは

10 2郡の比率差の検定（z検定）

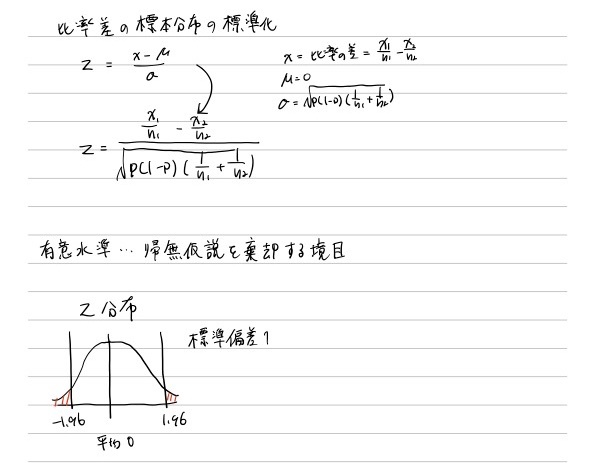
p値: 帰無仮説が正しいとしたときにその検定統計量が得られる確率をp値という

対応表がある値だと思う。

11 連関の検定（カイ二乗検定）

連関の検定（カイ二乗検定）

2つのカテゴリー変数間に連関があるかを検定する
帰無仮説には「連関がない(=独立)」
対立仮説には「連関がある(=独立ではない)」

p値: 帰無仮説が正しいとしたときにその検定統計量が得られる確率をp値という
また、帰無仮説が正しいとしたときに標本から計算されたカイ二乗値𝜒²が得られる確率

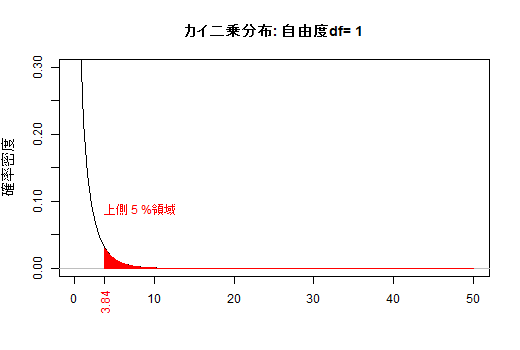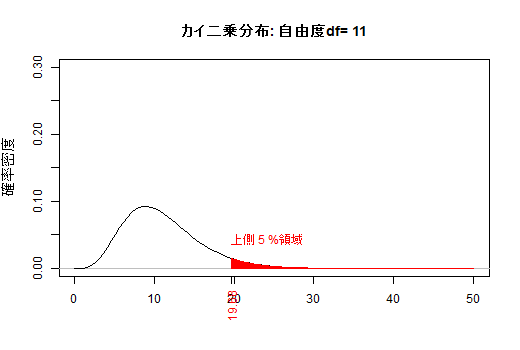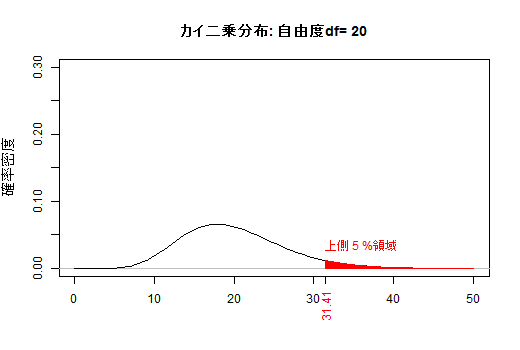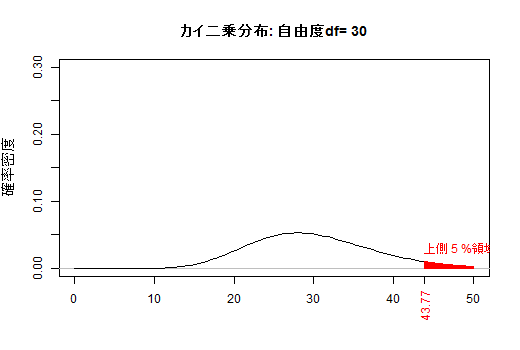
引用: お茶の水女子大(とのこと。Google画像検索より。サイト訪問しても画像がなかった)

横軸 カイ二乗値𝜒²。それより右側の面積がp値

縦軸

確率密度というのは、たとえば横軸3のところで切った右側の面積が「カイ２乗値が3以上になる確率」になるように決めたものです。

(よく分からないなぁ。「右側の面積が」の部分いるの？カイ二乗値が3と面積が3になるのは関係ないような)

引用: https://kogolab.chillout.jp/elearn/hamburger/chap3/sec2.html

標本から計算した 𝜒² が棄却域に入るかをみる

標本からを𝜒²を計算して，𝜒²分布でどれくらいの確率で得られるかを計算する
棄却域に入らなければ2つの変数に連関があるとは言えない
棄却域に入れば2つの変数に連関がある(独立ではない)と言える

python 連関の検定（カイ二乗検定）

chi2, p, dof, ex = stats.chi2_contingency(obs, correction=False)
obs: 観測度数
correction: イェイツの修正

イェイツの修正（yates's correction）

カイ二乗値を小さくする修正を加えた式。p値が高くなる。
このモチベーションはもともとのカイ二乗分布からのp値を算出する中でズレがあるからとのこと。しかし用途は限定的とのこと。

カイ二乗検定とZ検定

比率差の検定は、自由度1のカイ二乗検定で代替できるとのこと。

帰無仮説は、連関なし = 比率差なし
対立仮説は、連関あり = 比率差あり

カイ二乗検定とZ検定（比率差の検定）

Z検定
proportions_ztest([x1が起こった回数, x2が起こった回数], [サンプル数n1, サンプル数n2], alternative='two-sided')

カイ二乗検定
stats.chi2_contigency([連関表の1行目, 連関表の2行目], correction=False)

12 2群の平均値差の検定（t検定）

平均値差の検定とは（対応なしと対応あり）

対応なしは、被験者が全く異なる母集団A、Bに、投薬なし（A）、投薬あり（B）の実験を与えて、その結果の平均に差があるかを検定する、とのこと
対応ありは、被験者が同じ母集団Aに投薬前と後での結果の平均に差があるかを検定する、とのこと。

平均値差の検定のパターン

平均の標本分布

大標本の場合の平均値差の標本分布と・平均値差の標本分布の標準化

2つの母集団に共通な分散の推定値

𝜎²の推定値

t検定

スチューデントのt検定 stats.ttest_ind(a, b, equal_var=True)
ウェルチのt検定: stats.ttest_ind(a, b, equal_var=False)

13 正規性と等分散性の検定

シャピローウィルクの検定とは

帰無仮説: 母集団が正規分布に従う（観測分布と正規分布に"差がない"）
対立仮説: 母集団が正規分布に従わない

今までの検定とは違い、「帰無仮説を棄却したくない」。
しかし、帰無仮説を棄却できなかったからと言って、帰無仮説を積極的に肯定、採択することはしない
-> 「正規分布に従う」という仮説を否定できなかった、に留めておく。
まとめると、シャピローウィルクの検定は、任意の標本が正規分布から得られたものだという仮説を否定できなかった、に留まるものになる。

とはいえ、帰無仮説を棄却できなかった、というだけでも効果がある、とのこと。

Q-Qプロット

Quantile: 分位数

シャピローウィルク検定する時に使用するもの

理屈はよく分からなかった。@TODO 別の資料で調べる

statsmodels.api.qqplot(data, line='r')
line='r'で、regression（回帰）の結果を描画する

シャピロ-ウィルク検定はQ-Qプロットにおいて，どれくらい直線からずれているかを検定する

Python シャピローウィルク検定

stats.shapiro(x)
データxに正規性があるかを検定する
第一戻り値は検定統計量
第二戻り値はp値

等分散性の検定 F検定とは

帰無仮説: 分散に差がない
対立仮説: 分散に差がある

ここは、シャピローウィルク検定のように棄却させたくない、といったことはなく、いままでどおり棄却させて対立仮説に持っていくことを目指す

分散の比率の標本分布（F分布）を考える

分散の比率で差がないと考えて棄却域な値が算出されれば対立仮説に持っていける。

F分布

stats.f(dfn, dfd)

dfn: 分子の自由度
dfd: 分母の自由度

stats.f(dfn, dfd).pdf(x)

F検定

p値を調べて差がないと棄却されるか、されないかを調べて、等分散性があるか、ないかを調べる。

差がない（-> 棄却されない） -> 等分散性がある
差がある （-> 棄却された） -> 等分散性がない

まとめ

検定の前に検定を行うことは正しくないという指摘もある（検定の多重性）

例えば、F検定したあとに、ウェルチのt検定か、スチューデントのt検定かを選択することは必ずしなければいけないことではない。

ウェルチのt検定がフォールバック的なメソッドとして扱われる。

14 対応ありの平均値差の検定とは

標準化することでz分布で考えることが可能
母標準偏差 𝜎-は未知なので，標本の変化量の不偏分散の平方根𝑠′-を推定量として使用⇨t分布

Python 対応ありの平均値差の検定とは

stats.ttest_rel(a, b)
a, bはデータのarray
第一戻り値は検定統計量t
第二戻り値はp値

検定の誤りと検定力

第1種の誤り
第2種の誤り

第1種の誤りを起こすα

あわてて誤りを起こすαと覚えるとよいとのこと

間違えて棄却してしまった。もし有意水準が5%だったら間違いを起こす確率αは5%。

第2種の誤りを起こすβ

棄却できなかった。対立仮説に持っていけなかった。

αとβのトレードオフ

αとβはトレードオフの関係にある

検定力

どれだけ正しく帰無仮説を棄却し対立仮説を成立できるか

検定力に影響を与える3つの要素

1. 有意水準
2. サンプルサイズ
3. 帰無分布と対立分布の差（効果量）

有意水準は5%か1%を使う。固定。
サンプルサイズだけが変化できる。サンプルサイズが大きければ大きいほどいいわけではない。

検定料と効果量

⭐

16 検定力分析（power analysis）

検定力分析とは

1. 検定の結果としてp値だけでなく効果量も合わせて報告する
   ⇨既に標本が手元にあって，それを検定に使うケース
2. 想定する効果量に基づいて適切なサンプルサイズを算出する
   ⇨これから標本抽出から始めるケース(検定のデザイン)

Cohen's d

Python 検定力分析

有意水準，効果量，検定力，サンプルサイズを残りの値から算出する

t = statsmodels.stats.power.TTestIndPoswer
t.solve_power(effect_size, nobs1, alpha, power, raRo, alternaRve)

⭐

検定力の推移を描画

t = statsmodels.stats.power.TTestIndPoswer
t..plot_power(dep_var, nobs, effect_size, alpha)