冠動脈の血行動態モデル

末端樹木モデルに基づいたヘッドロスありの0Dモデル

(A patient-specific lumped-parameter model of coronary circulation / Zheng Duanmu)

モデル化

冠動脈全体の類似回路網を図7 に示す。 この回路網では、冠動脈のすべての端末が、構造化樹木モデルから計算されたルート・インピーダンスに割り当てられている。Pietrabissaらによる研究7 と同様に、このネットワークには心血管系の閉ループモデルが含まれています。心筋内圧（RVPG および LVPG 時）は圧力発生器として機能し、心臓内の冠動脈の位置に応じて、心室内圧の 3 分の 1 または半分に選ばれる26。冠動脈はモデル内でシミュレートされ、同時に右心房にリンクされる。また、全身循環と肺循環も含まれている。右心室圧発生装置（RVPG）と左心室圧発生装置（LVPG）はフィードバック項である。左冠状静脈（LCV）と右冠状静脈（RCV）もターミナルインピーダンス（Z）としてシステムに接続される。

冠動脈樹は閉ループの循環器系で表現し、R hは 頭部損失による変動抵抗、Z1～Z10は冠動脈血管の末端に取り付けた構造化樹モデルのルートインピーダンスである。

集中定数モデルの数理

血液をニュートン流体とし、血管を円筒管とする。各血管内の流れの支配方程式は

$$-{\rm{\Delta }}p=L\frac{\partial q}{\partial t}+Rq$$

$$q=C\frac{\partial p}{\partial t}$$

ここで、pは圧力、Δp は圧力損失、qは流量である。その他のパラメータは、水力抵抗R、各血管の弾性容量C、血流の慣性Lである。したがって、回路における抵抗、静電容量、インダクタンスに類似して、以下のようになる

$$R=\frac{128\mu l}{\pi {D}^{4}},\quad C=\frac{\pi {D}^{3}l}{4Gh},\quad L=\frac{4\rho l}{\pi {D}^{2}},$$

ここで，μは血液粘度，ρは密度，Gは血管のヤング率，lはセグメント長，Dは直径，hは血管の肉厚である．CTデータから推定した全血管のパラメータを表1に示す。心拍数は75回/分（心周期0.8秒）で計測した。また、

$$μ = 4 × 10^{−3} kg · m^{−1}s^{−1}, ρ = 1.04 × 10^{3} kg/m^{3} , G = 2 × 10^{5}Pa$$

とし、Dを血管径として壁厚hは 0.08D とした

CTデータから推定された患者別冠動脈モデルのパラメータ

血液は心室から供給されるため、左心室（LV）と右心室（RV）のポンプ機能を以下のように選択した。

$${P}_{v}=\{\begin{array}{ll}{U}_{0}\sigma (t)+E(V-{V}_{0})+{R}_{v}\dot{V} & {\rm{systole}}\\ {E}_{d}(V-{V}_{0}) & {\rm{diastole}}\end{array}$$

ここで、P v は心室圧、U0は体積V0でのピーク等体積圧、Eは時間変化するエラスタンス、活性化関数σ(t) = [1 -cos(2πt/t s) ]である。t s は収縮期、Vは基準容積、𝑉 ˙ V˙ は容積変化率、 R v は心室心筋の抵抗、E d はパッシブエラスタンスである。

血管分岐部でのインピーダンスは

$$\frac{1}{{Z}_{p}}=\frac{1}{{Z}_{d1}}+\frac{1}{{Z}_{d2}}\mathrm{.}$$

N世代からなる対称木の端子インピーダンスは

$$Z=\frac{8\mu \lambda }{\pi {r}_{0}^{3}}\frac{2{\alpha }^{3}-{(\frac{1}{2\alpha })}^{N}}{2{\alpha }^{3}-1},$$

動脈漸減指数率を2.76としたときの娘血管rd、親血管rpの比α=rd/rp = 0.778
r0は元のルート半径
λ = 50は小動脈の長さと半径の比を定義する定数

ヘッドロスの評価

血管構造に伴うエネルギー損失と損失係数は、ベルヌーイの式に組み込むことができる9。図8に示すような冠動脈の入口部におけるヘッドロス（断面積変化による急激な圧力損失）をモデル化するために、圧力損失を次のように推定する。

$${\rm{\Delta }}p=\frac{\xi \rho {v}^{2}}{2}$$

ξは局所抵抗であり，血管狭窄径比 0.5，Re=100 の場合，Festerらの経験式 ξ=288/Re から 2.88 と推定され，vは平均流速である．そして、ヘッドロスによる抵抗R hは

$${R}_{h}=\frac{{\rm{\Delta }}p}{q}=\frac{\xi \rho }{2{A}^{2}}q\mathrm{.}$$

上記を計算すると、冠動脈の半径r(mm)を用いて、

$$R_{h} [mmHg・ms/ml] = \frac{1.14q}{r^{4}}$$

左右の冠動脈樹のヘッドロスの位置と、断面積の狭窄によるヘッドロスの位置。

冠動脈の1Dモデル

A One-Dimensional Hemodynamic Model of the Coronary Arterial Tree (Zheng Duanmu1)

冠動脈末端のモデリング

べき乗則

各末端大動脈の遠位端は，心筋内にある小血管の血管床（モデルでは構造化ツリーで表現）に接続されている．構造化木では、半径rpの親血管は半径rd1=αrpとrd2=βrpの2本の子血管に分岐する（0<β<α<1）。分岐過程は以下。ξは半径指数、ηは面積比、γは非対称比。ξ = 2.76

1D冠動脈のモデリング

連続の式と運動量方程式

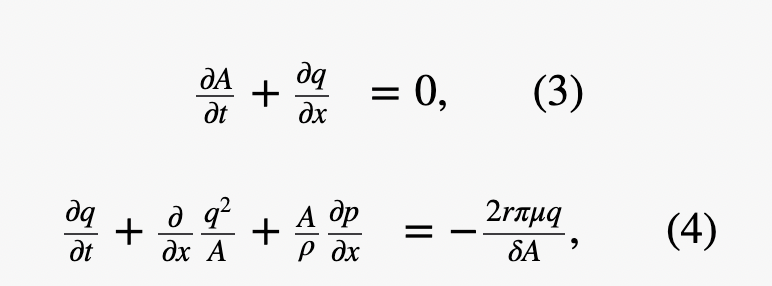
血管の流体力学

Numerical Simulation and Experimental Validation of Blood Flow in Arteries with Structured-Tree Outflow Conditions, OLUFSEN

大血管における流体力学

血管の典型的な流体力学的モデリングの仮定は以下

• 不透過性
• 軸対称
• 弾性円筒
• 非圧縮性(密度ρは一定)
• ニュートン流体(粘性μは一定)
• 流体の圧力P(x,t)は面積に依存しない(rに依存しない)
• 血管は指数関数的に先細りになる
• 血管は半径方向のみに動き、軸方向には動かない
• 血管内膜に接する場所での軸方向速度は0

$$u=[u_{r}(r,x,t) ,u_{x}(r,x,t)]$$

$$rは半径方向の座標、xは血管に沿った位置座標 \\ tは時間，u_{r}は半径方向速度，u_{x}は軸方向速度$$

$$断面積 A(x,t) = \pi R(x,t)^{2} \\ r_{0}(x) = r_{t}exp(log(r_{b}/r_{t})x/L) \\ L: 血管の長さ, r_{t}：入り口の半径, r_{b}:出口の半径 \\$$

連続の式

$$\frac{\partial u_{x}}{\partial x} + \frac{1}{r} \frac{\partial (ru_{r})}{\partial r} = 0$$

上記を断面積で積分して、

$$2\pi\int_{R}^{0} (\frac{\partial u_{x}}{\partial x} + \frac{1}{r} \frac{\partial (ru_{r})}{\partial r}) rdr = 0$$

以上より、断面積Aと流量qを用いて、

$$\frac{\partial q(x,t)}{\partial x} + \frac{\partial A(x,t)}{\partial t} = 0$$

運動量保存

$$\frac{\partial u_{x}}{\partial t} + u_{x}\frac{\partial u_{x}}{\partial x} +u_{r}\frac{\partial u_{x}}{\partial r} = -\frac{1}{ρ}\frac{\partial P}{\partial x} + \frac{\nu}{r}\frac{\partial}{\partial r}(r\frac{\partial u_{x}}{\partial r}) \\ 動粘性\nu = \frac{\mu}{ρ}$$

$$\nu\frac{\partial^2 u_{x}}{\partial x^2}は無視する (<< \frac{\nu}{r}\frac{\partial}{\partial r}(r\frac{\partial u_{x}}{\partial r})のため)$$

連続の式を使い変形を進めると

$$\frac{\partial q}{\partial t} + \frac{\partial}{\partial x}(2\pi\int_{0}^{R}u^2_{x}rdr) + \frac{A}{ρ}\frac{\partial P}{\partial x} = 2\pi\nu[r\frac{\partial u_{x}}{\partial r}]^R_{0}$$

境界層近似を行い、下記のような流速曲面を仮定する

$$u_{x}(x,r,t)= \left\{ \begin{array}{ll} \bar{u_{x}}(x,t) & (r<R-\delta) \\ \bar{u_{x}}(x,t)(R-r)/\delta & (R-\delta < r < R) \end{array} \right.$$

$$\delta \approx (\nu/\omega)^{1/2} \approx 0.09cm \\ \nu = 0.046 cm^{2}/s$$

上記を用いて計算すると、

$$2\pi\int_{0}^{R}u_{x}^{2}rdr = \frac{q^{2}}{A}(1+\frac{2\delta}{3R}+\mathcal{O}(\delta^{2}))$$

$$2\pi\nu[r\frac{\partial u_{x}}{\partial r}]^R_{0} = -\frac{2R\pi\nu}{\delta}\frac{q}{A}(1+\mathcal{O}(\delta))$$

以上より一次元の運動方程式は

$$\frac{\partial q}{\partial t} + \frac{\partial}{\partial x}(\frac{q^{2}}{A})+\frac{A}{ρ}\frac{\partial P}{\partial x} = -\frac{2R\pi\nu}{\delta}\frac{q}{A}$$

これは解析的に解けないため、2段階Lax–Wendroff法を用いた数値計算を行う。

保存則形式にする

また、下記のようにBを導入すると、

$$B(r_{0}(x),p(x,t)) = \frac{1}{\rho} \int_{p_{0}}^{p(x,t)}A[r_{0}(x),p']dp'$$

$$\frac{\partial B}{\partial x} = \frac{A}{\rho} \frac{\partial p}{\partial x} + \frac{\partial B}{\partial r_{0}}\frac{dr_{0}}{dx}$$

以上より下記の保存則形式を得る。

$$\frac{\partial q}{\partial t} + \frac{\partial}{\partial x}(\frac{q^{2}}{A}+ B) = -\frac{2R\pi\nu}{\delta}\frac{q}{A} + \frac{\partial B}{\partial r_{0}}\frac{dr_{0}}{dx}$$

血管内壁条件・ラプラスの法則

$$p - p_{0} = \frac{4}{3}\frac{Eh}{r_{0}}(1-\sqrt{\frac{A_{0}}{A}})$$

ここで、$r_{0}$は血管半径、hは壁厚、$p_{0}$は基準圧力、$A_{0}$は $p＝p_{0}$のときの断面積、Eはヤング率で、以下のように$r_{0}$の関数として与えられる。

$$\frac{Eh}{r_{0}} = k_{1}e^{k_{2}r_{0}} + k_{3}$$

小血管

分岐部境界条件

質量保存

$$q_{pa} =q_{d1}+q_{d2}$$

エネルギー保存

ベルヌーイの定理。エネルギー損失は親速度の2乗に比例(比例定数K)
速度はすべて平均速度

$$p_{d1}=p_{pa}+\frac{\rho}{2}((u_{pa})^{2}-(u_{di})^{2}) - \frac{K_{di}\rho}{2}((u_{pa})^{2})$$

ただし、細動脈では下記の式のように圧保存で近似できる。

$$p_{pa} = p_{di}$$

流出路境界条件

小動脈は二元的かつ非対称的に構造化された木の集合体。
そのような木はそれぞれ、細動脈のレベルに達するまでの世代数が可変。
なぜなら、そのレベルが大動脈と細動脈をつなぐ小動脈では、粘性効果が大動脈よりも重要であり、慣性効果はそれに比例して小さくなる。大動脈と細動脈をつなぐ小動脈では、粘性効果が大動脈よりも重要であり、慣性効果はそれに比例して小さくなる。従って、非線形項は削除し、粘性効果をより詳細にモデル化する。

また、各血管を直線として扱うことである。特に、小動脈の各樹木の根元のインピーダンスを再帰的な数値手順で計算することができる。これらのルートインピーダンスは、大動脈の流出境界条件となる

小血管での流体力学方程式

大血管のナビエ・ストークス方程式と比較して、慣性項が粘性項より小さいため、これを無視すると、

$$\frac{\partial u_{x}}{\partial t} + \frac{1}{ρ}\frac{\partial P}{\partial x} = \frac{\nu}{r}\frac{\partial}{\partial r}(r\frac{\partial u_{x}}{\partial r}) \\$$

各種パラメータ

In vivo Coronary flow

(https://journals.physiology.org/doi/full/10.1152/ajpheart.00603.2013 より)
収縮早期（S1）、収縮後期（S2）、拡張早期（D1）、拡張後期（D2）

冠動脈狭窄のモデル化

α = AS/A0
A0: 正常断面積, AS: 狭窄した面積

$${R}_{s}={R}_{0}{\alpha }^{-2}\quad {C}_{s}={C}_{0}{\alpha }^{\mathrm{3/2}}\quad {L}_{s}={L}_{0}{\alpha }^{-1}$$

α = 100 − p, p: 面積減少率

PDAの狭窄の程度が異なる場合の圧力（左）と流量（右）。

$$\,{\rm{FFR}}\,=\frac{{p}_{d}}{{p}_{a}}\mathrm{.}$$

$$p_{d} : 遠位部の圧力$$

$$p_{a} : 近位部の圧力$$

(a)冠動脈の狭窄とFFRの典型的な表示。(b)シミュレーションのPDA対狭窄部、Pijls & Bruyneによる測定との比較、(c)無次元流体シミュレーション対狭窄部、Matesらによる測定との比較.

冠動脈の0Dモデルでどのように患者データから推定するか

冠動脈の長さと冠動脈体積のスケーリング関係を使う方法

Estimation of the flow resistances exerted in coronary arteries using a vessel length-based method(Kyung Eun Lee)

心筋の血管の構造と密度が似ていることから，すべての抵抗がほぼ同じであり，共通の値（R 1 = R 2= ...= R n）で 表されると仮定する

$$R=R_{1} / n$$

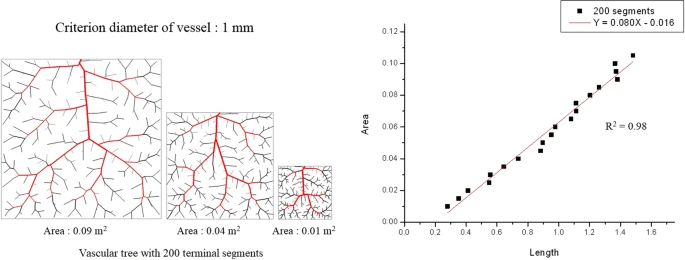
ここで、nは娘血管の分岐密度に直接関係する。図1に示すように、娘血管は母血管に沿ってほぼ一様に分布しているため、娘血管の数nは母血管の長さlに比例する

$$R = R_{1} k / n$$

LV体積はRV体積の3.46倍であるという臨床観察

様々な面積（0.09 m2, 0.04 m2, 0.01 m2など）で最適化した血管フラクタル木のモデリング（左図）と、面積（体積）と血管の全長との直線関係（右図）。

参考文献

1. Analysis of lumped parameter models for blood flow simulations and their relation with 1D models
   血管網の0次元モデルが1次元の線形システムの1次離散化と見なすことができることを証明
2. Mathematical analysis of the quasilinear effects in a hyperbolic model blood flow through compliant axi-symmetric vessels
   Navier-Stokes方程式の軸対称形式の特性を詳細に研究している。血管の半径が特性波長に対して小さい場合、半径方向の運動量方程式は、圧力がどの断面でも一定であることを示し、血管の断面積で軸方向に運動量方程式を積分すると、半径方向の速度項は面積項に包含されることを実証した。この仮定は実用的な血管の流れに対して有効であるため、結果として得られる1次元モデルは、流れ、圧力、面積を基本変数として定式化することの妥当性を与える
3. Review of Zero-D and 1-D Models of Blood Flow in the Cardiovascular System
   包括的なレビュー