Zenn
Open27

機械学習に再入門するのでメモ

Python
機械学習
みぎみぎ

副業データアナリストが機械学習に再入門するときのメモ

みぎみぎ

Udemy【実践】ビジネスケースとつなげてPythonで出来ること5つを学べる3日間集中コース

まずは流れと実装を確認したかった。手を動かす前にざっくり1.5H動画を流し見た。
https://www.udemy.com/course/python-can/

コンテンツ

  • Pythonでデータ加工・集計・描画
  • Pythonで機械学習モデル構築
  • PythonでWebスクレイピング
  • PythonでAPI利用
  • PythonでWebアプリケーション開発

学び

  • Seabornの図綺麗。もっと意識的にSeabornを使っていこうと思った。
  • とりあえず初手LightGBM
  • 前処理もある程度固まってきたら関数化していく時の具体例
    • 人のコード読むの勉強になる（今更）
  • SeleniumやFlaskのざっくりとした使い方がわかった
みぎみぎ

書籍「Pythonではじめる機械学習」

なんだかんだと体型的にまとめられていて相当良い。ザクっと体型的に振り返れた。
https://www.amazon.co.jp/Pythonではじめる機械学習-―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎-Andreas-C-Muller/dp/4873117984

みぎみぎ

k-NN（k最近傍法）

訓練データセットの中から一番近い点から多数決（投票）でクラス分類するアルゴリズム。n_neighbor=xの引数で近傍の何点で多数決するかを決める。※回帰モデルもあるけど無視

  • 1つの最近傍点のみを用いると、決定境界は訓練データに近くなる（汎化性が低い）
  • データセットの複雑さにもよるが、n_neighborsごとにtrainデータとtestデータのAccuracyを比較すると最良の（もしくはおそらくこの辺で問題ない）最近傍点の数が明らになる。
# load and split dataset
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# k-nn instance
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)

# クラス分類期の訓練（学習）
clf.fit(X_train, y_train)

# 予測
print('Test set predictions: {}'.format(clf.predict(X_test)))

# モデルの汎化性評価
print('Test set accuracy: {:.2f}'.format(clf.score(X_test, y_test)))
みぎみぎ

回帰

線形回帰（最小二乗法）

  • 学習データにおいて、予測と真値yとの平均二乗誤差(MSE)が最小になるようなパラメータを求める。
  • 線形回帰には傾きと切片以外のパラメータがなく、これは単純で良いとも言えるし、モデルの複雑さを制御する術がないとも言える。
    • 訓練データの次元が低い場合は、モデルがとても単純なので過学習の恐れがない。一方で高次元データになると、複雑な問題に汎化性をもって対応できず、過学習が起こりやすくなる。
    • 入力データが2次元程度であれば線形回帰は有効な場合があるだろう。そうでなければ、もっと複雑度を制御できるモデルを探す必要がある。
  • データ数が少ない時、線形回帰はほとんど汎化性能を獲得することができない。

Ridge回帰

  • 直感的には、予測をうまく行いつつ、個々の特徴量の出力に与える影響をなるべく小さくしたい。
  • 過学習を防ぐために明示的にモデルを制約することを正則化という。
    • Ridge回帰ではL2正則化と呼ばれる。
  • 十分な学習データがある場合にはRidge回帰と線形回帰は同じ性能を示す。

Lasso回帰

  • Ridge回帰と違いL1正則化を使っている。
  • まずはRidge回帰を使ってみればよい。しかし、特徴量がたくさんあって、そのうち重要なものはわずかしかないことが予測されるなら、Lassoの方が向いている。
みぎみぎ

クラス分類

  • 線形クラス分類器には、ロジスティック回帰、線形サポートベクターマシン（SVM）がある。

    • パラメータCで正則化の強さを決めており、Cが大きくなるほど正則化が弱まる（過学習しやすくなる）
    • 基本的に線形クラス分類は2クラス分類に適用するものである。

  • 線形モデルの訓練は非常に高速で、予測も高速である。非常に大きいデータセットにも適用できるし、疎なデータセットに対してもうまく機能する。

  • 線形モデルの利点の一つはモデルが数式的にわかりやすいこと。一方で、各係数がなぜその値になったのかはわかりにくい（解釈性は低い）

みぎみぎ

木系モデル

決定木

  • 決定木は構造上過学習しやすい。過学習を防ぐために
    • 事前枝刈り：モデルの構築過程で木の生成を早めに止める
    • 事後枝刈り：一度木を構築してから情報量の少ないノードを削除する
  • sklearnのDicisionTreeRegressorとDecisionTreeClassifierクラスに実装されている。

木の可視化

treeモジュールのexport_graphvizで可視化できる。

feature inportance | 特徴量の重要度

DecisionTreeClassifier(random_state=0).future_importances_で出せる。

特徴

  • 結果が容易に可視化可能で、専門家出なくても解釈可能であること
  • データのスケールに対して完全に不変であること
みぎみぎ

アンサンブル法

  • 複数の機械学習モデルを組み合わせることで、より強力なモデルを構築する方法
  • 回帰でもクラス分類でも、ランダムフォレストが現在最も多く使われている機械学習手法。非常に強力である上、多くの場合はそれほどパラメータチューニングせずに使えてかつ、データのスケールを気にする必要がない。
  • 主要なパラメータは決定木の数を指定するn_estimatorsと個々の木がそれまでの決定木の誤りを補正する度合いを制御する学習率learning_rate、そして個々の決定木の複雑さを減らすmax_depthである。
    • ランダムフォレストの場合はn_estimatorが大きければ大きいほどよかったが、勾配ブースティングの場合には複雑なモデルを許容することになり、過学習を招く（バギングとブースティングの違い）
    • n_estimatorsを時間とメモリ量で決めておいて、learning_rateに対して探索を行う方法がよく用いられる。
    • 勾配ブースティングでは、max_depthは非常に小さく設定される。深さが5以上になることはあまりないい。
  • 勾配ブースティングとランダムフォレストは同じようなデータを得意とするので、一般的にはランダムフォレストを先に試した方がいい。こちらの方が頑強だからだ。ランダムフォレストがうまく行ったとしても、予測時間が非常に重要な場合や、機械学習モデルから最後の1%まで性能を絞り出したい場合には勾配ブースティングを試してみると良いだろう。
  • 主な短所は、パラメータチューニングに細心の注意が必要なこと、訓練にかかる時間が長いこと。また、高次元の疎なデータにはうまく機能しない。

ランダムフォレスト（RF）

  • 決定木の最大の問題点は学習データに過学習してしまうこと。RFはこの解決策である。
  • RFは要は少しずつ異なる決定木をたくさん集めたもの
  • ランダムにたくさんの木を作る
    • 1/ 決定木を作るためのデータポイントを選択する際に乱数を利用する方法
    • 2/ 分枝テストに用いる特徴量を選ぶ際に乱数を利用する方法
  • ブートストラップサンプリング
    • 決定木が少しずつ違うデータセットに対して構築されるようになる方法
    • n_samples個のデータポイントから、交換有りでデータポイントをランダムにn_samples回選び出す手法のこと（つまり、復元抽出）
    • 木の個々のノードが異なる特徴量のサブセットを使って決定を行うようになる
  • ランダムフォレストは本質的にはランダムであり、乱数のシードを変更すると構築されるモデルが大きく変わる可能性がある。結果を再現可能にしたいのであれば、random_state=を固定する必要がある。

勾配ブースティング木（Gradient Boosting Decision Tree：GBDT）

  • 回帰にもクラス分類にも使用できる
  • RFとは対照的に、勾配ブースティング木では、1つ前の決定木の誤りを次の決定木が修正するようにして、決定木を順番に作っていく。デフォルトでは乱数性はない。その代わり、強力な事前枝刈りが用いられる。
  • 勾配ブースティングでは、深さ1~5くらいの浅い決定木が作られる。これによって、モデルに占めるメモリが小さくなり、予測も早くなる。
    • ポイントは弱学習機を多数組み合わせることにある。
from sklearn.ensemble import GradientBoostingClassifier

<参考>
バギングとブースティングの違いがわかりやすい。feature_importanceの話もある。
https://upura.hatenablog.com/entry/2018/05/26/214453

（追記）
XGBoost、LightGBM、CatBoostの違い
https://logmi.jp/tech/articles/322734

Level WiseとLeaf Wise
https://qiita.com/kuroitu/items/57425380546f7b9ed91c

みぎみぎ

サポートベクターマシン（SVM）

特徴

  • 様々なデータセットに対してうまく機能する強力なモデル
    • 非線形の要素を持ち込むことで超平面での分類を可能にする
  • SVMを用いると、データにわずかな特徴量しかない場合にも複雑な決定境界を生成することができる。
  • 低次元のデータでも高次元のデータでも（つまり特徴量が少なくても多くても）うまく機能するが、サンプルの個数が大きくなるとうまく機能しない。
    • 10,000サンプルくらいまではうまく機能するが、100,000サンプルぐらいになると、実行時間やメモリ使用料の面で難しくなってくる。

問題点

  • 注意深くデータの前処理とパラメータ調整をする必要があること
    • 勾配ブースティングが人気な理由もこの点がeasyだからである
  • ある予測がされた理由を理解することが難しく、モデルを専門家以外に説明することが大変
みぎみぎ

ニューラルネットワーク(ディープラーニング)

ニューラルネットワーク、ディープラーニングﾁｮｯﾄﾜｶﾙ

長所

  • 最大の利点は、大量のデータに含まれているデータを費やし、信じられないほど複雑なモデルを構築できること。十分な時間とデータをかけて、慎重にパラメータを調整すれば、他の機械学習アルゴリズムに勝てることが多い（クラス分類でも回帰タスクでも）。

欠点

  • 複雑なモデルが作れることの裏返しで、訓練に時間がかかる。さらに、データを慎重に前処理する必要がある。SVMと同様にデータが「同質」な場合、つまり全ての特徴量が同じ意味を持つ場合に最もよく機能する。（そうでない場合はスケールを揃えたり、重みをつけたりする必要がある）
    • 様々な種類の特徴量を持つデータに関しては、決定木に基づくモデルの方が性能が良いだろう。
  • ニューラルネットワークのパラメータチューニングはそれ自体が一つの技芸になっている。
  • 結果の可視化がしにくく、解釈がしにくい課題がある。

<補足>
この書籍が詳しいので、入門するならこちらがおすすめ。
NN ~ DL/CNNくらいまではカバーしてる
https://www.amazon.co.jp/dp/4873117585/ref=cm_sw_em_r_mt_dp_W70ZF26NPYQFHVXZN0EP

みぎみぎ

教師なし学習

概要

  • データセットの変換とクラスタリング
    • 最も一般的なデータセットの変換は次元削除。そのほかにも文章からトピックを抽出するなど
    • クラスタリングアルゴリズムは、データを似たような要素から構成されるグループに分けるアルゴリズム。

教師なし学習の難しさ

  • アルゴリズムが学習したことの有用性の評価が難しい（アルゴリズムが「よくやった」のかどうかを判断するのは難しい）
  • そのため、教師なし学習は、大きな自動システムの一部として利用される場合よりも、データよりよく理解するために、探索的に用いられることが多い。もしくは、教師あり学習の前処理としての特徴量エンジニアリングに使われる。
みぎみぎ

データ変換

まあ、いろんな手法があるよってことで

  • SrandardScalor : ここの特徴量の平均が0, 分散が1になるように変換する
  • MinMaxScalor : データがちょうど0から1の間にはいるように変換する
  • Normalizer : ここのデータポイントをユークリッド長1になるように変換する。言い換えると、データポイントを半径1の円（より高次元なら超球面）に投射する。
みぎみぎ

次元削除、特徴抽出、多様体学習

  • 次元削除：PCA
  • 多様体学習 : t-SNE

この辺りは割愛

みぎみぎ

クラスタリング

k-meansクラスタリング

  • k-meansクラスタリングは最も単純で最も広く用いられているクラスタリングアルゴリズム
    • データのある領域を代表するようなクラスタ重心を見つけようとする。
    • 2つのステップを繰り返す。(1)ここのデータポイントを最寄りのクラスタ重心に割り当てる、(2)ここのクラスタ重心をその点に割り当てられたデータポイントの平均に設定する。データポイントの割り当てが変化しなくなったら、アルゴリズムは終了する。

skleanで簡単にkmeansモデルが作れる

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

# 合成２次元データを作る
X, y = make_blobs(random_state=1)

# クラスタリングモデルを作る
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)

print('Cluster membership:\n{}'.format(kmeans.labels_))

# 新しいデータセットに対する予測もできる
print(kmeans.predict(X))

k-meansがうまくいかない場合

  • 仮に、データセットに対する正しいクラスタ数がわかっていたとしても、k-meansがそれをうまく見つけられるとは限らない。（それぞれのクラスタは重心で定義されているため）
  • 例えば、下のようなデータの分布については直感とは異なる話kれ方をしているように見える。本来なら半円弧ごとにクラスタになってほしい気持ちがある。

<参考>
このページでは、実際にK-meansをブラウザで体感できる。動作原理のイメージがつきやすい。
http://tech.nitoyon.com/ja/blog/2013/11/07/k-means/

みぎみぎ

4章 特徴量エンジニアリング

  • 連続値特徴量とカテゴリ特徴量（離散値特徴量）
  • 特定のモデルに対して、最良のデータ表現を探索することを特徴量エンジニアリングと呼ぶ。データサイエンティストや機械学習実践者の主な仕事の1つである。
    • 教師あり学習では、データを正しく表現することは、パラメータを適切に選ぶことよりも、大きな影響を与えることもある。

one-hot-encoding（ダミー変数化）

  • Pnadasもしくはscikit-learnで変換可能

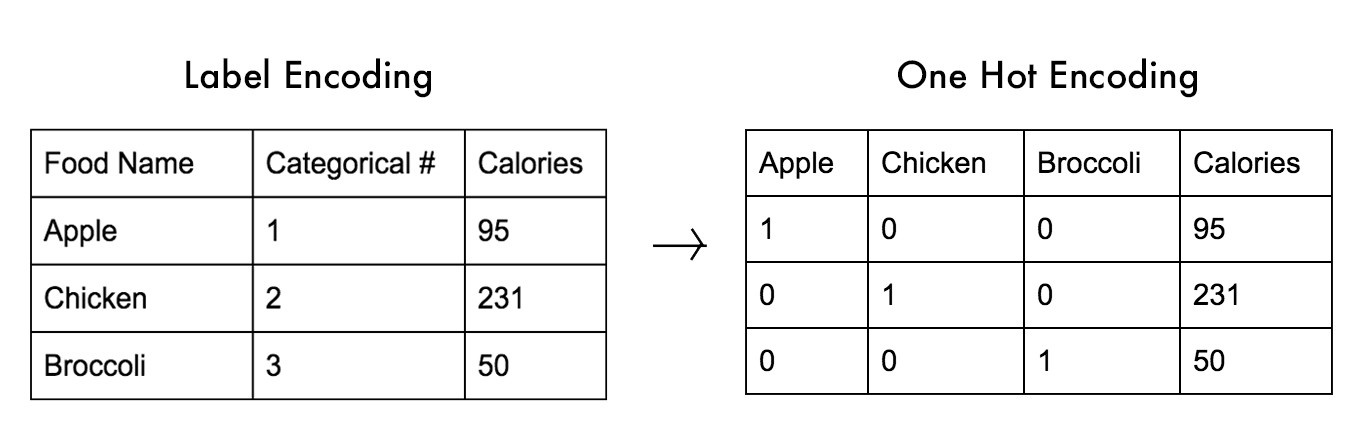
カテゴリ文字列特徴量を整数特徴量にする

  • DataFrame.map()でよくやる手法

ビニング、離散化

  • 年齢を年代に分ける処理がわかりやすい

モデルベース特徴選択

  • 教師あり学習モデルを用いて個々の特徴量の重要性を判断し、重要なものだけを残す手法。
    • 決定木や決定木ベースのモデルのfeature_importance_など

専門家知識の活用

  • 要はドメイン知識
  • ドメインの専門家が、最初に得られるデータ表現よりもはるかに情報量の多い有用な特徴量を特定する手助けをしてくれることは多い。

この辺りは「特徴量エンジニアリング」や「Kaggle本」をみる方が知見が得られそう。

みぎみぎ

モデルの評価と改良

  • データを学習データとテストデータに分割するのは、新しく見たことのないデータに対するモデルの汎化性能を計測するためであることを思い出そう。学習データに対する適合度には興味がなく、訓練中には見ていないデータセットに対する予測の精度を見たいのだ。

交差検証（k-hold cross-validation）

  • ただ学習データとテストデータを分割する方法と比べて、より安定で徹底した手法。
  • 交差検証では、データの分割を何度も繰り返して行い、複数のモデルを訓練する。最もよく使われるのはk分割交差検証
    • 多くの場合 k = 5~10。
    • 交差検証の制度をまとめるには、一般には平均値を用いる

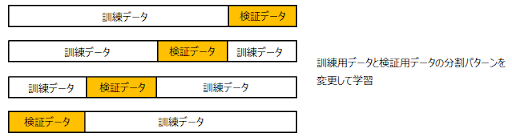
scikit-learnで簡単に実装できる。

from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

iris = load_iris()
logreg = LogisticRegression()

# cross_val_score はデフォルトで3分割交差検証を行い、3つの精度を返す
scores = cross_val_score(logreg, iris.data, iris.target, cv=3)
print('Cross validation scores:{}'.format(scores))

# k=5
scores = cross_val_score(logreg, iris.data, iris.target, cv=5)
print('Cross validation scores:{}'.format(scores))

# 平均値を用いる
# このモデルは平均で97%の割合で正しいと結論づけられる。
print('Average cross-validation score:{:.2f}'.format(scores.mean()))

交差検証の利点

  • 交差検証を使えば（train_test_splitのようにランダムなデータセット作りではなく）、全てのデータ正確に1度だけテストに用いられる。個々のデータはいずれかの分割に属しており、ここの分割は一度だけテストに用いるからだ。従って、モデルはデータセットのすべてのサンプルに対して良い汎化性のを示さなければ、交差検証のスコアとその平均を高くすることはできない。
  • データを多数に分割すると、モデルの敏感さをみることができる。例えば、精度が90~100%の間で変動したとすると（これはかなり大きな変動だが）、このモデルが最悪の場合と最良の場合でどの程度の性能を示すかがわかる。
  • train_test_splitに比べて、効率的にデータを使うことができる。
    • train_test_splitを用いると、通常75％のデータを学習に用い、25％を評価に用いる。
    • 5分割交差検証であれば、それぞれの回で4/5(80%)のデータを学習に用いる。10分割交差検証であれば9/10(90%)を学習に用いる。データが多ければ多いほど、モデルは正確になる。
  • なお、交差検証の最大の問題は計算コストである。k個のモデルを学習させるため、単純な分割の場合に比べておよそk倍遅くなる。

層化k分割交差検証（StratifiedKFold）

  • いつもk分割交差検証がうまくいくとも限らない。例えば、[0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1…]というデータセットがあった場合には、前半と後半でデータの特性が明らかに異なっているからだ。
    • 無作為抽出によるk分割交差検証の方法もあるが、ランダム性がある限り解消されない可能性がある。
  • そういう場合に使う分割方法で、層化k分割交差検証がある。層化抽出法を使うと、サブセットを作るときに目的変数の比率がなるべく元のままになるように分割できる。一般に、クラス分類器（モデル）を評価するには層化k分割交差検証を使った方が良い。こちらの方がより信頼できる汎化性能の推定ができるからだ。

<参考>
https://blog.amedama.jp/entry/2018/08/25/174530

グリッドサーチ

  • パラメータをチューニングしてモデルの汎化性能を向上させる方法。
  • 基本的にはパラメータの全ての組み合わせに対して試してみる方法
みぎみぎ

評価基準とスコア

  • 機械学習モデルの評価基準を選ぶ前に、そのモデルよりも抽象度の方レベルで目的を考える必要がある。これはしばしばビジネス評価基準と呼ばれる。
  • 機械学習アプリケーションに対して特定のアルゴリズムを選択した結果はビジネスインパクトと呼ばれる。抽象度の高い目的とは、例えば交通事故を防ぐとか病院への入院回数を減らすと言ったようなことだ。

2クラス分類の基準

  • 陽性・陰性・偽陽性・偽陰性

    • 混同行例（confusion_matrix）、精度（Accuracy）、F-score、適合率（Precison）、再現率（Recall）

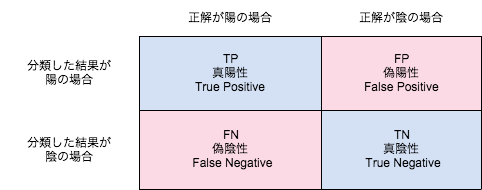
    • RecallとPrecisionはトレードオフの関係だよって図。閾値によってどのクラスに分類されるかは変わる。確率分布だから。

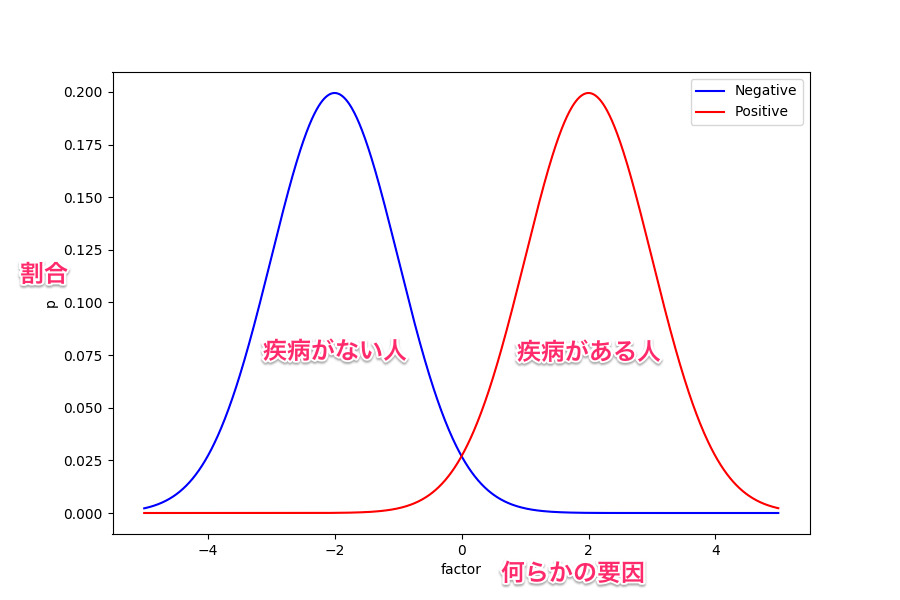
<参考>
昔よくお世話になった図。これが一番わかりやすい。
https://zellij.hatenablog.com/entry/20120214/p1

  • 偏ったデータセット
  • 適合率-再現率カーブ（PR曲線）とROCカーブ
    • モデルがクラス分類の判断を行う閾値を変更することで、クラス分類器の適合率と再現率のトレードオフを調整することができる。あるクラスに対して、特定の再現率や適合率が決められたら、それに応じて閾値を決めることができる。
      • 例えば、再現率90%を満たす閾値を設定することは常に可能。難しいのはこのような閾値でも適切な適合率を保てるようなモデルを開発することだ。全て陽性だと判断すれば再現率を100%になるが、そんなモデルには意味がない。
    • 適合率と再現率の「ちょうど良い塩梅」を探すのに役立つのがPR曲線。2つの指標の組み合わせを同時に見ることができる。
    • PR曲線はscikit-learnを使って確認することができる（実装例は別途調べる）。
from sklearn.metrics import precision_recall_curve

みぎみぎ

ROC曲線とAUC

  • クラス分類器の解析に使われる指標の1つ。PR曲線との違いは、再現率と適合率の代わりに、偽陽性率と新陽性率（再現率）をつかう。
from sklearn.metrics import roc_curve
  • ROC曲線においては、理想的な点は左上に近い点。つまり、低い偽陽性率を保ちながら高い再現率を達成するのは理想。

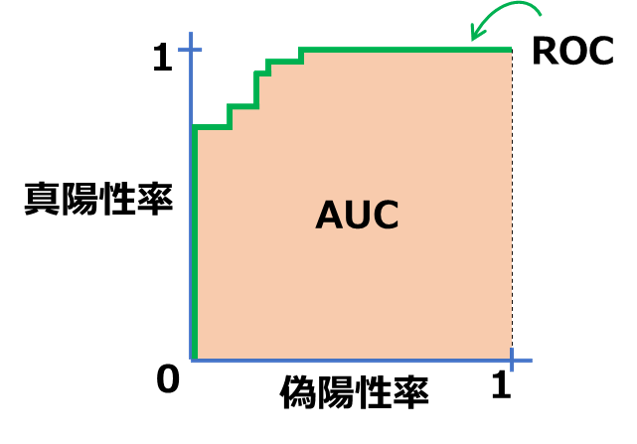
<参考>
AUCとは「左上の近くを通る」を表した指標。最高がAUC=1.0、最悪がAUC=0、ランダムに予測するとAUC=0.5
https://www.cresco.co.jp/blog/entry/15337/

Confusion_Matrixがあるとわかりやすい
https://www.sairablog.com/article/machine-learning-roc-auc.html

みぎみぎ

おわりに

  • 「もし完全なモデルができたとしたらどうなるか？」を考えてみよう。不正なトランザクションを完全に検出できたとして、会社が月に100ドルしか節約できないのなら、アルゴリズム開発を始めるべきですらない。一方で、月に数万ドル節約できるのなら、問題を解析する価値がある。
  • モデルを試す際には、それが大きなデータサイエンスワークフローの一部であることを忘れてはいけない。
  • 品源をループに組み込む。機械学習モデルには「単純な問題」を判断させ、比較的少ない「複雑な場合のみ」人間に任せれば良い。
  • 運用システムには、使い捨ての解析スクリプトとは異なる性質が要求されることを覚えておこう。

この本の次にどこへいくのか

  • 理論を学ぶ
    • 統計学、確率論、線形代数、最適化といったアルゴリズムの背景にある理論を学ぶ
  • 他の機械学習フレームワークとパッケージを使ってみる
    • Pythonならstatsmodel、C++ならvowpal wabbitなど
  • ランキング、推薦システム、その他の学習
  • 確率モデル、推論、確率プログラミング
  • ニューラルネットワーク
  • 大規模データセットへのスケール
    • アウトオブコア学習とクラスタ並列か
  • 名誉を得る
    • エキスパートになるには練習を繰り返すしかない

結論（相当良いので原文ママです）

機械学習が幅広いアプリケーションに対しても有効で、実際に実践するのも簡単だ、ということを理解してもらえたことと思う。今後もデータ解析を続けてほしい。ただし、問題の全体像を見ることを忘れずに。