はじめに
しばらく前に大学受験を終えたluna_moonlightです。突然ですが、数学に苦しめられたという経験はありますか?おそらく多くの方は数学、特に受験数学に苦しめられたことがあるでしょう。そんな数学の問題にも、プログラミングを使えば一瞬にして答えがわかってしまうようなものがあります。この記事では、受験数学をプログラミングで倒してみなさんの無念を晴らす(?)とともに、そのプログラムの高速化の方法について解説していきます。
一橋大学 2020年 大問1(1)
10^{10}を2020で割った余りを求めよ。
数学解法
解法
\begin{split}
&10^1 \equiv 10 \pmod {2020}\\
&10^2 \equiv 100 \pmod {2020}\\
&10^3 \equiv 1000 \pmod {2020}\\
&10^4 \equiv 10000 \equiv 1920 \pmod {2020}\\
&10^5 \equiv 10^4 \cdot 10 \equiv 1920 \cdot 10 \equiv 19200 \equiv 1020 \pmod {2020}\\
&10^6 \equiv 10^5 \cdot 10 \equiv 1020 \cdot 10 \equiv 10200 \equiv 100 \pmod {2020}\\
\end{split}
周期性より、10^{10} \equiv 100 \pmod {2020}
プログラミング解法
愚直
愚直に10を10回かけて、2020で割った余りを求めます。
a = 10
b = 10
mod = 2020
ans = 1
for _ in range(b):
ans *= a
ans %= mod
print(ans)
この方法だと、指数の肩をNとしてO(N)で答えが求まります。
高速化
x^{2N}=x^N \cdot x^Nなので、この計算を繰り返し用いることで、指数の肩が2の冪乗の場合は高速に計算できます。なので、指数の肩を2の冪乗に分解することで高速に計算できます。分解方法は、2進数表記への変換と対応しています。このような方法を、繰り返し二乗法と呼びます。
実際に10^{10}を分解すると、
10^{10} = 10^{8 + 2} = 10^8 \cdot 10^2
このようになります。
指数の肩が2の冪乗になる値を求めると、
\begin{split}
&10^2 \equiv 10^1 \cdot 10^1 \equiv 100 \pmod {2020}\\
&10^4 \equiv 10^2 \cdot 10^2 \equiv 100 \cdot 100 \equiv 1920 \pmod {2020}\\
&10^8 \equiv 10^4 \cdot 10^4 \equiv 1920 \cdot 1920 \equiv 1920 \pmod {2020}
\end{split}
このようになるので、10^{10} \equiv 10^8 \cdot 10^2 \equiv 1920 \cdot 100 \pmod {2020}と求まります。
a = 10
b = 10
mod = 2020
ans = 1
while b > 0:
if b % 2 == 1:
ans *= a
ans %= mod
a *= a
a %= mod
b //= 2
print(ans)
この方法だと、指数の肩をNとしてO(\log N)で答えが求まります。
実行時間
参考までに、指数の肩の大きさによる実行時間の違いを載せておきます。
|
10^2 |
10^4 |
10^6 |
10^8 |
| 愚直 |
2.98 \cdot 10^{-5} \mathrm{s} |
1.40 \cdot 10^{-3} \mathrm{s} |
0.110 \mathrm{s} |
9.88 \mathrm{s} |
| 繰り返し二乗法 |
2.02 \cdot 10^{-5} \mathrm{s} |
2.38 \cdot 10^{-5} \mathrm{s} |
2.67 \cdot 10^{-5} \mathrm{s} |
3.00 \cdot 10^{-5} \mathrm{s} |
一橋大学 2021年 大問1
1000以下の素数は250個以下であることを示せ。
数学解法
解法
1000以下の2, 3, 5の倍数の集合をそれぞれA, B, Cとする。
1000以下の素数2,3,5以外の2,3,5の倍数の集合Dの個数は、
\begin{split}
|D| &=|A \cup B \cup C| - 3\\
&= |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C| - 3\\
&= \left\lfloor \dfrac{1000}{2} \right\rfloor + \left\lfloor \dfrac{1000}{3} \right\rfloor + \left\lfloor \dfrac{1000}{5} \right\rfloor - \left\lfloor \dfrac{1000}{2\cdot3} \right\rfloor - \left\lfloor \dfrac{1000}{3\cdot5} \right\rfloor - \left\lfloor \dfrac{1000}{5 \cdot 2} \right\rfloor + \left\lfloor \dfrac{1000}{2\cdot3\cdot5} \right\rfloor - 3\\
&= 500 + 333 + 200 -166 -66 -100 + 33 - 3\\
&= 731
\end{split}
7,11,13,17,19,23,29から2つ選んでかけたものは1000以下の合成数であり、2,3,5の倍数ではない。
ゆえに、{}_7 C_2=21個はDに含まれない1000以下の合成数である。
以上より、1000以下の素数でない自然数は752個以上であるため、1000以下の素数は250個以下である。
別解
nと互いに素なn以下の自然数の個数を\varphi(n)とする。
nの素因数分解がn=\prod_{i=1}^{d}p_i^{e_i}と表されるとき、\varphi(n)=n\prod_{i=1}^{d}\left(1 - \dfrac{1}{p_i} \right)である。
ここで、1050=2\cdot3\cdot5^2\cdot7について考えると、
\varphi(1050)=1050\left(1 - \dfrac{1}{2}\right)\left(1 - \dfrac{1}{3}\right)\left(1 - \dfrac{1}{5}\right)\left(1 - \dfrac{1}{7}\right)=240
ゆえに、1050以下の素数の個数は、先ほどの結果に2,3,5,7を加えて244個以下である。
よって、明らかに1000以下の素数の個数は、250個以下である。
プログラミング解法
プログラミング解法では、1000以下の素数の個数を求めます。
愚直
1000以下のすべての自然数に対して、素数判定を行います。Nが素数か否かの判定は、2からN-1までのすべての自然数で割り切ることができないか否かで判定することができます。
N = 1000
ans = 0
for i in range(1, N + 1):
if i == 1:
continue
for j in range(2, i):
if i % j == 0:
break
else:
ans += 1
print(ans)
この方法だと、N以下の素数の個数はO(N^2)で求まります。
高速化1
先ほどの素数判定には無駄があります。2からN-1までのすべての自然数で割り切ることができないか判定していましたが、実は2から\lfloor\sqrt N\rfloorまでで十分です。
N = 1000
ans = 0
for i in range(1, N + 1):
if i == 1:
continue
for j in range(2, int(i ** 0.5) + 1):
if i % j == 0:
break
else:
ans += 1
print(ans)
この方法だと、N以下の素数の個数はO(N\sqrt N)で求まります。
高速化2
素数pが見つかったら、pを除くpの倍数をふるい落とすことで、合成数を消すことができます。これを次々と行うことで、最終的に素数だけを残すことができます。この方法をエラトステネスのふるいと呼びます。
試しに、30以下の素数をエラトステネスのふるいを使って求めてみましょう。
まず、2に素数ラベルをつけて、2を除く2の倍数をふるい落とします。

次に、3に素数ラベルをつけて、3を除く3の倍数をふるい落とします。

4はすでにふるい落とされているため飛ばします。
5に素数ラベルをつけて、5を除く3の倍数をふるい落とします。

この操作を繰り返し続けていくと、以下のようになります。
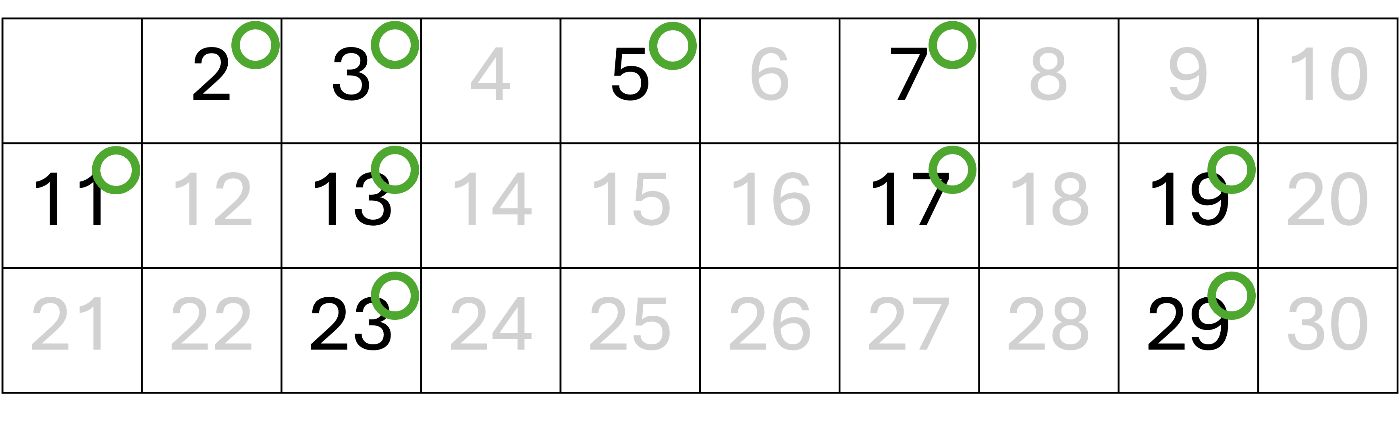
これで、30以下の素数は2,3,5,7,11,13,17,19,23,29であることがわかります。
N = 1000
ans = 0
P = [True] * (N + 1)
P[0] = False
P[1] = False
for i in range(N + 1):
if P[i]:
ans += 1
j = 2
while j * i <= N:
P[j * i] = False
j += 1
print(ans)
この方法だと、N以下の素数の個数はO(N\log{\log N})で求まります。
実は、高速化1と同じく、ふるい落とし操作は\lfloor\sqrt N\rfloorまでで十分です。このことも考慮すると、少しだけ速くすることができます。
実行時間
参考までに、素数判定する範囲による実行時間の違いを載せておきます。
|
10^2 |
10^4 |
10^6 |
10^8 |
| 愚直 |
9.08 \cdot 10^{-5} \mathrm{s} |
0.299\mathrm{s} |
1.98 \cdot 10^{3} \mathrm{s} |
- |
|
O(\sqrt N)素数判定 |
5.70 \cdot 10^{-5} \mathrm{s} |
9.03 \cdot 10^{-3} \mathrm{s} |
3.31 \mathrm{s} |
2.37 \cdot 10^{3} \mathrm{s} |
| エラトステネスのふるい |
4.20 \cdot 10^{-5} \mathrm{s} |
3.42 \cdot 10^{-3} \mathrm{s} |
0.346 \mathrm{s} |
63.3 \mathrm{s} |
京都大学 2022年 大問1
5.4<\log_4{2022}<5.5を示せ。ただし、0.301<\log_{10}{2}<0.3011
数学解法
解法
2000<2022<2048より、\log_4{2000}<\log_4{2022}<\log_4{2048}
\log_4{2048} = \log_4{2^{11}} = 11\log_4{2} = 11\cdot\dfrac{\log_2{2}}{\log_2{4}} = 11\cdot\dfrac{1}{2} = 5.5
\begin{split}
\log_4{2000} = \log_4{(2\cdot10^3)} = \log_4{2} + \log_4{10^3} = \log_4{2} + 3\log_4{10}\\
= \dfrac{\log_2{2}}{\log_2{4}} + 3 \cdot \dfrac{\log_{10}{10}}{\log_{10}{4}} = \dfrac{1}{2} + 3 \cdot \dfrac{1}{2\log_{10}{2}}\\ > \dfrac{1}{2} + 3 \cdot \dfrac{1}{2 \cdot 0.3011} > 5.4
\end{split}
以上より、5.4<\log_4{2022}<5.5
プログラミング解法
プログラミング解法では、4^x=2022となるxの近似値を求めます。なぜなら、\log_4{2022}=xとおくと、4^x=2022となるためです。
また、xの存在範囲はおよそわかっているものとします。
愚直
xがLからRまでの範囲に含まれているとします。LからRまで0.01刻みで4^xを計算して、2022を下回る最大値と上回る最小値を記録します。
from decimal import Decimal
a = 4
b = 2022
L = 0
R = 10
l_ans = 0
r_ans = 10
x = Decimal(L)
while L <= x <= R:
if 4 ** x < b:
l_ans = max(l_ans, x)
else:
r_ans = min(r_ans, x)
x += Decimal('0.01')
print(f'{l_ans}<log_{a}({b})<{r_ans}')
この方法だと、xの存在範囲の大きさをNとしてO(N)で近似値が求まります。
高速化
先ほどの方法には無駄があります。4^xは単調増加するので、小さい値から順番に4^xが2022よりも小さいかどうかを確かめるのは無駄が多いです。探索範囲の半分の場所で4^xが2022よりも小さいかどうかを確かめれば、探索範囲を半分にすることができます。この方法を二分法と呼びます。
実際に、二分法を行なっている様子を見てみましょう。
まず、xの存在範囲の左端をL=0、右端をR=10とします。
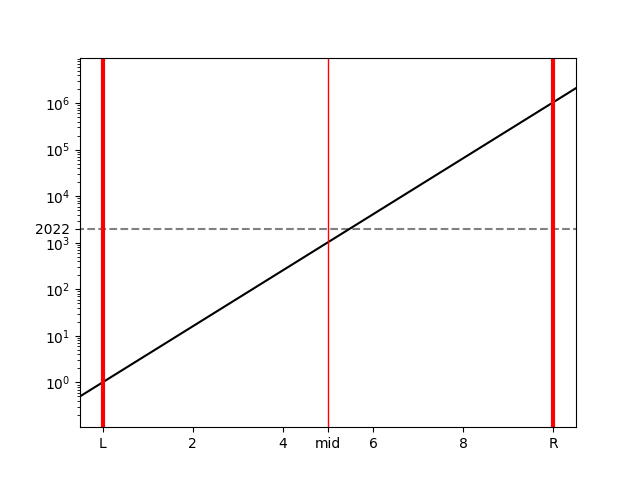
xの存在範囲の中心 \text{mid}=5について、4^{\text{mid}}は2022よりも小さいので、L=\text{mid}=5とします。
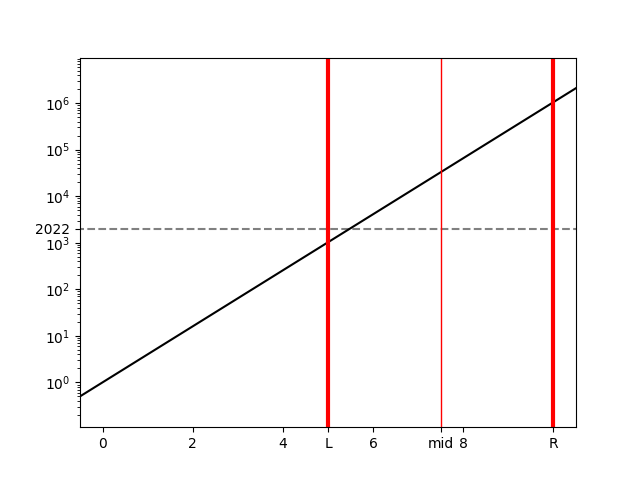
次に、xの存在範囲の中心 \text{mid}=7.5について、4^{\text{mid}}は2022よりも大きいので、R=\text{mid}=7.5とします。
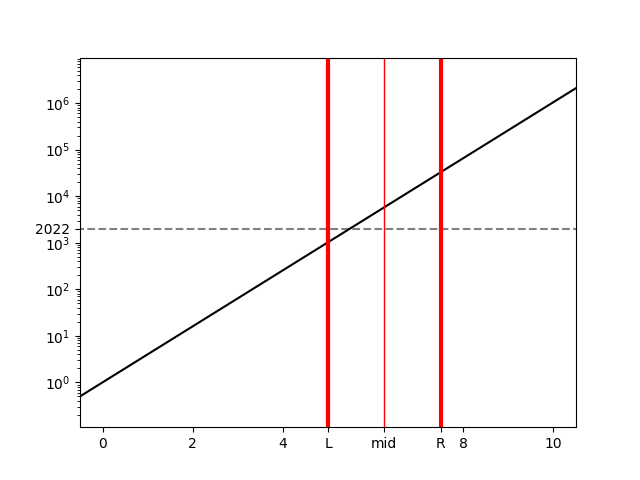
さらに、xの存在範囲の中心 \text{mid}=6.25について、4^{\text{mid}}は2022よりも大きいので、R=\text{mid}=6.25とします。

この操作を繰り返していくと、xの存在範囲を半分ずつ縮めながらxの近似値を求めることができます。
from decimal import Decimal
a = 4
b = 2022
l_ans = Decimal('0')
r_ans = Decimal('10')
while (r_ans - l_ans) > Decimal('0.01'):
mid = (l_ans + r_ans) / 2
if 4 ** mid < b:
l_ans = mid
else:
r_ans = mid
print(f'{l_ans}<log_{a}({b})<{r_ans}')
この方法だと、xの存在範囲の大きさをNとしてO(\log N)で近似値が求まります。
実行時間
参考までに、xの存在範囲の大きさによる実行時間の違いを載せておきます。
|
10^1 |
10^2 |
10^3 |
10^4 |
10^5 |
| 愚直 |
5.80 \cdot 10^{-2} \mathrm{s} |
0.562 \mathrm{s} |
5.65 \mathrm{s} |
57.2 \mathrm{s} |
575 \mathrm{s} |
| 二分法 |
7.92 \cdot 10^{-4} \mathrm{s} |
1.01 \cdot 10^{-3} \mathrm{s} |
1.30 \cdot 10^{-3} \mathrm{s} |
1.43 \cdot 10^{-3} \mathrm{s} |
1.64 \cdot 10^{-3} \mathrm{s} |
まとめ
この記事では、受験数学をプログラミングで倒すとともに、そのプログラムの高速化の方法について解説しました。これらの高速化は、競技プログラミングでもよく使うテクニックなので、ぜひ他の例でも試して習得してみてください。
追記
この記事の続編を書きました。
https://zenn.dev/luna_moonlight/articles/7ef35d0a56d4e4



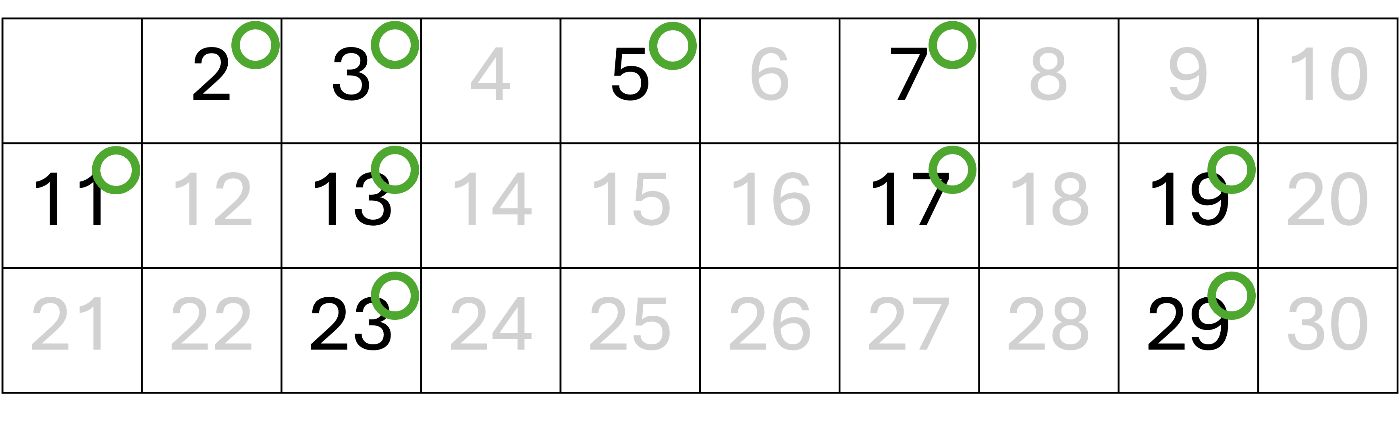




Discussion