[ABC263] AtCoder Beginner Contest 263(A-E 問題 Python)
AtCoder Beginner Contest 263 の復習記録です。
A問題からE問題までやります。使用言語はPythonです。
A問題
考え方
カードの番号ごとに、枚数をカウントしておき、降順に並び替えます。
1番目に多い枚数
提出コード
num = list(map(int,input().split()))
card = [0]*13
for n in num:
card[n-1] += 1
card.sort(reverse=True)
if card[0] == 3 and card[1] == 2:
ans = "Yes"
else:
ans = "No"
print(ans)
B問題
考え方
Pのインデックスが
提出コード
N = int(input())
P = list(map(int,input().split()))
ans = 0
while N > 1:
N = P[N-2]
ans += 1
print(ans)
C問題
考え方
深さ優先探索(DFS)で調べました。リストに始めから
提出コード
import sys; sys.setrecursionlimit(10**6)
N,M = map(int,input().split())
def dfs(num,k):
if k > N:
print(*num[1:])
return
for i in range(num[-1]+1,M+1):
dfs(num+[i],k+1)
dfs([0],1)
D問題
考え方
問題文を読み解くと
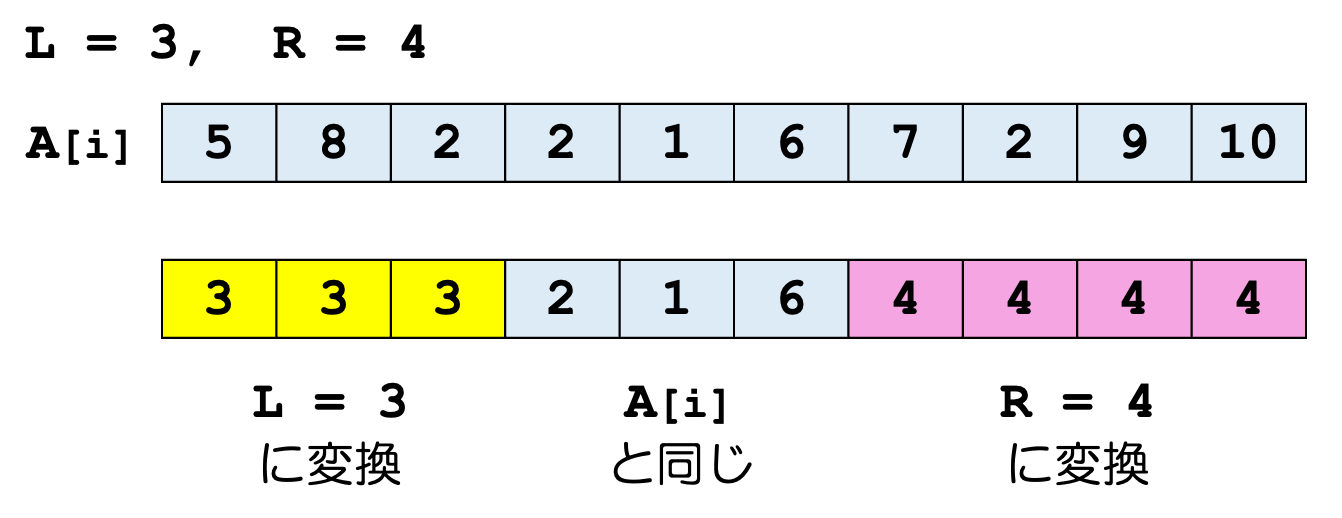
下記のようにdpを考えてみます。
| dp | 定義 |
|---|---|
| dpL[ |
|
| dpA[ |
|
| dpR[ |
|
dpL[
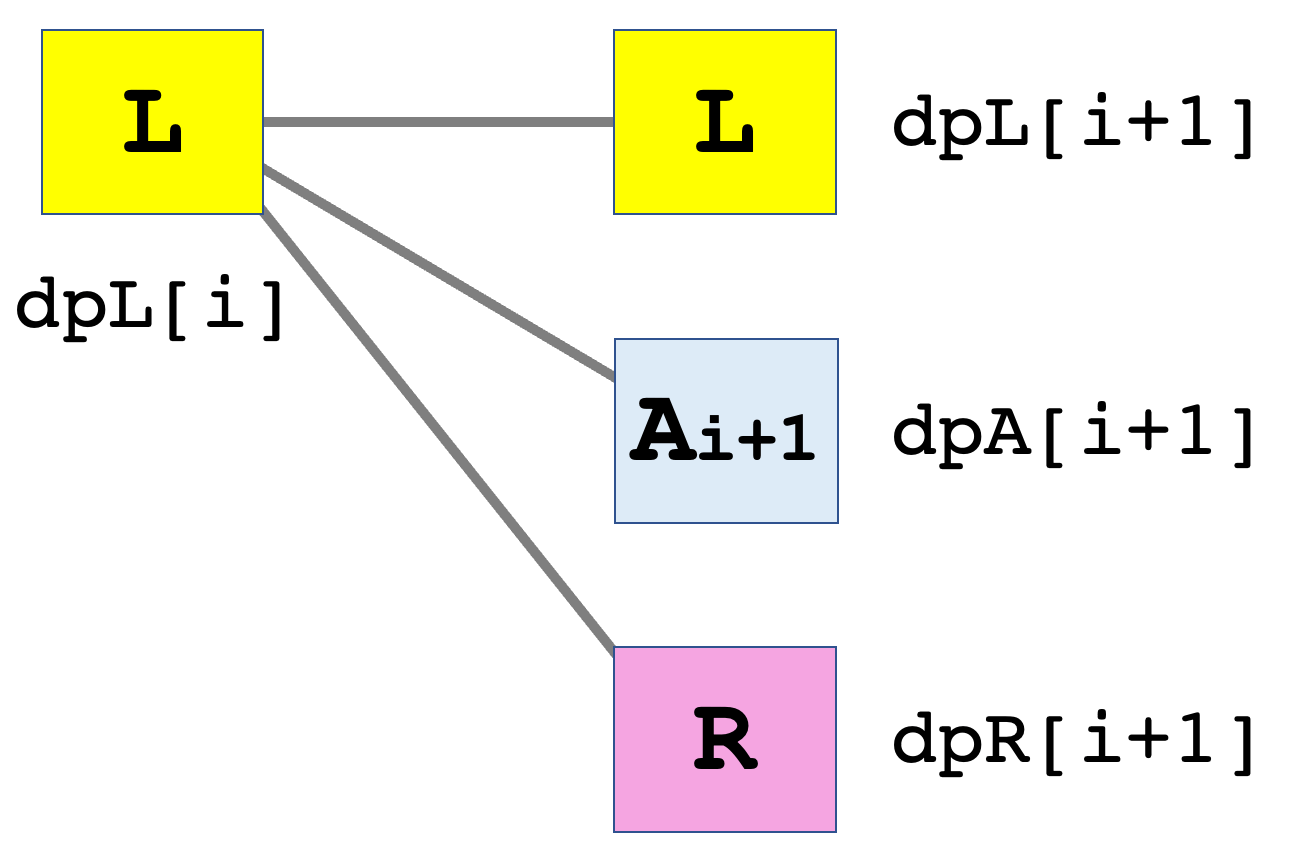
dpA[
dpR[
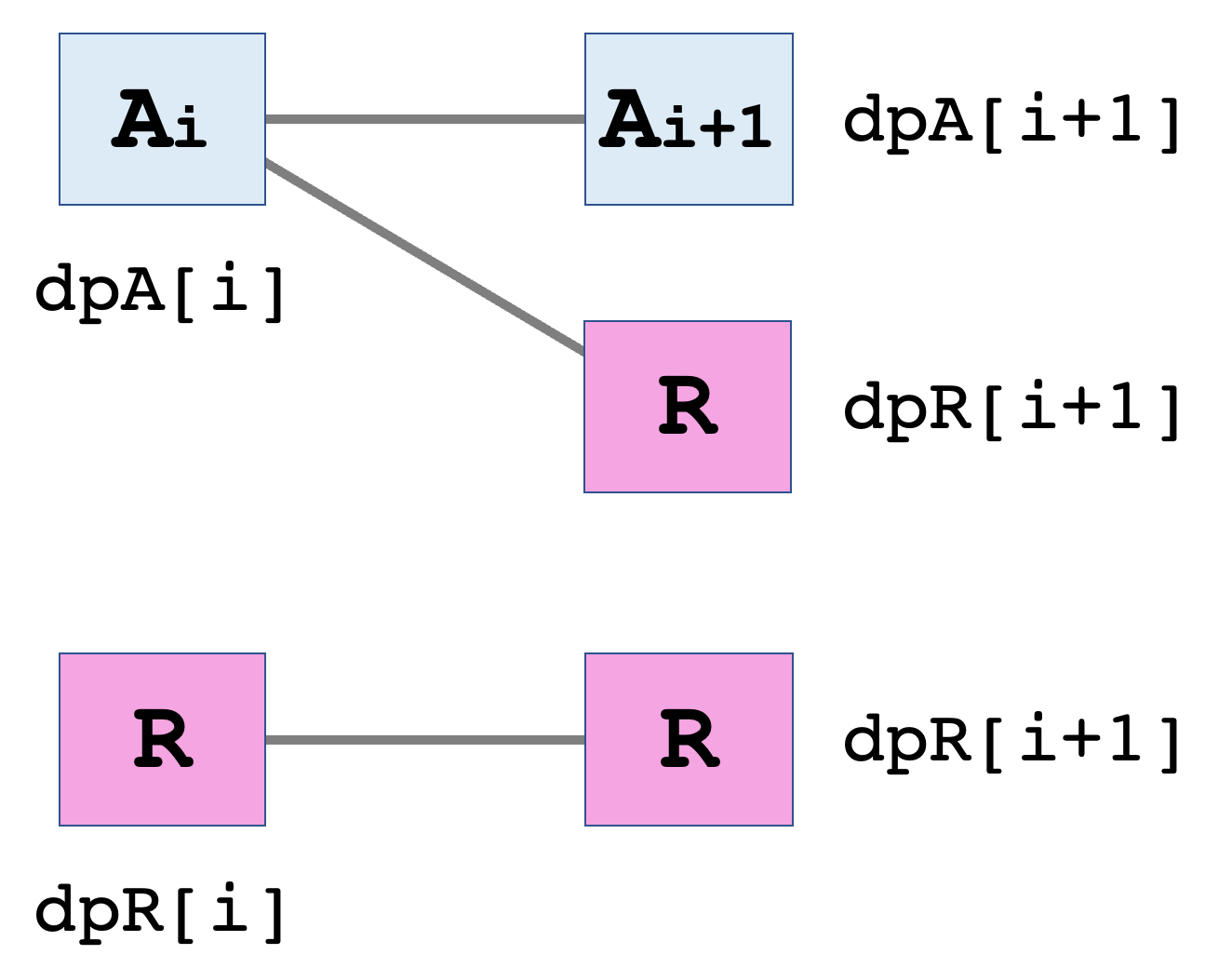
提出コード
N,L,R = map(int,input().split())
A = list(map(int,input().split()))
dpR = [R*(N-i) for i in range(N)]
dpA = [0] * N
dpL = [0] * N
dpA[-1] = A[-1]
dpL[-1] = L
for i in range(N-1,0,-1):
dpA[i-1] = A[i-1] + min(dpA[i], dpR[i])
dpL[i-1] = L + min(dpL[i], dpA[i], dpR[i])
ans = min(dpL[0],dpA[0],dpR[0])
print(ans)
E問題
考え方
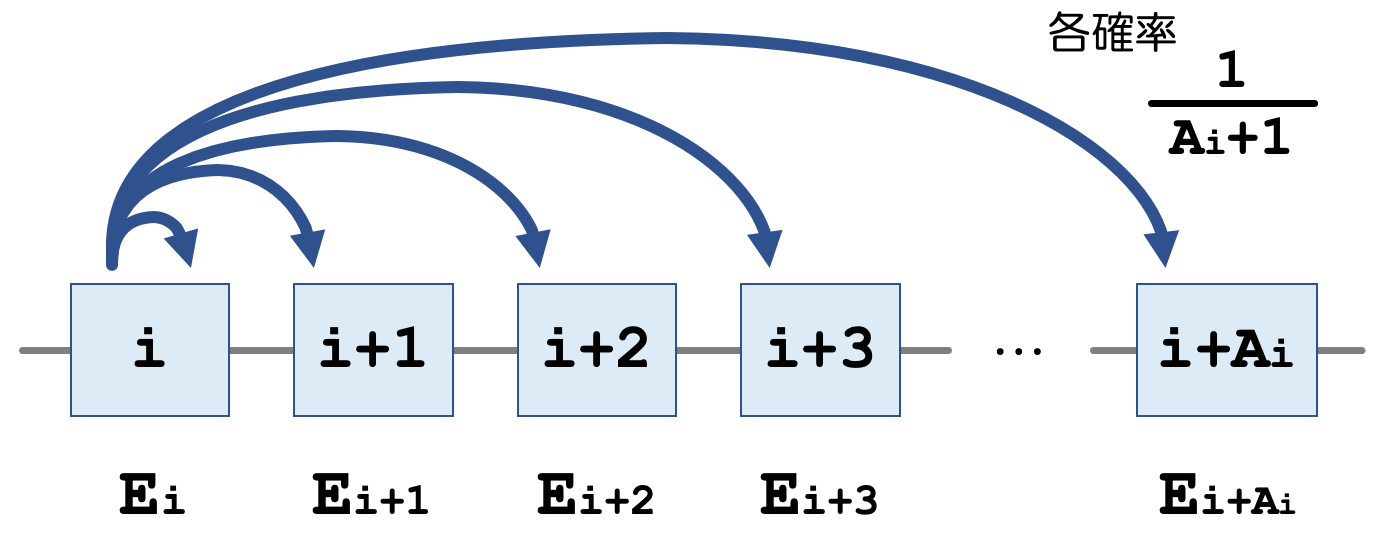
これを式変形していきます。
あとは、逆元を用いて実装すれば良いです。逆元はフェルマーの小定理を用います。
提出コード (TLE)
# TLEになるコード
MOD = 998244353
N = int(input())
A = list(map(int,input().split()))
E = [0]*N
for i in range(N-2,-1,-1):
s = A[i]+1
for k in range(1,A[i]+1):
s += E[i+k]
s %= MOD
s *= pow(A[i], MOD-2, MOD)
s %= MOD
E[i] = s
print(E[0])
上記のコードがTLEになるのは、二重forループの部分で計算量が増えているからです。この部分について、累積和を用いて高速化します。マス
提出コード (AC)
MOD = 998244353
N = int(input())
A = list(map(int,input().split()))
E = [0]*N
acc = [0]*(N+1)
for i in range(N-2,-1,-1):
s = A[i]+1
s += acc[i+1]-acc[i+A[i]+1]
s %= MOD
s *= pow(A[i], MOD-2, MOD)
s %= MOD
E[i] = s
acc[i] = E[i] + acc[i+1]
print(E[0])
Discussion