🚀

ABC108 B - Ruined Squareのメモ

2024/05/12に公開

AtCoder

全くわからんので解説を咀嚼します。

以下は入力例2をもとに考えてみます。

ベクトルについて

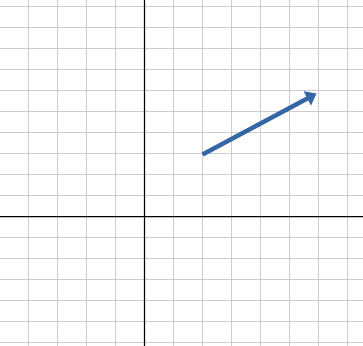
ベクトルとは、向きと大きさを持つ何かです。始点と終点があり、それを結ぶ直線矢印で表します。大きさは長さで表現します。
例の直線について、 $(x1, y1)$ を始点とするベクトルで表現してみると以下のような感じです。

ベクトルは位置には依存せず、向きと大きさが同じなら同じベクトルです。したがって座標平面上で任意の平行移動ができます。たとえば始点を原点に移動させてみます。

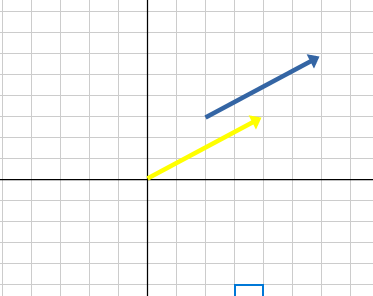
この時、移動後のベクトルの終点の座標は $(4, 3)$ となっていますが、これをベクトルの成分表示といいます。始点が原点と決まっていれば、あとは終点の座標さえわかればベクトルの向きも大きさもわかる、つまりベクトルを特定できます。 $(4, 3)$ がベクトルの識別子になるわけですね。

ということで、解説の初手で $(x2 - x1, y2 - y1)$ を求めているのはこのベクトルの成分表示を求めています。例だと $(6 - 2, 6 - 3)$ なのでたしかに $(4, 3)$ になります。成分表示を求めているのは、後述の回転行列がそれ前提だからのようです。

回転行列について

さて、ここで $(4, 3)$ を反時計回りに90°回転させたいです。もっと言うと、回転後のベクトルの成分表示がほしい。まさにそれを求めることができるのが回転行列です。 $(x, y)$ のベクトルを反時計回りにθだけ回転させた後の座標 $(x', y')$ は以下の式で求められます。

\begin{pmatrix} x' \\ y' \\ \end{pmatrix} = \begin{pmatrix} cosθ & −sinθ \\ sinθ & cosθ \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix}

回転行列というだけあって、行列で表現します。
これは

\begin{pmatrix} cosθ & −sinθ \\ sinθ & cosθ \\ \end{pmatrix}

\begin{pmatrix} x \\ y \\ \end{pmatrix}

という2つの行列を掛けた結果ということですね。
後者は座標なので

\begin{pmatrix} 4 \\ 3 \\ \end{pmatrix}

です。

$sinθ$ とか $cosθ$ ですが、今回はθは90°です。90°の場合、 $sinθ$ は1で $cosθ$ は0です。なので

\begin{pmatrix} 0 & −1 \\ 1 & 0 \\ \end{pmatrix}

です。
したがって

\begin{pmatrix} 0 & −1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 4 \\ 3 \\ \end{pmatrix}

を計算した結果がほしい値です。

行列の掛け算はあまり直感的ではない計算方法になります。

\begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix} = \begin{pmatrix} ax + by \\ cx + dy \\ \end{pmatrix}

となるらしいです。今回は

\begin{pmatrix} 0 & −1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 4 \\ 3 \\ \end{pmatrix} = \begin{pmatrix} 0 × 4 + -1 × 3 \\ 1 × 4 + 0 × 3 \\ \end{pmatrix} = \begin{pmatrix} -3 \\ 4 \\ \end{pmatrix}

となります。

なので $(4, 3)$ のベクトルを反時計回りに90°回転させると、 $(-3, 4)$ になります。

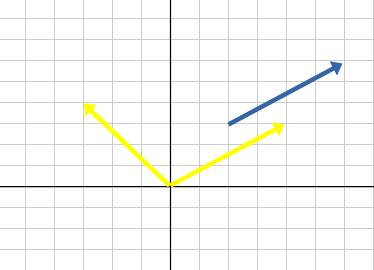
（あんまり90°っぽく見えないのはこの座標が雑に作ったものだからです…）

ただ、 $(-3, 4)$ はまだ答えではありません。ほしい値のベクトルの始点は原点ではなく $(6, 6)$ です。 $(-3 + 6, 4 + 6) = (3, 10)$ がほしい答えの1つ目です。（これはベクトルの平行移動です）

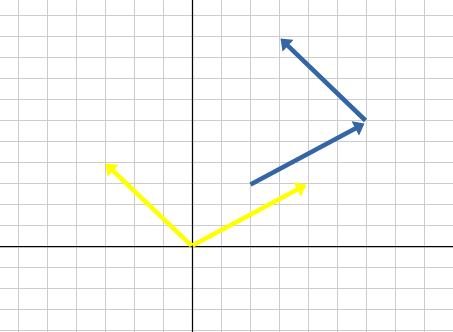
ほしい値の2つ目を得るには、回転後のベクトルをさらに90°回転させます。すなわち

\begin{pmatrix} 0 & −1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} -3 \\ 4 \\ \end{pmatrix} = \begin{pmatrix} 0 × -3 + -1 × 4 \\ 1 × -3 + 0 × 4 \\ \end{pmatrix} = \begin{pmatrix} -4 \\ -3 \\ \end{pmatrix}

です。

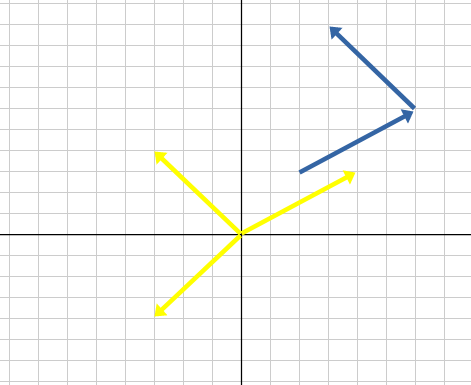
どう見ても歪んでるけど脳内補正をお願いします…本来はまっすぐになるはず。
で、これをまた平行移動させます。今度は始点が $(3, 10)$ なので、 $(-4 + 3, -3 + 10) = (-1, 7)$ です。

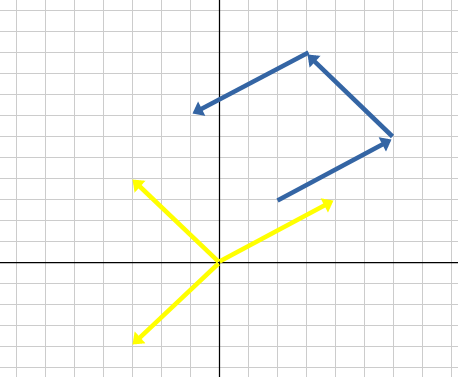
ということで求める答えは $(3, 10)$ および $(-1, 7)$ です。出力例と一致しました。

実装

fun main() {
    val (x1, y1, x2, y2) = readln().split(" ").map { it.toInt() }

    // ベクトルの始点を原点へ（成分表示）
    var dx = x2 - x1
    var dy = y2 - y1

    var x = x2
    var y = y2

    for(i in 0 until 2) {
        // 回転
        val rdx = -dy
        val rdy = dx

        // 始点を原点からx2, y2(もしくはx3, y3)に平行移動
        x = rdx + x
        y = rdy + y

        print("$x $y")
        if(i == 0) {
            print(" ")
        }

        dx = rdx
        dy = rdy
    }
    println()
}

ベクトルについて

回転行列について

実装

Discussion