ディリクレ分布から中華料理店過程の分割ルールを導出する

$$\gdef\ds{\displaystyle} \gdef\b#1{\mathbf{#1}} \gdef\bs#1{\boldsymbol{#1}}$$

まえがき

ディリクレ分布から中華料理店仮定（CRP）の分割ルールを導出します。CRPの詳細は参考にさせて頂いた『続・わかりやすい　パターン認識 －教師なし学習入門－』を参照してください。

前準備

• サンプルの数を$n$とします。
• クラスタの数を$c$（ただし$n << c$）とし、各クラスタを$\omega_j \; (j = 1, \ldots, c)$で表現します。
• 各サンプルへのクラスタの割り当てを$s_k$として表現します。$s_k$は1つのクラスタのみに属するとします。
• $s_k$に$\omega_i$が割り当てられる確率を$\pi_i$とします。$\sum_{j = 1}^c \pi_j = 1$です。
• $\bs{\pi} = \left[\pi_1, \ldots, \pi_c \right]^\top, \bs{\alpha} = \left[\alpha_1, \ldots, \alpha_c \right]^\top$という表記を用います。
• $\bs{\pi}$の確率分布として、以下のようにディリクレ分布を仮定します。

$$p(\bs{\pi}) = \mathrm{Dir} ( \bs{\pi} | \bs{\alpha} ) = \frac{\Gamma\left(\sum_{j = 1}^c \alpha_j \right)}{\prod_{j = 1}^c \Gamma (\alpha_j)} \prod_{j = 1}^c \pi_j^{\alpha_j - 1}$$

• $\bs{\pi}$が与えられたとき、$s_k$はカテゴリ分布に従うと考えられます。

$$p(s_k = \omega_i | \bs{\pi}) = \mathrm{Cat} (s_k = \omega_i | \bs{\pi}) = \pi_i$$

導出

事前に、今回想定しているグラフィカルモデルを示します。$\bs{\alpha}$から$\bs{\pi}$が確率的に生成され、$\bs{\pi}$から$s_1, \ldots, s_n$が生成されるという構造になっています。

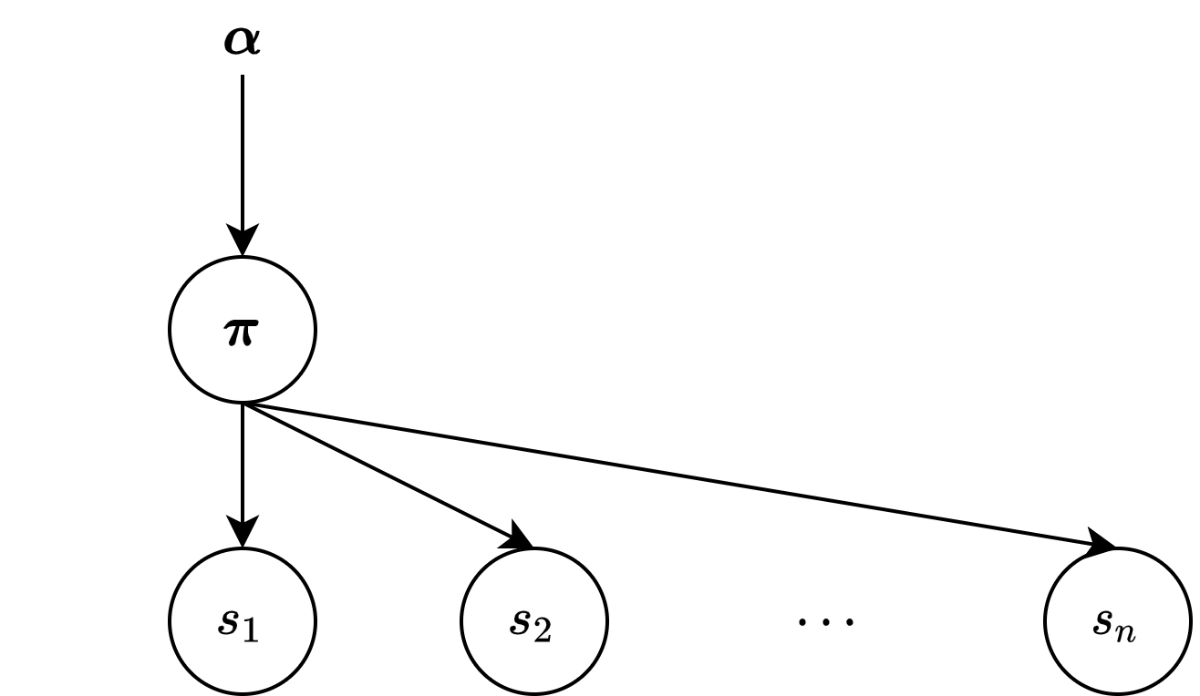
想定するグラフィカルモデル

CRPの分割ルールを導出するため、$s_1, \ldots, s_{n - 1}$が与えられたとき、$s_n$があるクラスタ$\omega_i$に割り当てられる確率$p(s_n = \omega_i | s_1, \ldots, s_{n - 1})$を求めます。$\bs{\alpha}$は与えられていますが、$\bs{\pi}$は未知です。ここで、1つのパラメータ$\alpha$を用いて各クラスタの$\alpha_j = \alpha / c$として、全て等しいとします。このとき、$p(\bs{\pi})$は

$$p(\bs{\pi}) = \mathrm{Dir} ( \bs{\pi} | \alpha ) = \frac{\Gamma(\alpha)}{\Gamma (\alpha / c)^c} \prod_{j = 1}^c \pi_j^{\alpha / c - 1}$$

となっています。$s_1, \ldots, s_{n - 1}$の中で$\omega_j$に割り当てられた個数を$n_j$とすると、

$$p(s_1, \ldots, s_{n - 1} | \bs{\pi}) = \prod_{k = 1}^{n - 1} p(s_k | \bs{\pi}) = \prod_{j = 1}^c \pi_j^{n_j}$$

です。これを用いて$p(s_n = \omega_i | s_1, \ldots, s_{n - 1})$を求めます。

$$\begin{aligned} p(s_n = \omega_i | s_1, \ldots, s_{n - 1}) = \frac{p(s_n = \omega_i, s_1, \ldots, s_{n - 1})}{p(s_1, \ldots, s_{n - 1})} \end{aligned}$$

計算が煩雑になるため、まずは分母$p(s_1, \ldots, s_{n - 1})$を求めます。$\bs{\pi}$についての周辺化を考慮することで

$$\begin{aligned} & p(s_1, \ldots, s_{n - 1}) \\ &= \int p(s_1, \ldots, s_{n - 1}, \bs{\pi}) d \bs{\pi} = \int p(s_1, \ldots, s_{n - 1} | \bs{\pi}) p(\bs{\pi}) d \bs{\pi} \\ &= \int \left\{ \prod_{j = 1}^c \pi_j^{n_j} \right\} \frac{\Gamma(\alpha)}{\Gamma(\alpha / c)^c} \prod_{j = 1}^c \pi_j^{\alpha / c - 1} d \bs{\pi} = \int \frac{\Gamma(\alpha)}{\Gamma(\alpha / c)^c} \prod_{j = 1}^c \pi_{j}^{n_j + \alpha / c - 1} d \bs{\pi} \\ &= \frac{\Gamma(\alpha)}{\Gamma(\alpha / c)^c} \frac{\prod_{j = 1}^c \Gamma(n_j + \alpha / c)}{\Gamma(\sum_{j = 1}^c (n_j + \alpha / c))} \quad \left(\because \mathrm{補足を参照してください} \right) \\ &= \frac{\Gamma(\alpha)}{\Gamma(\alpha / c)^c} \frac{\prod_{j = 1}^c \Gamma(n_j + \alpha / c)}{\Gamma(n - 1 + \alpha)} \quad \left(\because \sum_{j = 1}^c n_j = n - 1, \sum_{j = 1}^c \alpha / c = \alpha \right) \\ &= \frac{\Gamma(\alpha)}{\Gamma(n - 1 + \alpha)} \prod_{j = 1}^c \frac{\Gamma(n_j + \alpha / c)}{\Gamma(\alpha / c)} \end{aligned}$$

が得られます。分子$p(s_n = \omega_i, s_1, \ldots, s_{n - 1})$では$s_1, \ldots, s_{n - 1}$に加えて$s_n = \omega_i$となる確率を求めることになります。これは分母$p(s_1, \ldots, s_{n - 1})$を求めるときと同様の手順によって式変形を行うことにより、

$$\begin{aligned} & p(s_n = \omega_i, s_1, \ldots, s_{n - 1}) \\ &= \int p(s_n = \omega_i, s_1, \ldots, s_{n - 1}, \bs{\pi}) d \bs{\pi} = \int p(s_n = \omega_i, s_1, \ldots, s_{n - 1} | \bs{\pi}) p(\bs{\pi}) d \bs{\pi} \\ &= \int p(s_n = \omega_i | \bs{\pi}) \left\{ \prod_{k = 1}^{n - 1} p(s_k | \bs{\pi}) \right\} p(\bs{\pi}) d \bs{\pi} \\ &= \frac{\Gamma(\alpha)}{\Gamma(n + \alpha)} \frac{\Gamma(n_i + 1 + \alpha / c)}{\Gamma(\alpha / c)} \left\{ \prod_{\substack{j = 1 \\ j \neq i}} \frac{\Gamma(n_j + \alpha / c)}{\Gamma(\alpha / c)} \right\} \end{aligned}$$

となります。したがって、求めたい$p(s_n = \omega_i | s_1, \ldots, s_{n - 1})$は

$$\begin{aligned} & p(s_n = \omega_i | s_1, \ldots, s_{n - 1}) \\ &= \frac{p(s_n = \omega_i, s_1, \ldots, s_{n - 1})}{p(s_1, \ldots, s_{n - 1})} \\ &= \frac{\Gamma(\alpha)}{\Gamma(n + \alpha)} \frac{\Gamma(n_i + 1 + \alpha / c)}{\Gamma(\alpha / c)} \left\{ \prod_{\substack{j = 1 \\ j \neq i}} \frac{\Gamma(n_j + \alpha / c)}{\Gamma(\alpha / c)} \right\} \cdot \frac{\Gamma(n - 1 + \alpha)}{\Gamma(\alpha)} \prod_{j = 1}^c \frac{\Gamma(\alpha / c)}{\Gamma(n_j + \alpha / c)} \\ &= \frac{\bcancel{\Gamma(\alpha)}}{\Gamma(n + \alpha)} \frac{\Gamma(n_i + 1 + \alpha / c)}{\bcancel{\Gamma(\alpha / c)}} \left\{ \prod_{\substack{j = 1 \\ j \neq i}} \frac{\Gamma(n_j + \alpha / c)}{\bcancel{\Gamma(\alpha / c)}} \right\} \cdot \frac{\Gamma(n - 1 + \alpha)}{\bcancel{\Gamma(\alpha)}} \prod_{j = 1}^c \frac{\bcancel{\Gamma(\alpha / c)}}{\Gamma(n_j + \alpha / c)} \\ &= \frac{\Gamma(n - 1 + \alpha)}{\Gamma(n + \alpha)} \frac{\Gamma(n_i + 1 + \alpha / c)}{\Gamma(n_i + \alpha / c)} \\ &= \frac{1}{n - 1 + \alpha} \cdot (n_i + \alpha / c) = \frac{n_i + \alpha / c}{n - 1 + \alpha} \end{aligned}$$

と計算することができます。

$c$個の全てのクラスタを含む集合を$\Omega$とします。ここで、$n << c$と仮定していることから、$n_i = 0$、即ち1つも属するサンプルが存在しないクラスタが存在します。$\Omega$を1つも属するサンプルが存在しないクラスタの集合$\Omega_0 = \left\{\omega_i | n_i = 0, i = 1, \ldots, c \right\}$およびそれ以外のクラスタの集合$\Omega_1 = \left\{\omega_i | n_i \neq 0, i = 1, \ldots, c \right\}$に分割します。つまり$\Omega = \Omega_0 \cup \Omega_1, \emptyset = \Omega_0 \cap \Omega_1, c = |\Omega| = |\Omega_1| + |\Omega_2|$です。
このとき、

$$\begin{aligned} & p(s_n \in \Omega_0 | s_1, \ldots, s_{n - 1}) = \sum_{\omega_i \in \Omega_0} p(s_n = \omega_i | s_1, \ldots, s_{n - 1}) = \sum_{\omega_i \in \Omega_0} \frac{n_i + \alpha / c}{n - 1 + \alpha} \\ &= \sum_{\omega_i \in \Omega_0} \frac{\alpha / c}{n - 1 + \alpha} = \frac{c - |\Omega_1|}{c} \frac{\alpha}{n - 1 + \alpha} \end{aligned}$$

であり、$c \rightarrow \infty$の極限では

$$\begin{aligned} & p(s_n \in \Omega_0 | s_1, \ldots, s_{n - 1}) = \left(1 - \frac{|\Omega_1|}{c} \right) \frac{\alpha}{n - 1 + \alpha} \rightarrow \frac{\alpha}{n - 1 + \alpha} \quad (c \rightarrow \infty) \end{aligned}$$

です。一方、$\Omega_1$に属するクラスタに対しては

$$p(s_n = \omega_i \in \ \Omega_1 | s_1, \ldots, s_{n - 1}) = \frac{n_i + \alpha / c}{n - 1 + \alpha} \rightarrow \frac{n_i}{n - 1 + \alpha} \quad (c \rightarrow \infty)$$

です。以上の計算をまとめると

$$\begin{cases} \ds p(s_n \in \Omega_0 | s_1, \ldots, s_{n - 1}) = \frac{\alpha}{n - 1 + \alpha} \\ \\ \ds p(s_n = \omega_i \in \ \Omega_1 | s_1, \ldots, s_{n - 1}) = \frac{n_i}{n - 1 + \alpha} \end{cases}$$

となります。$s_n$が$n_i \neq 0$の既存のクラスタ$\omega_i \in \Omega_1$のいずれかに属する確率と$s_n$が$n_i = 0$の新規のクラスタ$\omega_i \in \Omega_0$に属する確率は$n_i : \alpha$の比になっています。したがって、これはCRPの分割ルールに対応していることが分かります。

補足

$$\int \prod_{j = 1}^c \pi_{j}^{n_j + \alpha / c - 1} d \bs{\pi} = \frac{\prod_{j = 1}^c \Gamma(n_j + \alpha / c)}{\Gamma(\sum_{j = 1}^c (n_j + \alpha / c))}$$

を示します。
$\bs{\tilde{\alpha}} = \left[n_1 + \alpha / c, \ldots, n_c + \alpha / c \right]^\top$とすると、$\bs{\tilde{\alpha}}$をパラメータとするディリクレ分布は

$$\mathrm{Dir} (\bs{\pi} | \bs{\tilde{\alpha}}) = \frac{\Gamma(\sum_{j = 1}^c (n_j + \alpha / c))}{\prod_{j = 1}^c \Gamma(n_j + \alpha / c)} \prod_{j = 1}^c \pi_{j}^{n_j + \alpha / c - 1}$$

と表せます。ディリクレ分布は確率分布なので、$\bs{\pi}$で積分すると1になります。

$$\begin{aligned} \int \mathrm{Dir} (\bs{\pi} | \bs{\tilde{\alpha}}) d \bs{\pi} &= \int \frac{\Gamma(\sum_{j = 1}^c (n_j + \alpha / c))}{\prod_{j = 1}^c \Gamma(n_j + \alpha / c)} \prod_{j = 1}^c \pi_{j}^{n_j + \alpha / c - 1} d \bs{\pi} \\ &= \frac{\Gamma(\sum_{j = 1}^c (n_j + \alpha / c))}{\prod_{j = 1}^c \Gamma(n_j + \alpha / c)} \int \prod_{j = 1}^c \pi_{j}^{n_j + \alpha / c - 1} d \bs{\pi} \\ &= 1 \end{aligned}$$

分数の中には$\bs{\pi}$を含んでいないため、積分の対象にはなっていません。よって、この結果から

$$\int \prod_{j = 1}^c \pi_{j}^{n_j + \alpha / c - 1} d \bs{\pi} = \frac{\prod_{j = 1}^c \Gamma(n_j + \alpha / c)}{\Gamma(\sum_{j = 1}^c (n_j + \alpha / c))}$$

が得られます。

参考文献

• 『続・わかりやすい　パターン認識 －教師なし学習入門－』
  • https://shop.ohmsha.co.jp/shopdetail/000000000574/