拡散モデルと表データ生成③:【論文】STaSy
STaSy: Score-based Tabular Data Synthesis (ICLR2023)
TabDDPM, CoDiに続いてSTaSyの論文を読んだので, そのまとめになります. まとめと言いつつかなり長くなっています. 図や表は断りのない限り論文からの引用です. これまではICMLの論文でしたが, 今回はICLRの論文です.
arXiv
OpenReview
書籍情報
Kim, J., Lee, C., and Park, N. STasy: Score-based tabular data synthesis. In The Eleventh International Conference on Learning Representations, 2023.
関連情報
TL;DR
- スコアベースの表データ生成モデルの提案
- self-paced trainingとfine-tuningを経ることで訓練を安定化させ, 高品質生成を実現
- 15のデータセットと7つのベースラインを用いた比較ではqualityとdiversityで既存手法を凌駕
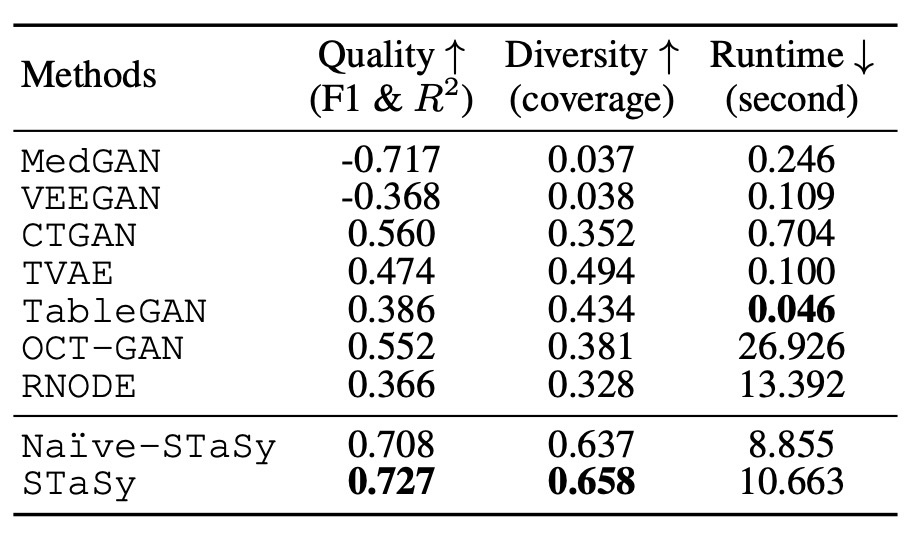
まず, 実験のまとめを見てみます. 全データセットの平均を報告しています. これを見ると, 確かに高品質で多様性のあるデータ生成がされていることがわかります (CoDiのときと同様speedはイマイチです).
提案手法は3つの大きな特徴があり, それらを順番に見ていきます.
- スコアベースのモデル
- self-paced learning
- fine-tuning approach
スコアベースのモデル
まず, スコアベースのモデルを表データに適用する前に, 拡散モデルのスコアベースとしての見方をしておきます. 以下の論文などが参考になります.
DDPMをベースとした定式化は, 以下のIto SDEに従います.
ここで, DDPMの場合には
ここで,
今回は最初からスコアネットワークを学習することを考えます. すると, 以下の式を満たすネットワークを求めることになります.
さて, これを表データ生成に適用することを考えます. 表データの特徴は以下の3つです.
- 表データは複雑な分布をしていて, 難易度が高い
- 一方で次元数は非常に低い (例えばMNISTでは784ピクセルですが, 実験で用いているデータの1つであるCreditは30カラム程度しかありません)
- カラム間の結合確率がある (カラム同士の関係性が決まっています)
スコアネットワークが十分に学習されている場合に, この壁を越えられるようです.
論文にモデルの概要図などはありませんが, スコアネットワークの設計が示されているので見てみます. ネットワークは全結合層の残差接続で構成されています.
入力は, 数値データをmin-max scaler, カテゴリデータをone-hot encodingで前処理しています.
self-paced learning
self-paced learning (SPL)を用いて事前学習を行います. SPLとは, カリキュラム学習に関連する訓練戦略のひとつです. カリキュラム学習とは, 学習中のモデルに与えるデータを制御することで効率的に訓練を行う手法で, 例えば簡単なデータを最初に与えて徐々に難易度を上げるなどがあります. モデルは以下の目的関数を最小化します.
です. そのため, STaSyの目的関数は
です.
正規化関数
をdenoising score matchingの目的関数のCDF (累積分布関数)としたときに, 関数 F を, Q(p) で定めます. すなわち, \inf \{l\in\mathbb{R}: p\leq F(l)\} は与えられた確率 Q(p) よりCDFが大きいか等しい最小値です. p
このとき, 正規化関数を
とします. このとき,
証明はここでは省略しますが, Appendix Eに記載されています (
この式を具体的にみます.
Fine-Tuning Approach
self-paced learningによる学習が終わったら, パラメータを微調整するフェーズに入ります.
逆拡散過程のSDEによるアプローチとして, さまざまな数値解法があります. そのうちの1つにprobabilistic flowがあります. そこでは次のNODE (Neural ODE)を用います.
NODEは対数確率を計算するのに有用なので, 正確な対数確率に基づいたfine-tuningを行います.
パラメータ
実験
15のデータと7つのベースラインを用いて実験を行います. 今回は, 普通にスコアベースのモデルを訓練したNaive-STaSyとself-paced learningとfine-tuningを行うSTaSyを提案手法として区別しています.
評価方法としてTSTR frameworkを用います. 生成品質については分類データに対してはaverage F1を主に使い, 補助的に AUROCとWeighted-F1を用います. 回帰データに対しては
それぞれ結果を見てみます.
Sampling Quality
MedGANとVEEGANは2017年のモデルでかなり初期のもののため, 生成品質は非常に低いです. また, ベースラインの中ではCTGANとOCT-GANが高性能ですが, 今回提案された手法の方が良い結果になっています.

個別のデータについて少し見ていきます. まず, 多クラス分類のデータです.
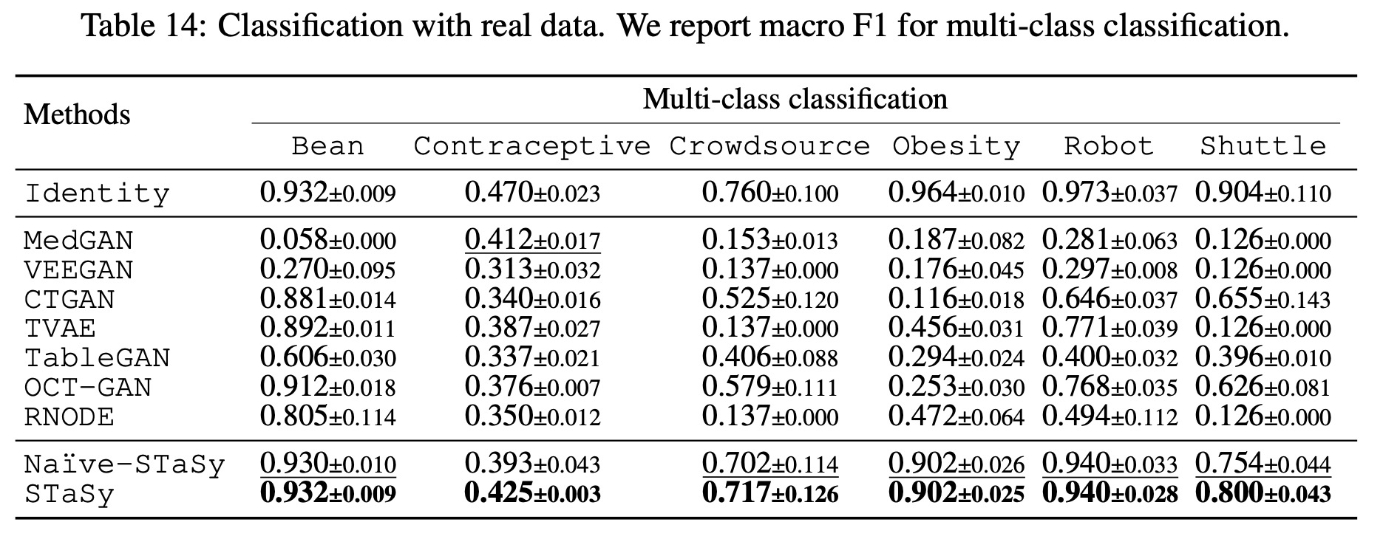
Crowdsource、Obesity、Robotといったデータでは他の手法を圧倒しています. このことについて, クラスごとのim-balancedが原因ではないかと考察されています.
このことは, 2値分類のCreditでも見られます. このデータは

Sampling Diversity
続いて, coverageを用いた多様性の比較をします.
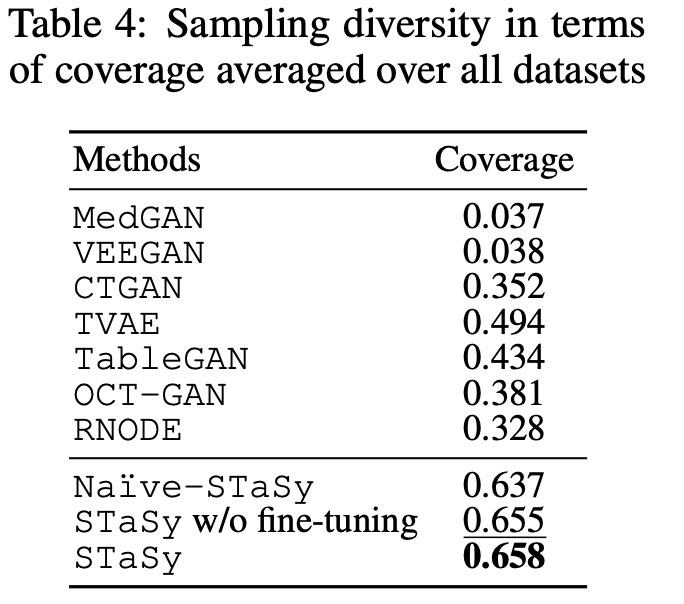
表からもわかるように, STaSyは非常に優れた結果を示しています. Robotデータをt-SNEで可視化した図を示します. 赤で囲まれた部分は特に実データとの分布の差が大きいことがわかります.

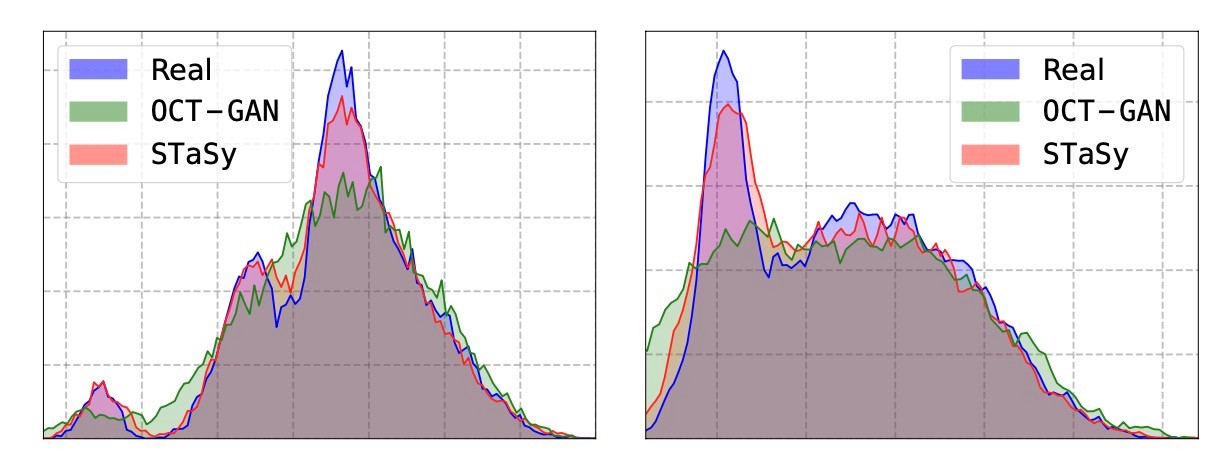
続いてBeanデータのRoundness (左)とCompactness (右)カラムのヒストグラムをみます. 多様性のために提案されたOCT-GANですが, 実データの分布を大きく外していることがわかります. それに対して提案手法はより詳細に分布をとらえていることがわかります.
Sampling Time
続いて, 生成速度を比較します. 訓練データと同じ量生成するために要した時間を比較しています. 全てのデータの平均を示していますが, 個々のデータで訓練データのサイズに違いがあるのであまり比較できないような気がします. 例えば, Creditは264.8Kですが, Contraceptiveは1.2Kです. 著者らはquality, diversity, speedのトレードオフがバランスよく取れていると主張していますが, それはどうなのでしょうか. TVAEと比較してみると100倍の時間がかかっていますがそれに見合った品質と多様性かは主観的な判断な気がします.

Ablation Study
ここでは, fine-tuning&SPLなし, fine-tuningなし, SPLなし, STaSyとの比較をして手法の要素が有用であることを示します.

概ね要素を追加していくと品質が上昇していることがわかります. 特にSPLは多様性に貢献します. Beijingの生成例を可視化すると, SPLを行ったことで多様性が生まれていることが確認できます. 特に, SPL無しではややモード崩壊が見られます (赤で囲まれた部分). 確かに, 図ではSPLなしでモード崩壊が確認できます. しかし, これがcherry pickingであることを否定できないのでcoverageで出すべきだと思いました.

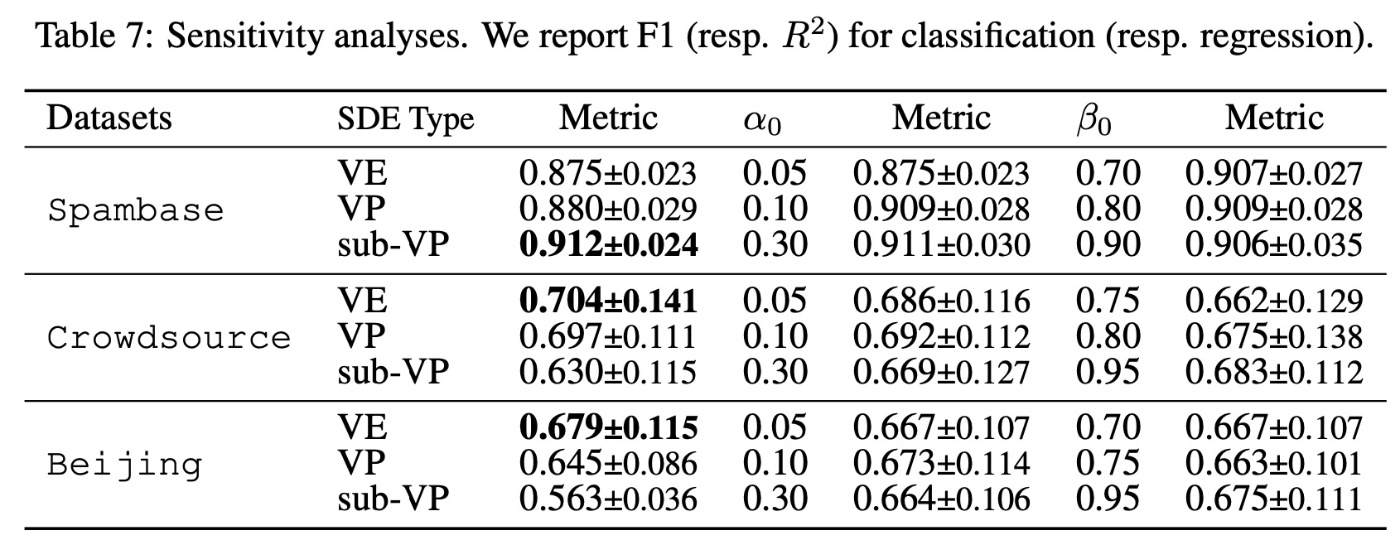
Sensitive Study
提案手法では一般的なハイパーパラメータ以外にも, 様々な設定要素がありました. 例えば
いくつかのパラメータを変更して実験した結果が以下の表です. 基本的にどの設定でも性能が高いです. 著者らは
まとめ
- スコアベースの表データ生成モデルの提案
- 提案手法は3つの大きな特徴がある
- スコアベースのモデル
- self-paced learning
- fine-tuning approach
- 15のデータセットと7つのベースラインを用いた比較ではqualityとdiversityで既存手法を凌駕
思ったこと
- 最新のスコアベースの手法を取り入れていて, かつパフォーマンスも良い
- 定量的指標がに加えて可視化された図も多く, 説得力がある
- OpenReviewの査読に対する反論が全くないのが気になる
- CoDiの際にも思ったことであるが, speedがよくないのでgenerative trilemmaを持ち出すのはやめた方がいいように思う (査読者の1人もruntimeがmajor concernと述べています)
参考文献
- Kim, J., Lee, C., and Park, N. STasy: Score-based tabular data synthesis. In The Eleventh International Conference on Learning Representations, 2023. (https://openreview.net/forum?id=1mNssCWt_v)
Discussion