Stable Diffusionからの概念消去④:SalUn (論文)
SalUn: Empowering Machine Unlearning via Gradient-based Weight Saliency in Both Image Classification and Generation (ICLR2024)
今回はMachine Unlearning (MU)の手法であるSalUnを見ていきます. これまでの概念消去もMachine Unlearningにカテゴライズされますが, 主にtext-to-imageに焦点が当たっていました. 今回の手法はそれを飛び越えて画像生成と画像分類を対象に研究をしています.
図や表はことわりのない限り論文からの引用になります.
書籍情報
Chongyu Fan, Jiancheng Liu, Yihua Zhang, Eric Wong, Dennis Wei, Sijia Liu. SalUn: Empowering Machine Unlearning via Gradient-based Weight Saliency in Both Image Classification and Generation. The Twelfth International Conference on Learning Representations, 2024
関連リンク
TL;DR
この論文で著者らは, 1つのQuestionを掲げています.
Is there a principled approach for effective MU in both classification and generation tasks?
この問いを扱ったものが提案手法のSalUnですが, 著者らは以下の4つの貢献を述べています.
- 既存のMachine Unlearning手法の問題点を2つ指摘した (汎用性の欠如と不安定性)
- saliency mapを用いて更新する重みと更新しない重みを分けてUnlearningする手法であるSalUnの提案
- 画像分類と画像生成でどちらも既存手法を上回る結果
- 注目すべき応用例として, I2P (不適切なプロンプト)が与えられたときに安定した有害な画像の生成を既存手法より多く防ぐことができる
論文に掲載されている手法の比較を見てみます. 従来のMU手法は更新するパラメータを事前に決めて行います. それにもかかわらず能力はマチマチで概念消去がうまくいかないこともあります. それに対してSalUnでは, maskのようなものを用意してunlearningの状況に応じて更新するパラメータを選びます. さらに能力が高いというのが著者らの主張です.
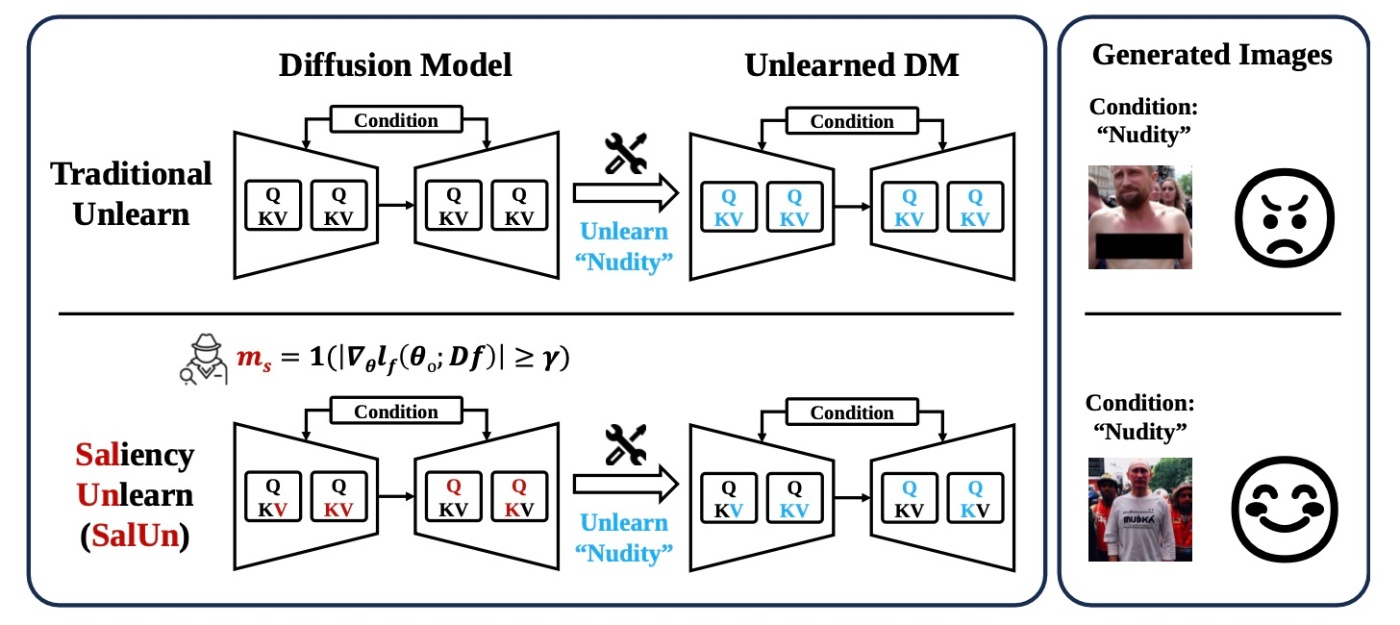
問題設定
問題設定をするための準備と, 問題設定をします.
RetrainはMUのgold standardです. すなわち, 何かを忘れさせるときはその対象のデータセットを取り除いたデータセット
これは,
以降では, 画像分類と画像生成に焦点を絞って, それぞれの既存手法をさらっと見ます.
画像分類
画像分類におけるMUは
- クラス別の忘却
- ランダムなデータの忘却
また, それらの評価指標として, 統一的な指標はないものの, ここではfull stack metricsに従うことにします. これは複数の指標を併用して評価を行うもので, 具体的には以下の5つです.
- unlearning accuracy (UA):
\boldsymbol{\theta}_{\mathrm{u}} \mathcal{D}_{\mathrm{f}} 1-\mathrm{accuracy} - membership inference attack (MIA):
\mathcal{D}_{\mathrm{f}} \boldsymbol{\theta}_{\mathrm{u}} - remaining accuracy (RA):
\mathcal{D}_{\mathrm{r}} \boldsymbol{\theta}_{\mathrm{u}} - testing accuracy (TA):
\boldsymbol{\theta}_{\mathrm{u}} - run-time efficiency (RTE): Unlearnするのに必要な時間です.
画像生成
ここでは条件付き拡散モデルによる生成を考えます. ただの条件なのでtext-to-imageには限定されないです. 例えばクラス指定生成やレイアウト指定も可能です. 拡散モデルそのものについては主題ではないので詳しく取り扱いませんが, 一般的な記法を用いると以下の以下のMSE lossを用いて学習します.
十分に訓練された拡散モデル
- 有害な概念が条件として与えられたときに望まない生成をしないよう
\boldsymbol{\theta} - 生成品質を維持しながら
\boldsymbol{\theta}
これらの手法は, 当初はMUの枠組みでは議論されていませんでした. 特に, "learning to forget"や"concept erasing"などと呼ばれています. この論文ではMUを通してその枠組みを構築することを目指します.
現在のMUの限界
提案手法に入る前に, 現在のMUではどのような限界があるかを確認します. 著者らは2つの欠点を指摘しています.
- unlarningの安定性
- 汎用性の欠如
この欠点を確認するために, まずは既存の5つの手法を再検討しています.
- Fine-Tuning (FT):
\boldsymbol{\theta}_{\mathrm{O}} \mathcal{D}_{\mathrm{r}} - random labeling (RL): random labelを用いて
\mathcal{D}_{\mathrm{f}} \boldsymbol{\theta}_{\mathrm{O}} - gradient ascent (GA): 勾配上昇を利用する. 通常の学習では勾配降下法を用いて学習しますが, 反対方向に学習することで忘れることができます.
- influence unlearning (IU): 影響関数を用いて
\mathcal{D}_{\mathrm{f}} \boldsymbol{\theta}_{\mathrm{O}} -
\ell_1
安定性の欠如
既存研究では
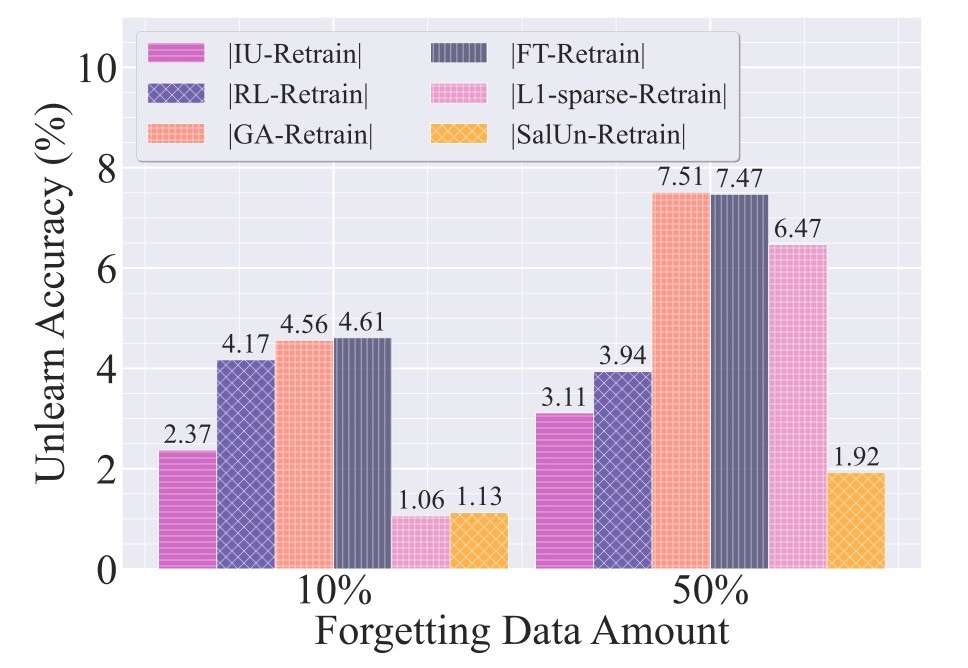
UA (unlearning accuracy)を見てみると, 既存手法は
続いて, ハイパーパラメータの変化に対する性能比較を行います.

IU(influence unlearning)を例にとると, Fisher情報正則化パラメータの調整が必要になります. CIFAR-10の10%を忘れさせるとき, IUはRetrainに比べてUAが非常に大きい分散となります. しかし, 提案手法はその分散を小さくすることに成功しています. なお, Fisher情報正則化パラメータについては以下の2つの論文がこの論文では参照されています.
汎用性の欠如
本研究の目的は画像分類と画像生成のどちらにも適用可能な方法の提案にあります. そのためには既存手法が画像生成に適用可能かを調べる必要があります. CIFAR-10を用いてairplaneを忘れさせる実験を行います.
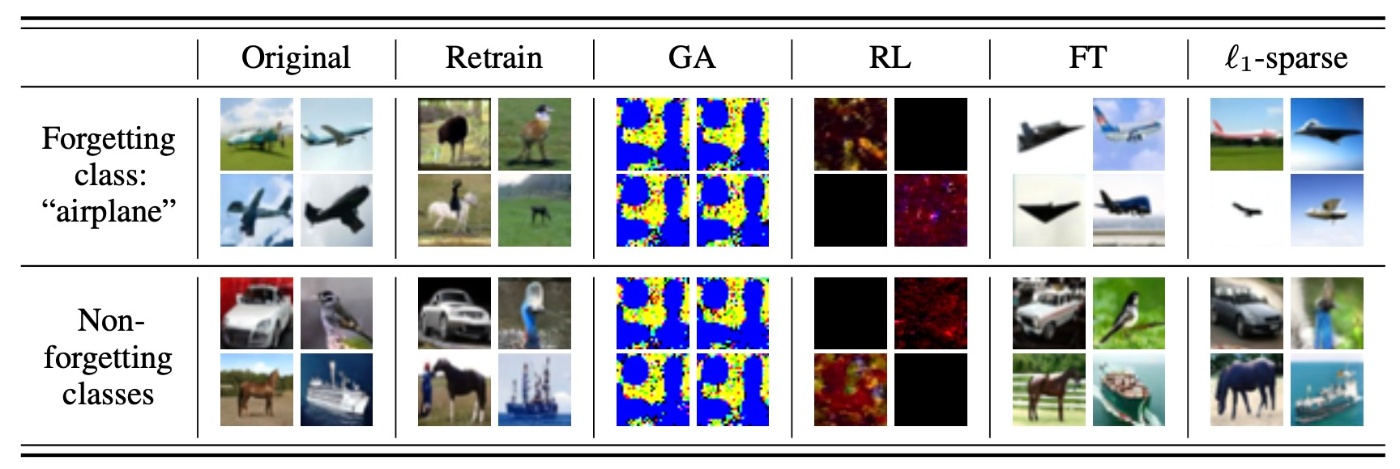
結果を見てみると, GAとRLでは
SalUn: Weight Scaling is Possibility All You Need for MU
既存手法の問題点などを確認したので提案手法に移ります. 大言壮語なセクション名ですが, これは論文のセクション名をそのまま使っています. 個人的にはPossibilityというワードを使うならAll You Needと言うなと思うのですが, それは別の話です.
提案手法は, weight saliencyという概念を導入し, saliency-guidedアプローチを用いています.
まずはなぜこのアプローチであるのかという部分が説明されています.
著者らはまず, 以下の論文に着目しました.
この論文は, 機械学習モデルがある程度のモジュラリティを有していることを示唆するものです. ここで言うモジュラリティとは, 大規模な機械学習モデルが管理しやすい部分に分解され, それぞれがより独立して維持および更新できる特性を指します.
モジュラリティの重要な要因として考えられているものに重みのスパース性があります. これはモデルの効率性, 解釈可能性, 堅牢性などの改善に寄与しているものです. MUの文脈では, unlearning processを促進するものとして活用されています. ただし, MUに適用する際に重みのスパース性にはいくつかの制限があります.
- モデルの適切なスパースパターンを決定すること自体が難しい場合がある
- 実現可能でもスパース化したモデルは性能が低下する可能性があり, 応用上適切でない
そこで, スパース化するのとは異なる解決方法を探ります. 勾配ベースのsaliency mapをヒントに, saliency mapを用いたMU手法を考えます. これによって, MUで更新される重みとされない重みに分解できます. input saliency mapと同様に, 忘却関数
この式に従うと,
既存のMUで用いられている忘却関数は
- 画像分類
- 画像生成
CEはcross entropy lossです.
ようやく提案手法SalUnに入ります. これは先ほどのsaliency mapを用いた重み更新を取り入れたプロセスです. 大きな特徴は, 既存手法と組み合わせて用いることができる点にあります. 例えば画像分類ではRL (random labeling)との組み合わせが有効だそうです. すると, 以下の最適化問題に帰着されます.
これに加えて汎化能力を維持するためoriginal modelを上の式を用いて微笑せいします.
続いて, 画像生成に適用します. 画像分類と同様にRLを使用します. 概念
実験
かなり手法のパートが長かった気がしますが, 実験を通して有効性を確認します. 実験設定のあと, 結果を確認します.
実験設定
まずはデータセットなどを見ます.
-
画像分類:
先ほど同様RLと併用します. ベースとなるモデルはResNet-18をCIFAR-10で訓練させたものです. これに加えてCIFAR-100, SVHN, Tiny ImageNetでも実験を行います. これらのデータセットではVGG-16, Swin-Tを訓練します. -
画像生成:
クラスの忘却 (DDPM)と概念の忘却 (Stable Diffusion)の2つを実験します. クラス忘却ではCIFAR-10を用います. この設定はImagenette datasetを用いてStable Diffusionでも行います. 概念の忘却はNSFWの生成阻止を目標に行います.
続いて, ベースラインと評価指標を確認します. 基本のベースラインは以前に確認した以下の5つです.
- Fine-Tuning (FT)
- random labeling (RL)
- gradient ascent (GA)
- influence unlearning (IU)
-
\ell_1
それに加えて, 2つのboundary unlearning methodsを画像分類では用います.
- boundary shrink (BS)
- boundary expanding (BE)
画像生成でも2つの手法をベースラインとして用います.
- erased stable diffusion (ESD)
- forget-me-not (FMN)
評価指標も以前確認した5つのものを用います.
- unlearning accuracy (UA)
- membership inference attack (MIA)
- remaining accuracy (RA)
- testing accuracy (TA)
- run-time efficiency (RTE)
画像生成ではUAとして分類器を別に訓練して計測します. CIFAR-10で訓練したResNet-34とImageNetで訓練したResNet-50を用います. それに加えてFIDを使用します.
実験結果
では, 結果を確認します. まずは画像分類です.

SalUn-softとは, 閾値
以前
- 両方の設定でRetrainとのAvg. Gapが最小である. 特に, SalUn-softはSalUnと比較したときにMIAが悪い.
厳密なスパース性を持つ重みのsaliency mapがMUの効果的性能に利益をもたらす一方で, SalUn-softではスパース性が厳密に強制されない可能性があるので結果が悪いと考えられます. このことから, 以下ではSalUn-softは言及しないことにします.
- 1つの評価指標ではMU手法を十分に評価できていない.
これはMUに限らず様々なところで言われる現象です. 評価指標はハックされるものですし, できるだけ多くの評価指標を採用して全体的な話をしなければなりません.
-
|\mathcal{D}_{\mathrm{f}}|=|\mathcal{D}_{\mathrm{r}}|
これは単純に難しいタスクであることを表します. 著者らは10%の場合で競合するBSと
続いて, 画像生成の結果を確認します. まずはクラス生成です.

saliency mapで重みをmaskをするわけですが, それをrandom maskingと比較することでSalUnの有効性を確認します. random maskingではairplaneでは意味のない生成になったり, C2やC3などは何が生成されているのか不明瞭です. 特に, 忘却させたクラスではretrainの結果とは異なります (と主張していますがretrainの結果が示されていないのでわからないです). 少なくとも
続いて, 下流タスクでの結果を確認します.
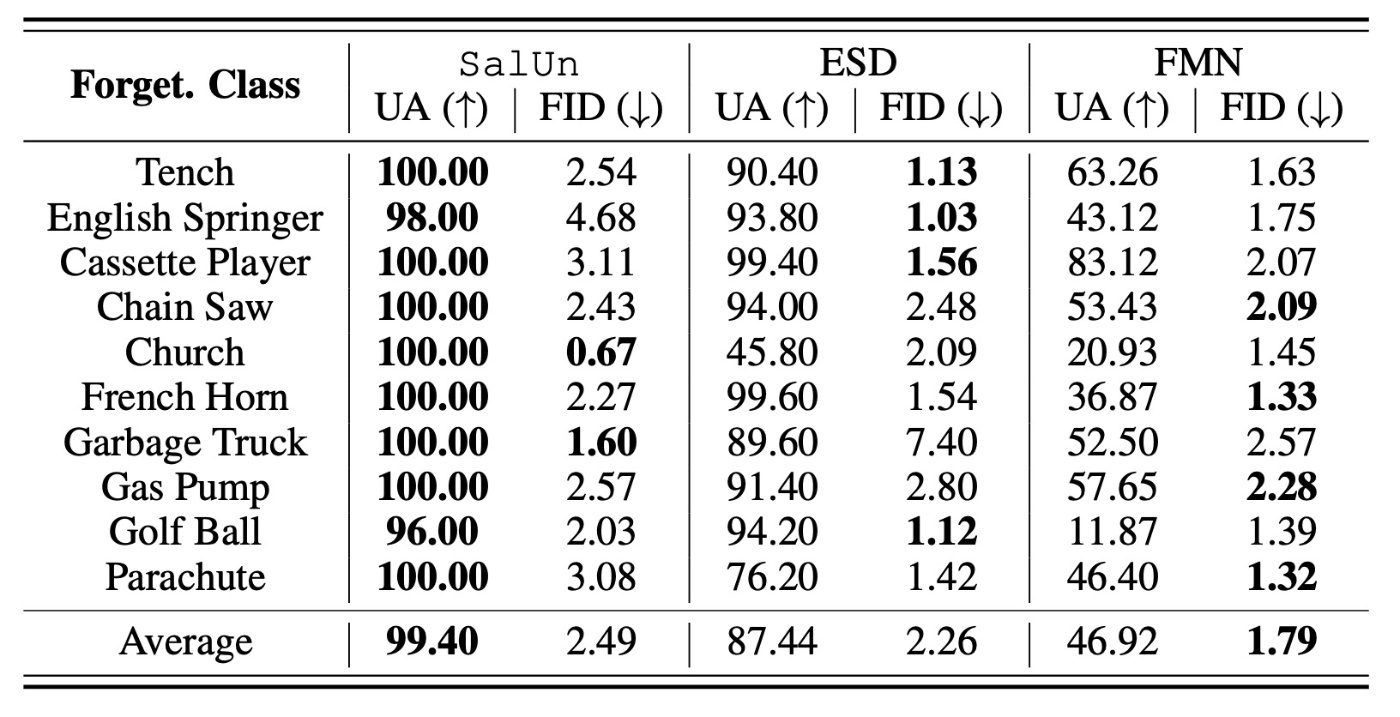
FIDではSalUnは全く歯が立ちませんが, UAでは圧勝しています. 特に, ESDなどでは難しかったChurchでも圧倒的な性能を示しています. 他のクラス画像に割り当てる学習をしているので当然だろうという感じですが, そうなると同じような手法のconcept ablationやUECとの比較が欲しいです.
2つの指標を併用すると, 低いFIDで高いUAであるSalUnが優れているという結論になりそうです.
続いて, NSFWの結果を確認します.
まずは, I2Pを用いた際の生成数を比較します. NudeNetで検出しています.
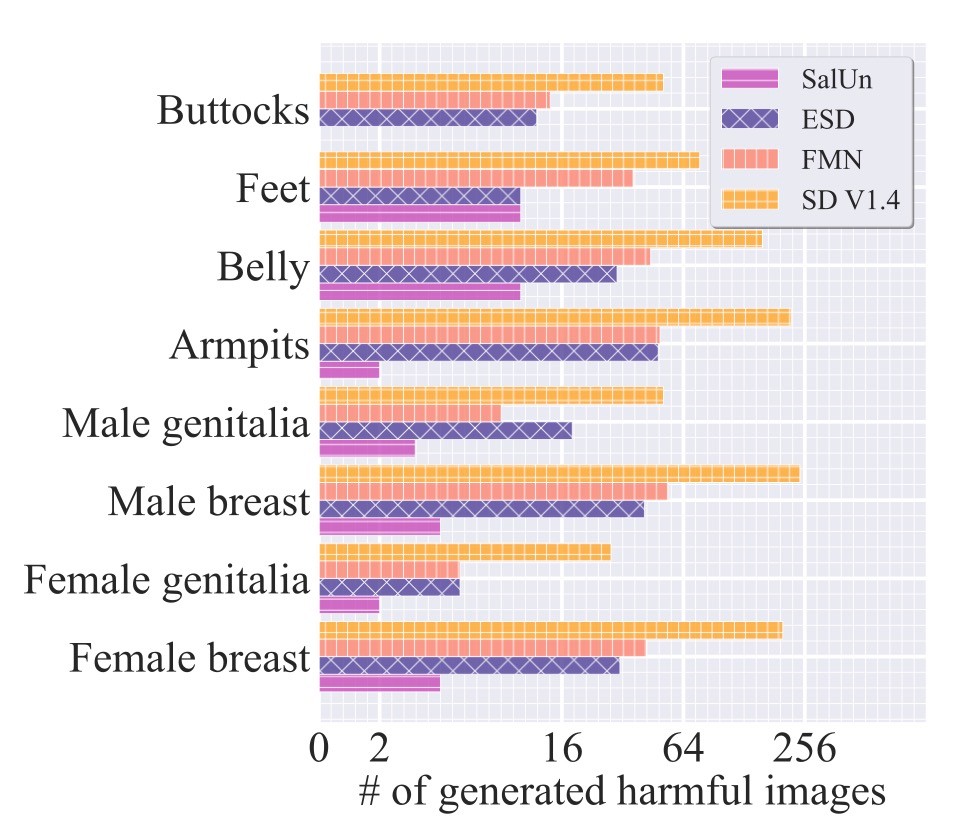
横軸が対数グラフであること考慮すると, 提案手法は非常に優れた結果を残していると考えられます.
論文では続いて生成例を確認しています. 著者によって黒塗りされているとはいえ性的コンテンツですので省略します. 論文ではFigure 6のものです. 定性的にみてもSalUnは黒塗り部分がなく, 高い精度での忘却が可能であることがわかります.
まとめ
- 画像分類と画像生成のmachine unlearning手法を統一的に扱う手法の提案
- saleincy mapという重みに注意を向けたmapを用いることで性能が上昇
思ったこと
- 画像生成での実行時間比較がなかったのは気になります.
- 画像生成の下流タスク性能比較はclip accuracyが既存研究で用いられていましたが, なぜこれを変更したかの説明はありませんでした.
- 既存のMU手法を全てベースラインに用いるなど, かなり実験量がすごそうだと思いました.
- saleincy mapを用いて動的に更新パラメータを決めるのは賢いなと思いました. 通常だとLoRAなどで代替してしまいそうです.
- 概念消去の文脈でよく見るどれくらい消せるかという議論はありませんでした. 画像分類では確認しましたが, この研究の趣旨から考えるとあって然るべきに思えます.
参考文献
- Chongyu Fan, Jiancheng Liu, Yihua Zhang, Eric Wong, Dennis Wei, Sijia Liu. SalUn: Empowering Machine Unlearning via Gradient-based Weight Saliency in Both Image Classification and Generation. The Twelfth International Conference on Learning Representations, 2024



Discussion