Unified Concept Editing in Diffusion Models (WACV2024)
今回は閉形式を用いることで概念消去を行えるUCEという手法を見ていきます. 今回は少し数式の話が多いですが, 大学1年生程度の線形代数の知識があれば十分です.
図や表はことわりのない限り論文からの引用です.
書籍情報
Rohit Gandikota, Hadas Orgad, Yonatan Belinkov, Joanna Materzyńska, David Bau. "Unified Concept Editing in Diffusion Models." IEEE/CVF Winter Conference on Applications of Computer Vision (WACV) 2024.
関連リンク
TL;DR
- 閉形式で概念を消去する手法の提案
- cross attentionの重みを更新
- バイアスなどを軽減することも可能
前提
手法に入る前に, 拡散モデルの条件付けや既存手法の部分を確認します. 用いている記号は論文のものに従っています.
拡散モデルそのものの説明は省略しますが, 一般的な記法を用いるとdenoisingは以下のように記述できます.
p_\theta(x_{T:0})=p(x_T)\prod_{t=T}^1p_\theta(x_{t-1}|x_t)
text-to-image diffusion modelsの場合はテキストを条件に与えます. テキストはtext embeddingに埋め込まれ, それが条件となります. text embedding c_i が与えられたとき, 条件付けに用いるattentionモジュールのうちkeyとvalueはそれぞれ k_i=W_kc_i, v_i=W_vc_i で計算されます. Attention Mapsはクエリ q_i と合わせて
\mathcal{A}\propto\mathrm{softmax}(q_kk_i^T)
となります. これを用いてcross attentionの出力は
\mathcal{O}=\mathcal{A}v_i
です.
さて, TIMEという既存手法があります.
https://openaccess.thecvf.com/content/ICCV2023/html/Orgad_Editing_Implicit_Assumptions_in_Text-to-Image_Diffusion_Models_ICCV_2023_paper.html
この手法も本論文と似たアプローチでtext-to-image diffusion modelsの前提知識 (オブジェクトの視覚的特徴)の編集を行います. 例えば, 「バラは赤色である」といった知識や「医者は男性が多い」というバイアスなどといったものです (これらのバイアスは多くの場合訓練データに依存しますが, 基本的に訓練データは膨大なので人間がチェックすることが難しいです. もちろんやっているところもあると思います). TIMEの手法は W_k と W_v を更新して埋め込み表現を変更することで実現されます. c_i をsource promptの埋め込み, c_i^* を目的プロンプトの埋め込みとします. このとき, v_i^*=W^{\mathrm{old}}c_i^* です. 新しい重み行列は次の式を最適化して得ることができます.
\min_{W}\sum_{i=0}^m\|Wc_i-v_i^*\|_2^2+\lambda\|W-W^{\mathrm{old}}\|_F^2
この式は次のように閉形式で書けます.
W=\left(\sum_{i=0}^mv_i^*c_i^T+\lambda W^{\mathrm{old}}\right)\left(\sum_{i=0}^mc_ic_i^T+\lambda\mathbb{I}\right)^{-1}
ここで \displaystyle\sum_{i=0}^mc_ic_i^T は編集される概念テキスト埋め込みの共分散です. また, 第2項の単位行列は拡散モデルの語彙に含まれる大規模な概念埋め込みの共分散に対応するものと解釈されます.
手法
では, 手法についてみていきます. 事前学習された重み W^{\mathrm{old}} が与えられたとき, 下図にあるように集合 E 内の一連の概念を編集し, 同時に集合 P 内の概念を保存する新しい編集された重み W を見つけることが目標です.
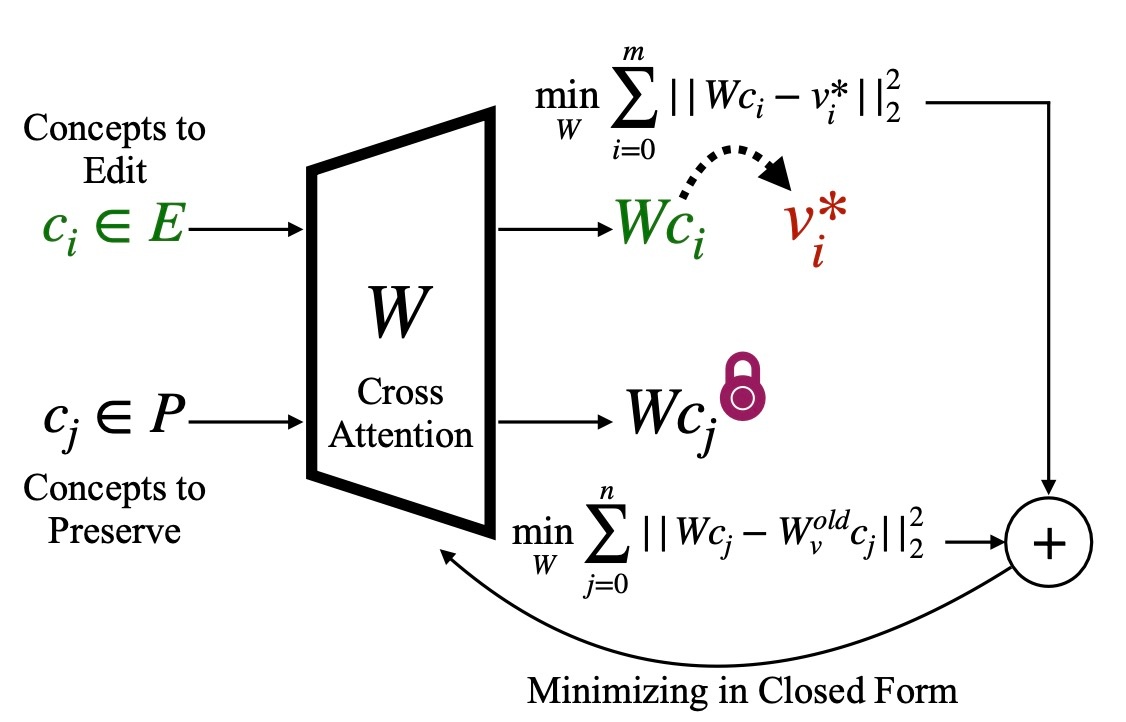
具体的には, 各入力 c_i \in E に対する出力が、元の W^{\mathrm{old}}c_i に対応する出力ではなく, v^* = W^{\mathrm{old}}c^* にマップされるような重みを見つけたいです. 同時に, 入力 c_j \in P に対応する出力は W^{\mathrm{old}}c_j として保存されます. すると, 目的関数は次のようになります.
\min_{W}\sum_{c_i\in E}\|Wc_i-v_i^*\|_2^2+\sum_{c_j\in P}\|Wc_j-W_v^{\mathrm{old}}c_j\|_2^2
これはTIMEの目的関数と似ているので, 閉形式で書けそうな雰囲気があります. この式を W で微分し, それを0とすると,
\begin{align*}
&\sum_{c_i\in E}2(Wc_i-v_i^*)c_i^T+\sum_{c_j\in P}2(Wc_j-W_v^{\mathrm{old}}c_j)c_j^T=0 \\
&\sum_{c_i\in E}Wc_ic_i^T-\sum_{c_i\in E}v_i^*c_i^T+\sum_{c_j\in P}Wc_jc_j^T-\sum_{c_j\in P}W_v^{\mathrm{old}}c_jc_j^T=0 \\ \\
&\sum_{c_i\in E}Wc_ic_i^T+\sum_{c_j\in P}Wc_jc_j^T=\sum_{c_i\in E}v_i^*c_i^T+\sum_{c_j\in P}W_v^{\mathrm{old}}c_jc_j^T \\ \\
& W\left(\sum_{c_i\in E}c_ic_i^T+\sum_{c_j\in P}c_jc_j^T\right)=\left(\sum_{c_i\in E}v_i^*c_i^T+\sum_{c_j\in P}W_v^{\mathrm{old}}c_jc_j^T\right)
\end{align*}
左辺の \displaystyle\sum_{c_i\in E}c_ic_i^T+\sum_{c_j\in P}c_jc_j^T が逆行列を持てば W= の形で書けます. 行列 A が逆行列を持つとき A は正則行列ですが, これは A がfull rankであることと同値です. そのため, \displaystyle\sum_{c_i\in E}c_ic_i^T+\sum_{c_j\in P}c_jc_j^T はfull rankである必要があります. ここで, 保存項を追加してrankを1以上増やします. これは, 行列のrankの性質
rank(A+B) \leq rank(A) + rank(B)
から従います. rank(X)=0 \Leftrightarrow X=O だからです. すると, 保存項の数 |P| がtext embeddingの次元 d より小さい場合 (|P|<d) ,full rankにならない可能性があります. そのため, text embeddingの基底方向に沿った d 個の追加の保存項を導入します. これによってfull rankが保証され,
W=\left(\sum_{c_i\in E}v_i^*c_i^T+\sum_{c_j\in P}W_v^{\mathrm{old}}c_jc_j^T\right)\left(\sum_{c_i\in E}c_ic_i^T+\sum_{c_j\in P}c_jc_j^T\right)^{-1}
となり, 閉形式で書けました. 形式的な保存項を追加することで, P のサイズに関係なくfull rankを維持することができます. keyも同様に最適化できます.
これはTIMEやMENITの一般化になります. MENITについては扱わず, ここではTIMEの一般化であることだけを示します.
TIMEの一般化の証明
UCEの閉形式において, P を指定しない状態を考えます. また, 形式的に追加する基底を \lambda だけスケーリングさせても問題ないです.
W=\left(\sum_{c_i\in E}v_i^*c_i^T+\lambda\sum_{j=0}^dW_v^{\mathrm{old}}e_je_j^T\right)\left(\sum_{c_i\in E}c_ic_i^T+\lambda\sum_{j=0}^de_je_j^T\right)^{-1}
ここで, 和 \sum_{j=0}^de_je_j^T について考えます. e_j はj 番目の要素のみ1で他は0の対角行列である外積 e_je_j^T を持ちます. そのため和 \sum_{j=0}^de_je_j^T は単位行列に等しく
W=\left(\sum_{c_i\in E}v_i^*c_i^T+\lambda W_v^{\mathrm{old}}\mathbb{I}\right)\left(\sum_{c_i\in E}c_ic_i^T+\lambda\mathbb{I}\right)^{-1}
です. これは先ほど確認したTIMEの式であることがわかります. すなわちUCEはTIMEに保存する概念を追加したより一般化された表現であることがわかります.
提案手法は W_k と W_v を編集して, 異なる目標を持つさまざまな概念の編集を行います. ここでは概念の消去, 緩和, およびバイアスの除去です. この手法は m 個のtext embedding c_i とそれらの編集対象の修正されたtarget output v_i^∗ に由来する概念のテキストの説明が必要です. 編集タイプに基づいてtarget outputは異なる方法で定義されます (後述). また, 周囲の概念を n 個保持し, それらの説明で c_j を使用します。複数のトークンを持つ概念の場合, c_i の最後のトークンを v_i^∗ の最後のトークンに整列させて編集を行います.
では, target outputの定義をみていきます.
Erasing
概念 c_i を消すときは, それが生成されないようにしたいです. 例としてKelly Mckernan styleの消去を考えます. このときは target output v_i を別の概念 c_* (ここではart)でアラインメントします.
v_i^*\leftarrow W^{\mathrm{old}}c_*
これにより, 出力が概念 c_i を反映しないように重みが更新されて, 概念の消去が実現します.
Debiasing
特定の概念 c_i のバイアスを消すときは, その概念に付随する属性が生成されにくくなるようにしたいです. 例えばdoctorを c_i とし, それに付随する属性 a_1, a_2, \ldots, a_p をwhite, asian, black...などとします. これは属性のプロンプトに対応する v_{a_1}, \ldots, v_{a_p} の大きさを調整することで得られます. ここで, v_{a_i}=W^{\mathrm{old}}a_i です.
v_i^*\leftarrow W^{\mathrm{old}}[c_i+\alpha_1a_1+\alpha_2+a_2+\cdots\alpha_p a_p]
定数 \alpha_i はどの程度属性を生成するかを表す定数で, TIMEといった既存の手法ではできなかった属性ごとのバイアス低減が実現できます.
Moderation
これは, Erasingとほとんど同じです. ただし, c_* を空文字列とします.
実験
まず, Erasingの結果をみてみます. 比較手法はESD-x, Concept Ablation, SDD (Safe self-Distillation Diffusion)です.
Artist Erasure
styleの結果をみてみます. 提案手法とESD-x-1は多くのstyleの消去能力があります. SDDとAblationはあまり多くの概念を消せないようです.

他の概念への影響を確認します. 提案手法とSDDは他の概念への影響が少ないです. 一方でAblationとESD-x-1は他の概念への影響が大きいです. このことはCLIP ScoreやLPIPSのグラフをみてもわかります. LPIPSは1番低く, CLIP Scoreは1番高いです. CLIP Scoreを見てみると, 提案手法とSDDは一度下がったスコアが上昇していますが, この原因については触れられていませんでした.
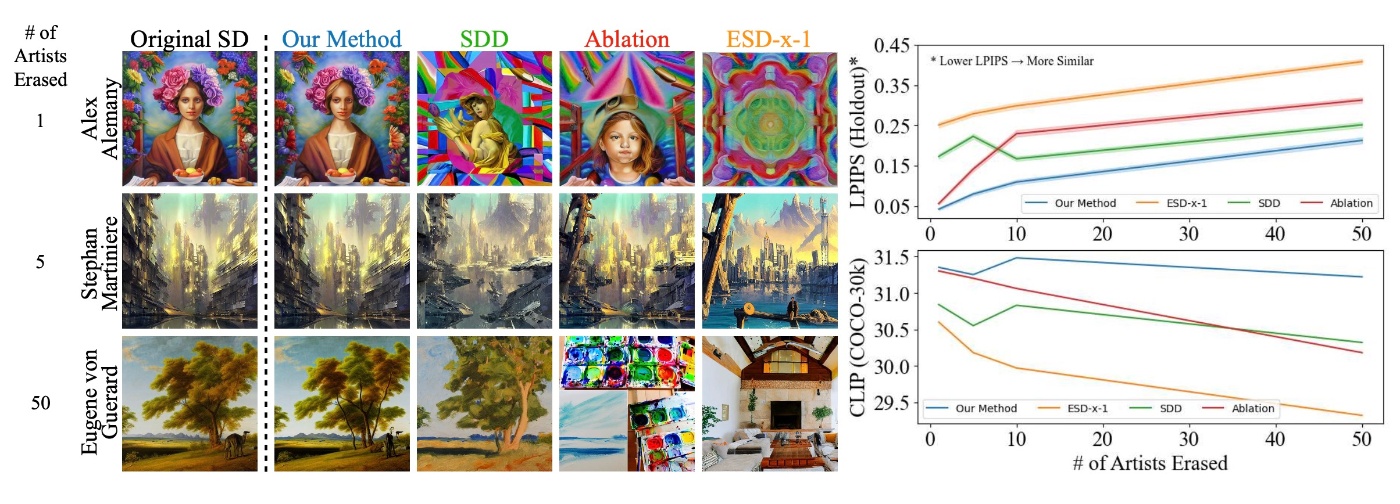
これらのことから, 他の概念の影響を最小限にしつつ, 提案手法は多くの概念を消すことができることがわかります.
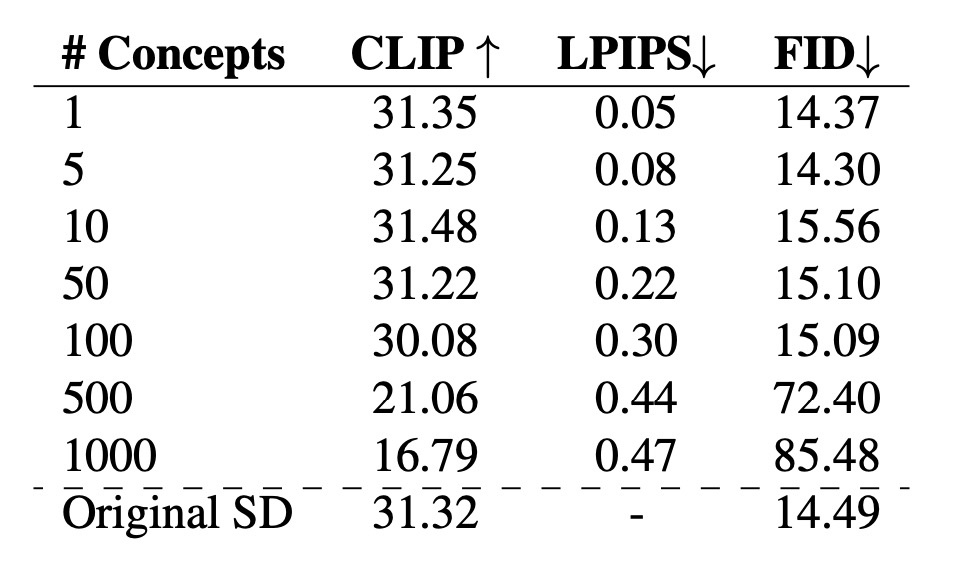
しかし, 効果的に消せる概念は100程度です. 下の表の通り, 100から500になると各種スコアが悪化します. また, 50を超えると他の概念の維持は難しくなるようです. スコアには現れていませんが, 生成画像がOriginal SDのものとは異なると述べられています.
Erasing Object
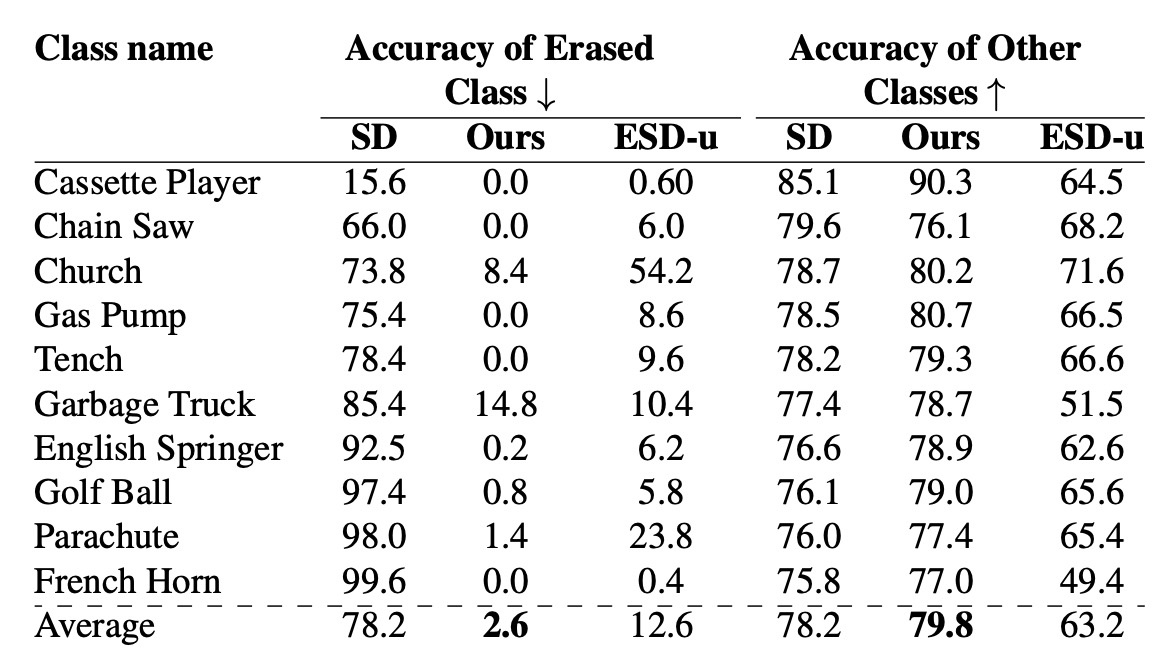
オブジェクトが消せることを確認するため, ImageNetのsubsetであるImagenetteを用います. c_i として各種text embeddingを用います (例えば French Horn). 保存する概念 c_j は指定しません. 各クラス500枚の画像を生成し, 学習済みResNet-50でtop-1 accuracyを確認します. ここで, それぞれの概念につき1つのモデルが用意されています. 結果を確認すると, 消した概念については分類モデルの正答率が下がっています. ESD-uとの比較では大幅に改善されていることがわかります. しかし, Garbeage Truckでは分類精度が高くなっています. このことについては言及がありません. 他の概念の正答率はESD-uよりいいですが, Original SDより精度が上昇している点も言及がありませんでした.
Debiasing
定数 \alpha を動的に変更しつつ, バイアスの低減を行います. まずはgender biasの解消結果を見ます.

Original SDでは男性あるいは女性に偏っていた生成例に, 多様性ができたように見えます. このことは定量的にも示されています (結果は省略します).
続いて, racial biasの解消結果を確認します. アメリカの行政予算管理局 (OMB)が指定した人種カテゴリを目標とします. 具体的には「白人, 黒人, アメリカインディアン, ネイティブアメリカン, アジア人」です. 画像から人種を分類するタスクは既存のモデルや人間の結果は非常にバイアスがかかっているために定量的比較が困難です. そのため, 定性的な比較のみを行います. 結果として, 多様な人種が生成されているように見えます.

Moderation
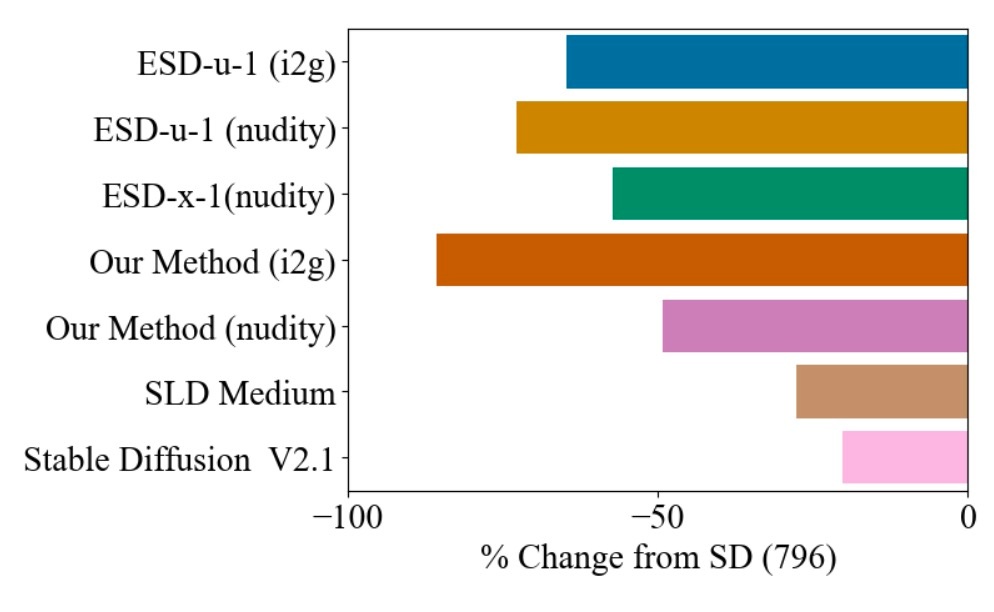
I2P promptで生成された4703枚の画像に対してNudeNet classifierで分類した結果を示します. 同じcross attentionを更新するESD-x-1と同等の性能を示しています. golbalに消去を行うESD-u-1の方がより期待した成果を得ることができます.
まとめ
- 閉形式で概念を消去する手法の提案
- cross attentionの重みを更新
- バイアスなどを属性ごとに軽減することも可能
思ったこと
- 論文を見ると表記揺れがやや見られます. 査読者は見落としたのでしょうか. それとも全員がAppendixを読まなかったのでしょうか.
- TIMEの一般化であるという証明もやや強引だと思います. それはUCEには \lambda が登場していないので \lambda=1 の場合としか見なせないからです. 数学の論文は読んだことがないですが, これが普通なのでしょうか.
- この論文でもやはりOriginal SDの出力を正解とする根拠は触れられていないように見えます. Objectの消去の結果の表で見た通り, Accuracy of other classesはOriginal SDと比較して上昇しています. これはOriginal SDの出力をしていない可能性がありますが, 論文内ではその定性的比較はされていません.
- 閉形式で書けることはそれなりにメリットだと思います. しかし, P や \boldsymbol{c}^* の選び方に左右されると思うので, ちゃんと書いて欲しいなと思いますしその差による結果の比較も欲しいと思います.
- 一方で, バイアス解消とモデレーション, 概念消去を同じ定式化の上で議論しているのはとてもいいと思いました. 今は他の概念を外から指定していますが, これが暗黙的にできるととても嬉しいです.
参考文献
- Rohit Gandikota, Hadas Orgad, Yonatan Belinkov, Joanna Materzyńska, David Bau. "Unified Concept Editing in Diffusion Models." IEEE/CVF Winter Conference on Applications of Computer Vision (WACV) 2024.
- Hadas Orgad, Bahjat Kawar, and Yonatan Belinkov. Editing implicit assumptions in text-to-image diffusion models. In Proceedings of the 2023 IEEE International Conference on Computer Vision, 2023.
- Kevin Meng,Arnab Sen Sharma, Alex J Andonian, Yonatan Belinkov, and David Bau. Mass-editing memory in a transformer. In The Eleventh International Conference on Learning Representations, 2023








Discussion