Zenn
🐕

Stable Diffusionからの概念消去⑥：SPM (論文)

2024/04/18に公開
機械学習
論文
Stable Diffusion
拡散モデル
tech

One-dimensional Adapter to Rule Them All: Concepts, Diffusion Models and Erasing Applications (CVPR2024)

今回はSPMという手法をみます. まだCVFでは論文が公開されていませんが, CVPR2024採択の論文です. ここではarXivのversion 1をベースに確認しますが, version 2と大きな違いがあるわけではなさそうです.

図や表はことわりのない限り論文からの引用です.

書籍情報

Lyu, M., Yang, Y., Hong, H., Chen, H., Jin, X., He, Y., Xue, H., Han, J., and Ding, G. One-dimensional adapter to rule them all: Concepts diffusion models and erasing ap- plications. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7559–7568, June 2024.

関連リンク

論文内にはプロジェクトページへのリンクが記載されていますが404です.

TL;DR

既存手法との比較を表したのが下の図です. 既存手法の主な問題点は

  • 消す概念が増えると対象でない概念も消失することがある
  • そのモデル単体で完結してしまい, 他のモデルに適用することができない

提案手法であるSPMはそれを解決します. SPMは "The concept-SemiPermeable structure is injected as a Membrane"のバクロニウム (的なもの？)です.

手法の核となる部分は以下の3つです.

  • 1-dim adapter
  • Latent Anchoring
  • Facilitated Transport

そして, PEFTベースでパラメータを更新するので取り外しが可能です.

手法

基本的にはpretrained modelsをfine-tuningするという既存手法を踏襲します. しかし, 普通にfine-tuningをしてしまうとparameter driftが発生してしまいます. そこで, 1-dim adapterを導入します. adapterですので, 取り外しができ, これにより転移が可能になります. その後, lantent anchoringによって正確な概念消去を可能にします. 最後に, 推論中の工夫としてfacilitated transportがあります.

手法の概要を表したものが下図です.

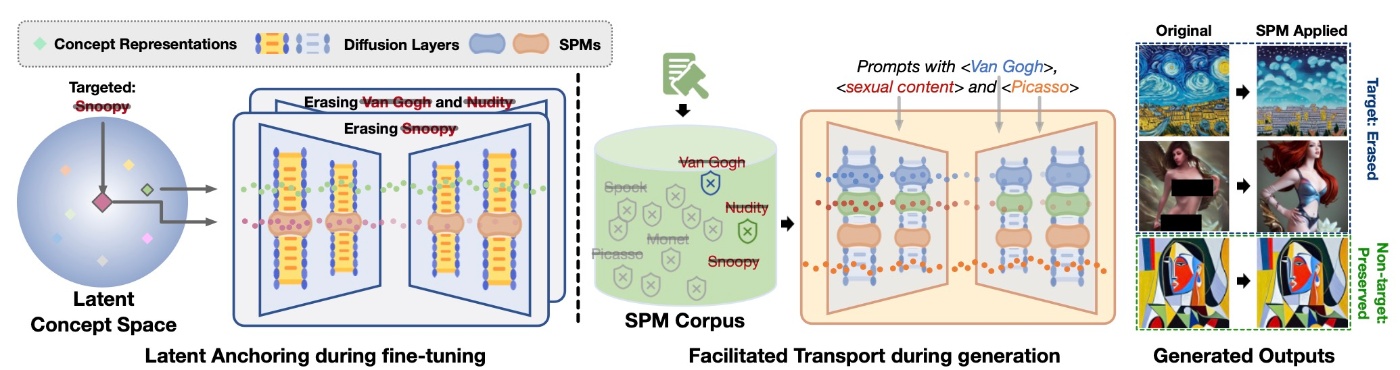
以降では順番に要素を確認します.

A 1-dim Lightweight Adapter

既存研究のfull parameter tuningは非常に効率が悪く, 先ほど触れたようにparameter driftがあります. そこで, PEFT (parameter efficient fine tuning)に触発された外付けのアダプターを用います. 固有次元は1で, 非常に軽量です.

数式的な部分を確認します. 拡散モデル内部のあるパラメータ \boldsymbol{W}\in\mathbb{R}^{m\times n} を考えます. 消去信号 \boldsymbol{v}_{sig}\in\mathbb{R}^m を学習することで概念消去を実現します. この信号の振幅は, 訓練可能なregulator \boldsymbol{v}_{reg}\in\mathbb{R}^n によって制御されます. これによって消去の度合いを決めることができます. 元々のforward processを y=\boldsymbol{Wx} と表すことにすると, SPMでは以下のようになります.

\boldsymbol{y}=\boldsymbol{Wx}+(\boldsymbol{v}_{reg}^T\boldsymbol{x})\cdot\boldsymbol{v}_{sig}

例として, LDM (Latent Diffusion Models)を考えてみます. LDMではテキストによる条件 c に基づいてノイズを予測します.

\hat{\varepsilon}=\varepsilon(x_t, c, t\mid\theta)

\theta はU-Netのパラメータを表します. これらの記号を用いるとSPMは \mathcal{M}_{c_{tar}}=\{(\boldsymbol{v}_{sig}^i,\boldsymbol{v}_{reg}^i)|c_{tar}\} のように定式化できます. これらは i 番目のレイヤーに挿入され, 概念 c_{tar} を消去します. すると, ノイズ予測は

\hat{\varepsilon}=\varepsilon(x_t, c, t\mid\theta, \mathcal{M}_{c_{tar}})

となります. この手法による概念消去はカスタマイズ性が高く, 簡単に共有できますし, ストレージもadapter分しか占有しません (他の手法だとOriginal U-Netに加えてfine-tuned U-Netができます).

Latent Anchoring

fine-tuningを通して, specialized conceptsの半透明性を獲得します. これではなんのことかさっぱりわかりませんが, 既存手法と似たようなことが行われます. 細かくみていきます.

消したい概念 c_{tar} が与えられたとき, 概念消去後のモデルの振る舞いを表す代理概念 c_{sur} を事前に用意します. その後, c_{tar} と c_{sur} の確率分布を一致させるように学習します.

\mathcal{L}_{era}=\mathbb{E}_{x_t, t}[\|\varepsilon(x_t, c_{tar}, t\mid\theta, \mathcal{M}_{c_{tar}})-\varepsilon(x_t, c_{sur}, t\mid\theta)+\eta*(\varepsilon(x_t, c_{tar}, t\mid\theta)-\varepsilon(x_t, c_{sur}, t\mid\theta))\|_2^2]

\eta は消去の強度を表します.

さて, 概念消去では他の概念への影響が心配されます. 既存研究であるConcept Ablation (ConAbl)やSelective Amnesia (SA)では生成して再学習というアプローチをとっています. 具体的には収集したテキストから画像を生成し, そのペアを用いて再学習をしています. しかし, この方法は2つの問題を抱えています.

  1. テキストは数千のスケールでしかなく, 手作りなので潜在的なバイアスを抱えている.

    • ここでは拡散モデルが取得した意味空間と人間が持つ意味空間が異なることを表します.

  2. テキストを準備するのは大変だし, そこから画像を生成するのはもっと大変.

    • SAではテキストを事前に用意しても80GPU時間以上が生成に費やされており, 手軽とは全く言えません.

これに対処するのがLatent Anchoringになります. 先に目的関数を確認します.

\argmin_{\theta}\mathbb{E}_{c\in\mathcal{C}}[\|\varepsilon(x_t, c, t\mid\theta, \mathcal{M}_{c_{tar}})-\varepsilon(x_t, c, t\mid\theta)\|_2^2]

です. これはSPM付きのモデルの予測結果とOriginalの予測結果が同じになるように学習することを表します. \mathcal{C} はtext encoderの持つ意味空間です.

しかし, この形式は \mathcal{C} が原因で学習が難しいです. それに加えて消去を行う損失と逆行しています. そのため, \mathcal{C} からサンプリング分布 \mathcal{D}(\cdot|c_{tar}) を取り出して簡単な形にします. 目標は, 対象概念から離れた概念は元のモデルと一貫性をしめすことです. ここでの距離概念はcosine-similairtyで定義されます. この状況でサンプリング確率を次のように定めます.

P_{c\sim\mathcal{D}(\cdot|c_{tar})}(c|c_{tar})\propto\left(1-\dfrac{|c\cdot c_{tar}|}{\|c\|\cdot\|c_{tar}\|}\right)^\alpha

\alpha はハイパーパラメータです. すると, 損失関数は

\mathcal{L}_{anc}=\mathbb{E}_{{c\sim\mathcal{D}(\cdot|c_{tar})}}[\|\varepsilon(x_t, c, t\mid\theta, \mathcal{M}_{c_{tar}})-\varepsilon(x_t, c, t\mid\theta)\|_2^2]

です. 最後にハイパーパラメータ \lambda を乗じて

\mathcal{L}=\mathcal{L}_{era}+\lambda\mathcal{L}_{anc}

です.

Facilitated Transport

ここまでの過程を経ると, SPMはモデルに依存しない消去コーパスを構築します. これは普遍的で包括的なので他の拡散モデル \tilde{\boldsymbol{W}} に適用可能です. k 個の概念を消すとすると,

\boldsymbol{y}=\tilde{\boldsymbol{W}}\boldsymbol{x}+\sum_{c}^k(\gamma^c\cdot\boldsymbol{v}_{reg}^{cT}\boldsymbol{x})\cdot\boldsymbol{v}_{sig}^c

論文の記法をそのまま用いているので紛らわしいのですが, T は転置ですので \boldsymbol{v}_{reg}^{c} を転置するということです.

先ほどのLatent Anchoringでは他の概念を維持するように設計されていますが, 複数のSPMが組み合わさる状況ではどうしても互いに影響し合ってしまいます. 例えばあるSPMでは概念Aを消去していますが, 別のSPMでは概念Bを消去している場合, このSPMではAは維持されています. これら2つのSPMを組み合わせると概念Aと概念Bが同時に消えて欲しいですが, ただ組み合わせるだけではそうはいきません. こうした現象を最小限に抑えるのが推論段階で導入されるFacilitated Transportです.

具体的には, プロンプト p が与えられたとき, 各SPMにおける情報透過性と伝送率を表す \gamma^c(p) は, p に示された対象概念 c の確率に依存します. この確率を推定するためにCLIPを用いてcosine distance s_f^c(p) を計算します. token-levelでの類似性を特定するにはuni-gramな指標の追加が必要です.

s_t^c(p)=\dfrac{|T(c)\cap T(p)|}{|T(c)|}

T はtokenizerです. これによって, 概念cが p に現れる確率を以下のように導出します

\gamma^c(p)=\max(s_f^c, s_t^c)

プロンプトがSPMを意味的に刺激するときは \gamma が増幅して, 動的に消去信号が発せられます. 逆にそうでないときはtransportが無効になります.

実験

Concept Removal

まずは概念消去の能力を確認します. Snoopyを消去し, Mickey, Spongebob, Pikachu, Dog, Legislatorの影響を確認します. “graffiti of the {concept}”で生成を行った結果を示します.

ConAblやSAではdogを生成した際にgraffitiというスタイルが失われていることが確認できます. また, ESDはMickeyでの生成でMickeyが確認できません. 一方で提案手法は非常にOriginalと見た目が同じものが生成されています.

続いて, 複数概念の消去結果を見ます.

例えばMickeyの生成例ではESDとConAblはSnoopyを消した段階でMickeyの生成にも失敗しています. SAもLegislatorの例では変な生成例になっていることがわかります. このように, target concept以外の概念は既存手法はあまり性能が良くないように見えます.

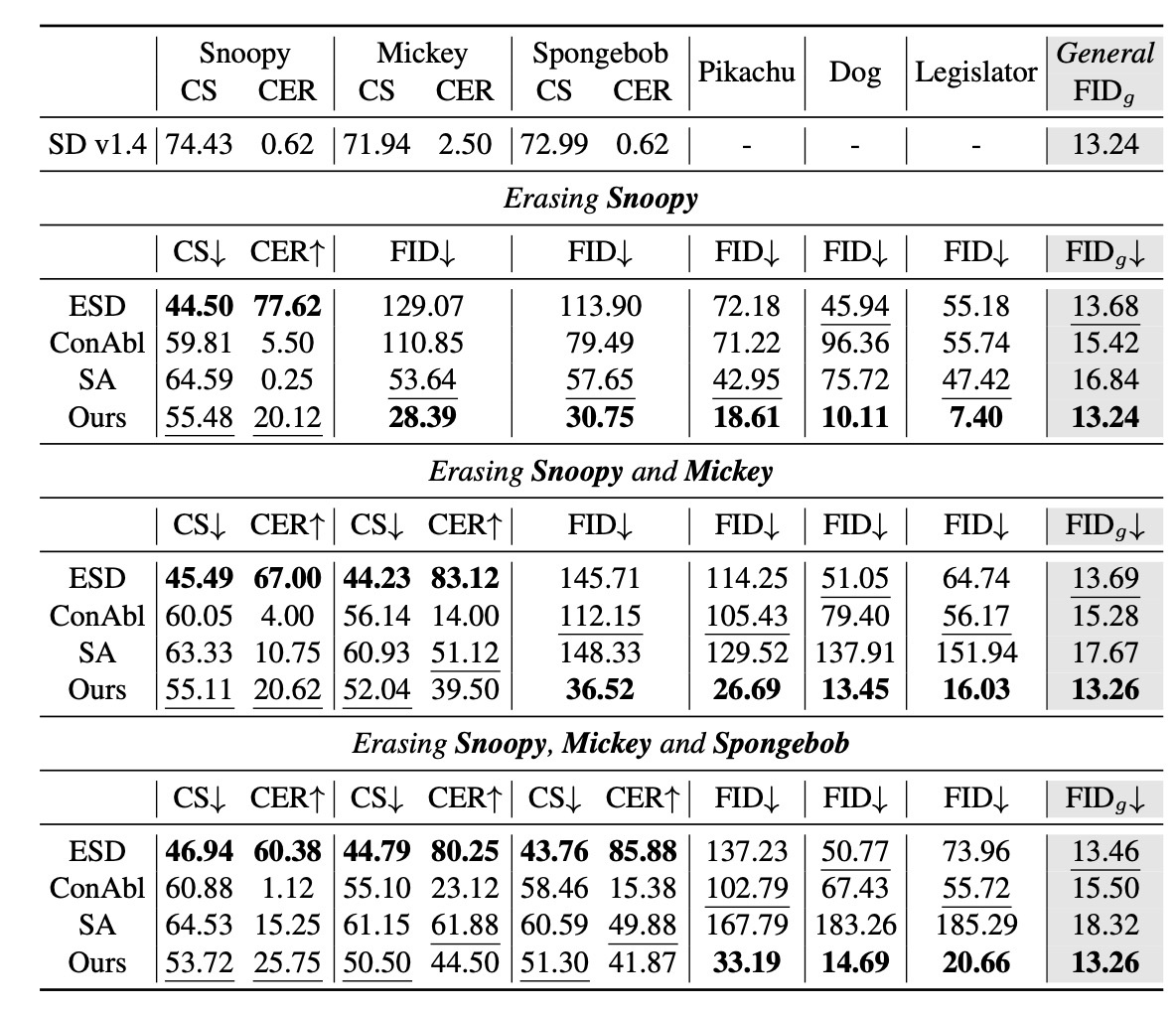
続いて, 定量評価を見てみます. ここでは, CLIP Score (CS), CLIP Error Rate (CER), FID, FID_gを用います. FIDはOriginal SDの生成画像を, FID_gはCOCO-30kの画像を比較対象とします.

例えばSnoopyの場合を見てみると, ESDがCS, CERともに最もよく, 削除性能は高いです. しかし, 他の概念に対するFIDを見てみると, MS-COCOのFIDはそうでもないですが, 意味的に似ているMickeyなどの概念では非常に大きい値が出ており, 他の概念への侵食性が明らかになります. ConAblやSAでは生成して再学習というプロセスなので一般的な生成性能であるFID_gは悪いです. この傾向は複数の概念を消去した場合にも現れていることが確認できます.

続いて, 計算効率を確認します.

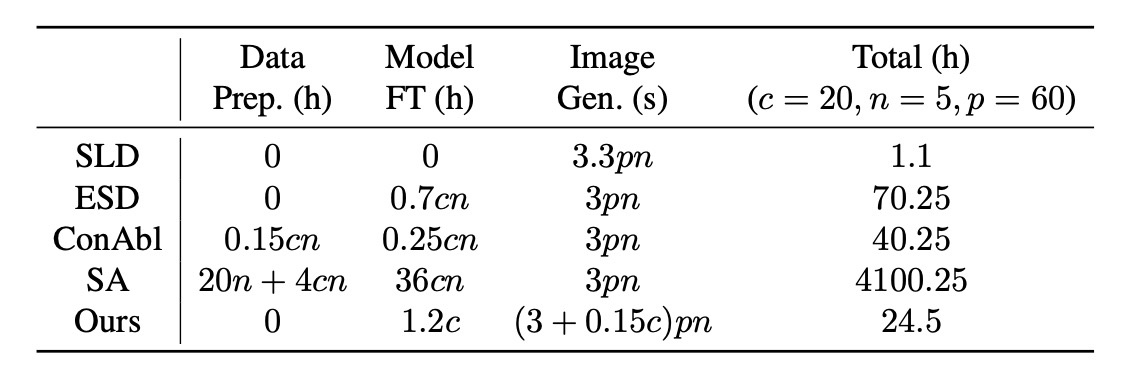
n 個の拡散モデルに対して c 個の概念を消去する際に要する時間の比較です. p はそのパイプラインで用いられるプロンプトの数です. この実験では基本的にNVIDIA A100 GPUが1個使われますが, 複数のGPUを用いる場合はそれだけ時間消費量が増加すると述べられています. 論文で想定するケースは c=20, n=5, p=60 ですが, SLDを除く既存手法より大幅に高速に行われることがわかります. ここで, ベースラインでもないSLDが登場した理由は不明です.

Training-Free Transfer Study

Stable Diffusion 1.4を用いて作成したSPMのモデルを他のコミュニティモデルに移植することを考えます. ここでは, Stable Diffusion 1.5やChilloutmix, RealisticVision, Dreamshaper-8を用います.

確かに消したい概念については消せており, 他の概念への影響は軽微です.

多彩な消去

これまではオブジェクトに限って性能を確認していました. 以降では一般の概念に対象を拡大して調べます.

まずはスタイルの消去です. Gogh styleとPicasso styleを消去した場合の結果が示されています.

ESDとConAblではGoghのスタイル消去に成功していますが, Picassoは消せていません. それはSAも同様です. 提案手法はオブジェクト同様の結果が出ていると著者らは主張しています.

しかし, 個人的にはGogh styleの消去結果は微妙なのではと思います. それは絵ではなくなっているからです. 意味空間でGogh styleとrealistic photoが近いのではと思いますが, 反映しているプロンプトは"A vase of vubrant flowers"までになっているように思えます.

続いて, I2P benchmarkでの生成例のうち, NudeNetでどの程度検知できたかを確認します. 既存研究同様の評価手法です.

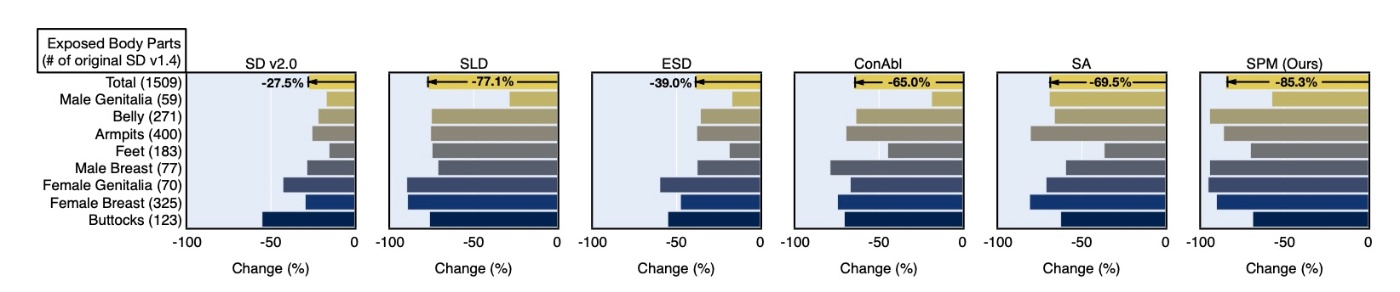
Stable Diffusion 1.4と比較してどの程度減ったかを表しますが, 提案手法は非常に高い消去性能であることがわかります. 先ほど確認したように, 他のモデルへの移植が可能なので概念消去により強い汎用性をもたらすことができます.

最後に, memorized imageを確認します. こちらも成功していることがわかります.

まとめ

  • PEFTベースの手法であるSPMの提案
  • 増加するモデルサイズも非常に小さい (増加率は0.0005)
  • 他の概念への影響がかなり少なく, それに加えて既存手法よりも強い消去性能
  • 他のモデルへの転送が可能なので概念消去を使い回す必要がない

思ったこと

  • 他のコミュニティモデルへの転送可能性は今までになかった着眼点で新規性があると思います.
  • 消していない概念への影響が非常に軽微で, コピペしたんじゃないかと思うくらいのものになっていて驚きました.
    -　恐らく論文通りに実装すると1つの概念につき1つのアダプターができると思いますが, いくつも概念を消そうとすると管理が大変そうな気がします.
  • 明言はされていませんが, 公式実装を確認するとPEFTのうち, LoRAを用いています. 他のPEFT手法 (例えばQLoRAやVeRAなど)を用いたらどうなるのかは気になります (PEFT手法依存とは思えませんが).
  • Stable Diffusion 2.0などには転送できないのでしょうか. attention head dimが異なるのでできなさそうな気はします.

参考文献

  • Lyu, M., Yang, Y., Hong, H., Chen, H., Jin, X., He, Y., Xue, H., Han, J., and Ding, G. One-dimensional adapter to rule them all: Concepts diffusion models and erasing ap- plications. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7559–7568, June 2024.

Changelog

  • CVF公開によるリンクの追加, および書籍情報の更新 (2024/08/26)

Discussion