🚲

UE5 Niagara で 3D Gaussian Splatting を描画する

2023/12/02に公開

Unreal Engine

機械学習

UE5

tech

「Unreal Engine (UE) Advent Calendar 2023 その2」2日目の記事です。

3D Gaussian Splattingは簡単にリアルなシーンが作れて楽しいですね。
その描画に必要な処理をNiagaraで実装し、UE5で描画する方法を解説します。
1から10までのステップバイステップのガイドというより、描画の原理を理解することを目的としたドキュメントです。
なお、本稿で述べる方法はUE Marketplaceのこちらの商品に実装されています。

背景

3D Gaussian Splattingのデータ表現形式

3Dモデルを「楕円体」（ラグビーボールのような立体）の集合として表現します。点群に似ていますが、個々の点が「点」ではなく「楕円体」になっているイメージです。

個々の「楕円体」は位置・向き・サイズ（UE風に言えばTransform）とRGBAの色を持ちます。描画時は、3次元ガウス分布にしたがって各楕円体の端に行くほど色が薄くなるように描画します。

この表現形式のいいところは（私の理解では）下記の２点です。

大きさのない「点」ではなく大きさのある「楕円体」の集合であるため、立体物を表現することができる
「楕円体」の中の3次元ガウス分布を効率的に2次元のスクリーンに投影して描画する手法が確立されており、高速^[1]に描画できる

3D Gaussian Splattingの描画方法

上記のようなデータは、スプライト^[2]を使ったパーティクルとして描画することができます。
具体的には

カメラから見た画面上での「楕円体」の位置を計算する
カメラから見た画面上での「楕円体」の向きと大きさを計算する
計算した位置・向き・大きさで画面上に矩形のスプライトを置く
スプライトの中を端に行くほど薄くなるように色を塗る

という処理を行えばよいです。

1と3は、エンジン標準のパーティクルシステムであるNiagaraで簡単に実現できます。

2は、3D Gaussian Splattingの論文の「4. DIFFERENTIABLE 3D GAUSSIAN SPLATTING」の式(4)～(6)

G(\vec{x}) = e^{- \frac{1}{2} \vec{x}^T \Sigma^{-1} \vec{x}}　　　(4)

\Sigma' = JW \Sigma W^T J^T　　　(5)

\Sigma = RS S^T R^T　　　(6)

にしたがって、3次元ガウス分布(4)を下記のように画面座標系 $\vec{x_s}$ で表してやるという計算に帰結します。

G(\vec{x_s}) = e^{- \frac{1}{2} \vec{x_s}^T \Sigma'^{-1} \vec{x_s}}

= e^{- \frac{1}{2} \vec{x_s}^T (JWRS S^T R^T W^T J^T)^{-1} \vec{x_s}}　　　(※)

（ $S$ は、3次元ガウス分布のローカル座標系での各軸方向のサイズを決める対角行列）
（ $R$ は、3次元ガウス分布のLocalToWorld変換）
（ $W$ は、カメラのWorldToView変換）
（ $J$ は、ViewToClipおよび画面座標への変換に相当するヤコビ行列）
（ただし $J$ は、透視投影の非線形な変換をテイラー展開して近似しています。詳細はEWA Splattingの式(26)～(29)を参照）

式(※)をしばらく眺めていれば直観的に「ローカル座標系で表された3次元ガウス分布を画面座標系に変換する」みたいなことをしているんだなと理解できるはずです。

「直観的にわからないが？！」
という未来の自分のために、もう少し解説を書いてみたので、詳しく知りたい場合は下記をどうぞ。

1次元ガウス分布の数学的表現

ガウス分布（正規分布とも言う）は、確率を扱う分野ではよく出てくる分布です。
一次元空間でのガウス分布は下記の式で表されます。

G(x) = exp(- \frac{1}{2} \frac{x^2}{\sigma^2})

我々が知っておくべきポイントは下記の2点です。

原点（ $x=0$ ）をピークとして、そこから離れるほど値が小さくなる
値の小さくなり方は、標準偏差（ $\sigma$ ）で決まる

3次元ガウス分布の数学的表現

上記を3次元空間に拡張したものが下記の式で表される3次元ガウス分布です。

G(\vec{x}) = exp(- \frac{1}{2} \vec{x}^T \Sigma^{-1} \vec{x})　　　(4)

ただし、 $\vec{x}$ は3次元のベクトル、 $\Sigma$ は3x3の対称行列です。
ポイントは下記の2点です。

原点をピークとして、そこから離れるほど値が小さくなる（一次元の場合と同じ）
値の小さくなり方は、行列 $\Sigma$ で決まる

3次元ガウス分布が対角成分のみを持つ場合

$\Sigma$ の意味を考えるために、 $\Sigma$ がシンプルな対角行列である場合について考えます。

\Sigma = \begin{pmatrix} \Sigma_x & 0 & 0 \\ 0 & \Sigma_y & 0 \\ 0 & 0 & \Sigma_z \end{pmatrix}

式(4)に代入して変形すると、XYZ軸に沿った方向に一次元のガウス分布を考え、それらの積を取っただけであることがわかります。

G(\vec{x}) = exp(- \frac{1}{2} \vec{x}^T \begin{pmatrix} \Sigma_x & 0 & 0 \\ 0 & \Sigma_y & 0 \\ 0 & 0 & \Sigma_z \end{pmatrix}^{-1} \vec{x})

= exp(- \frac{1}{2} \begin{pmatrix} x & y & z \end{pmatrix} \begin{pmatrix} \frac{1}{\Sigma_x} & 0 & 0 \\ 0 & \frac{1}{\Sigma_y} & 0 \\ 0 & 0 & \frac{1}{\Sigma_z} \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix})

= exp(- \frac{1}{2} (\frac{x^2}{\Sigma_x} + \frac{y^2}{\Sigma_y} + \frac{z^2}{\Sigma_z}))

= exp(- \frac{1}{2}\frac{x^2}{\Sigma_x})・exp(- \frac{1}{2}\frac{y^2}{\Sigma_y})・exp(- \frac{1}{2}\frac{z^2}{\Sigma_z})

つまり、対角成分のみの場合は、対角成分が各軸方向のガウス分布の標準偏差の2乗になっているということです。

これを3次元空間上にプロットすると、空間の軸とガウス分布の軸がぴったり一致する場合であることがわかります。

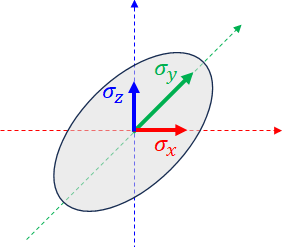
ここまでの議論を整理すると、

S = \begin{pmatrix} \sigma_x & 0 & 0 \\ 0 & \sigma_y & 0 \\ 0 & 0 & \sigma_z \end{pmatrix}

という行列を考え、

\Sigma = SS = SS^T = \begin{pmatrix} \sigma_x^2 & 0 & 0 \\ 0 & \sigma_y^2 & 0 \\ 0 & 0 & \sigma_z^2 \end{pmatrix}

としてやると、 $\Sigma$ が対角成分のみを持つ場合（空間の軸とガウス分布の軸が一致する場合）は、各軸方向の標準偏差 $\sigma_x$ , $\sigma_y$ , $\sigma_z$ で定義される行列 $S$ を使って、

G(\vec{x}) = exp(- \frac{1}{2} \vec{x}^T (SS^T)^{-1} \vec{x})

という形で3次元ガウス分布を書くことができるというわけです。

3次元ガウス分布が任意の方向を向いている場合

では、空間の軸とガウス分布の軸が一致しない場合はどうなるかというと、ガウス分布の向きを決める回転行列Rを考えて、

\Sigma = R S S^T R^T

G(\vec{x_w}) = exp(- \frac{1}{2} \vec{x_w}^T (R S S^T R^T)^{-1} \vec{x_w})

としてやればよいです。

この式はぱっと見は難解ですが、世界座標 $\vec{x_w}$ をガウス分布のローカル座標系 $\vec{x_L}$ に $R$ で変換してから対角成分のみを持つ3次元ガウス分布を評価していると解釈することができます。
つまり、

\vec{x_w} = R\vec{x_L}

とおけば、上式は、

G(\vec{x_L}) = exp(- \frac{1}{2} (R\vec{x_L})^T (R S S^T R^T)^{-1} R\vec{x_L})

= exp(- \frac{1}{2} \vec{x_L}^T R^{-1} (R S S^T R^T)^{-1} R\vec{x_L})

= exp(- \frac{1}{2} \vec{x_L}^T (R^{-1} R S S^T R^T R)^{-1} \vec{x_L})

= exp(- \frac{1}{2} \vec{x_L}^T (SS^T)^{-1} \vec{x_L})

となるというわけです。

UE風に言うと、アクターのローカル座標で考えれば簡単になるよ、みたいな感じですね。

3次元ガウス分布の画面への投影

ここまでで式(4)と(6)は解説できました。
ここからは式(5)で表される「カメラから見たときどう見えるか」について考えます。

まず、世界座標系からカメラのView座標系への変換を考えます。
といっても、原点は別途適当にシフトしてもらうとすれば、単にカメラの向きだけガウス分布を回転させればいいので、先の $R$ を掛けたのと全く同じ議論で、下記のようにしてやればよいだけです。

G(\vec{x_c}) = exp(- \frac{1}{2} \vec{x_c}^T (WRS S^T R^T W^T)^{-1} \vec{x_c})

ただし、 $W$ はカメラのView行列、 $\vec{x_c}$ はカメラのView座標系です。簡単ですね。

あとはこれを透視投影して画面座標系に直してやればゴールなのですが、透視投影は非線形なので単純な行列の掛け算では本当は表せません。
なのですが、まあガウス分布の中心近傍でテイラー展開して近似してやればいいよねということで、ヤコビ行列 $J$ をうまく定義して掛け算します。

G(\vec{x_s}) = exp(- \frac{1}{2} \vec{x_s}^T (JWRS S^T R^T W^T J^T)^{-1} \vec{x_s})

ただし、 $\vec{x_s}$ は画面座標系（ピクセル位置）です。
Jの考え方はEWA Splattingの式(26)～(29)あたりを眺めるとわかる。

上式のz(奥行方向)を捨ててスクリーン上のxy二次元で考えて、全ての(x, y)について上式を評価してやれば画面上でのガウス分布の密度がわかるので、あとはこれをガリガリ描画してやればよいだけです。

長かった～

4は、上記2で求めた画面座標系でのガウス分布 $\Sigma'$ にしたがってピクセルシェーダを走らせるだけです。

UE5で実装する

先の描画方法の通りUE5で実装していきましょう。全体の流れは下記の通りです。

データをインポートしてガウス分布の位置、向き、サイズ、色をテクスチャに書き出しておく
Niagaraで位置テクスチャを参照してパーティクルを生成する
Niagaraでカメラ情報、パーティクル位置、向きテクスチャ、サイズテクスチャを参照して、画面座標系でのガウス分布を求める
Niagaraスプライトレンダラーでスプライトを生成する
Materialで画面座標系でのガウス分布にしたがって透明度を計算しスプライトを描画する

0. データのインポート

2023年現在の3D Gaussian Splattingの多くの実装では.ply形式でデータを出力します。
.plyファイルのヘッダはプレーンなテキストで記載されており、テキストエディタでファイルを表示すると読むことができます。

ということで、適当なデータをテキストエディタに放り込むとこんな感じになります。

ply
format binary_little_endian 1.0
element vertex 1068277
property float x
property float y
property float z
property float nx
property float ny
property float nz
property float f_dc_0
property float f_dc_1
property float f_dc_2
property float f_rest_0
property float f_rest_1
property float f_rest_2
property float f_rest_3
（中略）
property float f_rest_44
property float opacity
property float scale_0
property float scale_1
property float scale_2
property float rot_0
property float rot_1
property float rot_2
property float rot_3
end_header
������;�?��
…
（この後バイナリデータが延々とつづく）

3行目に頂点（ガウス分布）の数が記載されており、4行目～end_headerまででその後のBody部分のデータ構造を定義しています。
とりあえずこの構造でバイナリデータを読み込んでプロットしたりして眺めていると、どうやら下記のことがわかってきます。

x,y,zはガウス分布の中心位置
nx,ny,nzは全部0で使われていない（ノーマル？）
f_dc_0 ～ f_dc_2は、ガウス分布のRGB色
opacityは、ガウス分布の透明度
scale_0 ～ scale_2は、ガウス分布のサイズ
rot_0 ～ rot_4は、ガウス分布の向き
f_rest_0 ～ f_rest_44は、消去法で考えるとSpherical Harmonicsの高次項の係数っぽい

ということで、これらを適当にOpenEXRなどを使ってFloatの画像ファイルにしてUEにインポートすればいいわけですが、いくつか注意があります。

データ作成元によっては座標系の向きがUEとちがう。多くの場合、UEのZ-up左手系に合わせるための変換が必要。
データ作成元によっては各種値にActivation関数を適用する必要がある。公式実装の場合は下記の通り。
- opacityにはSigmoid関数を適用する
- scaleには指数関数を適用する

opaciyとscaleについてだけ書けば、

float opacityActivated = 1.0f / (1.0f + FMath::Exp(-opacity));
float scaleActivated_x = FMath::Exp(scale_x);
float scaleActivated_y = FMath::Exp(scale_y);
float scaleActivated_z = FMath::Exp(scale_z);

という感じですね。

1. Niagaraで位置テクスチャからパーティクルを生成する

Niagaraでテクスチャを読み込んでそのデータに基づいてあれこれするにあたり、参考になるのはContentExamplesプロジェクトの「/ExampleContent/Niagara/Textures/TextureSampling_System」です。

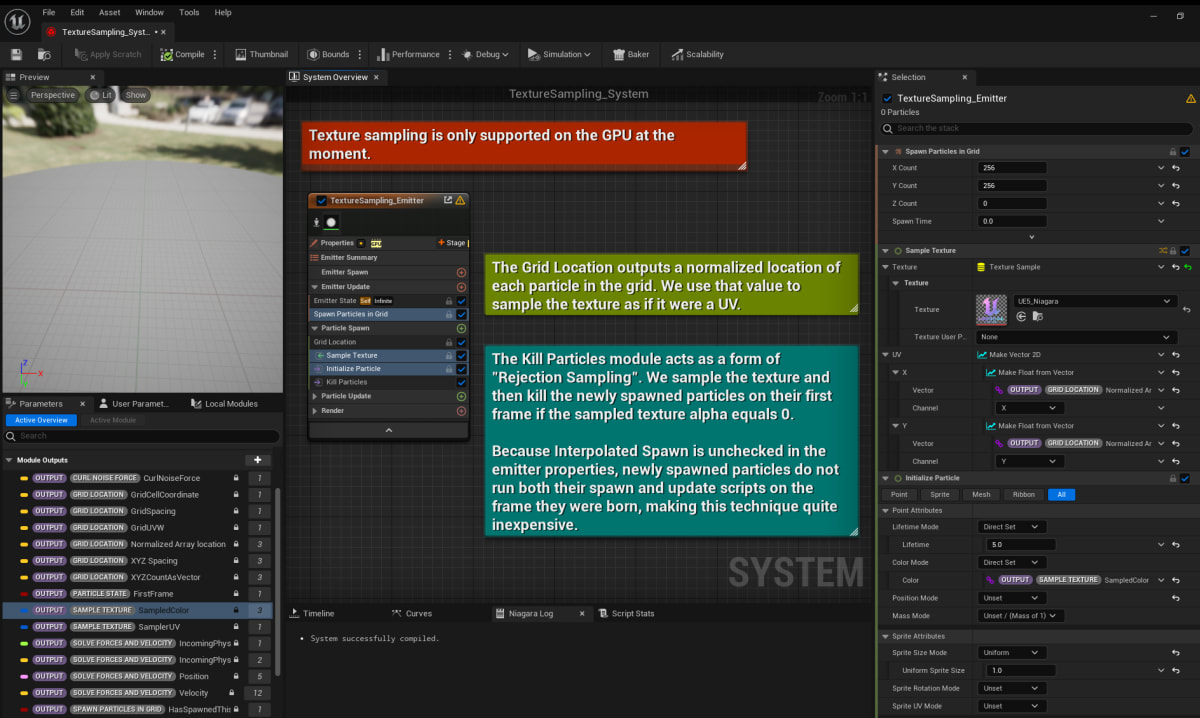
こいつが何をやっているかというと

Spawn Particle in Grid でテクスチャの解像度に合わせたパーティクルを生成する（上記画像の場合は256x256）
Sample Texture モジュールで、グリッド上に生成したパーティクルの位置をUV座標に変換して、各パーティクルごとに1ピクセルのデータを読み込む
Module Outputs に「(OUTPUT) (SAMPLE TEXTURE) SapledColor」が自動で追加されるので、このfloat4値であれこれする（上記画像の場合はInitialize Particleで色を設定）

ということをしています。
我々の場合は、位置テクスチャから読み込んだ値でInitialize Particleモジュールで位置をセットしてやればよいです。

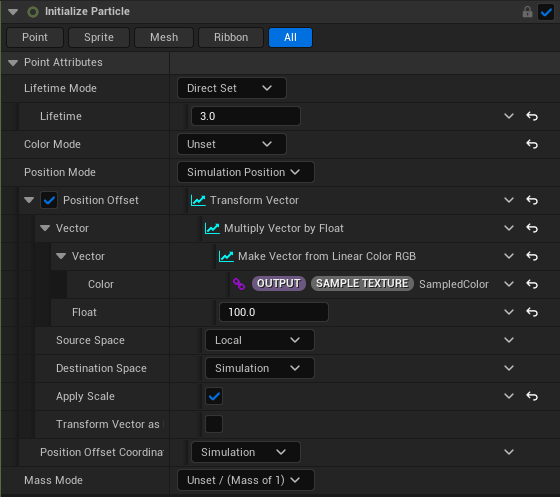
UEのセンチメートルスケールにあわせて100倍したり、ローカル座標からシミュレーション座標に変換などもしておくとよいでしょう。

2. Niagaraで画面座標系でのガウス分布を求める

一番大事な部分です。
Sample Texture モジュールで向き、サイズを読み取り、カメラ情報と合わせて式(※)の $J^TW^TR^TS^TSRWJ$ を計算します。

Particle Update に新規 Scratch Pad モジュールを追加してそこに計算を書いていきます。

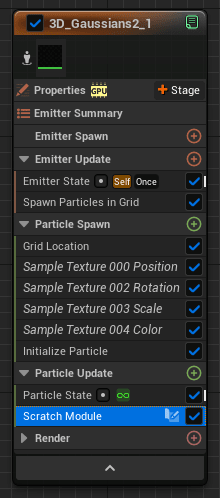
（向き、サイズ、ついでに色のテクスチャを読み込むモジュールも追加しておきました）

スケール行列 $S$

一番簡単で、対角行列を作るだけです。
というか、その処理を書く必要すらなく、Niagaraにそのためのノードが用意されています。
テクスチャから読み取った値をVectorにして渡すだけです。

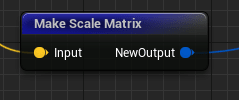
回転行列 $R$

これも簡単で、QuatをMatrixに変換するだけです。
やはりNiagaraにそのためのノードが用意されています。
テクスチャから読み取った値をQuatにして渡すだけです。

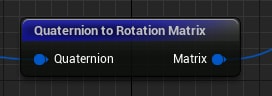
View行列 $W$

Camera Data InterfaceからのMap Getでプレイヤーのカメラの情報にアクセスできます。

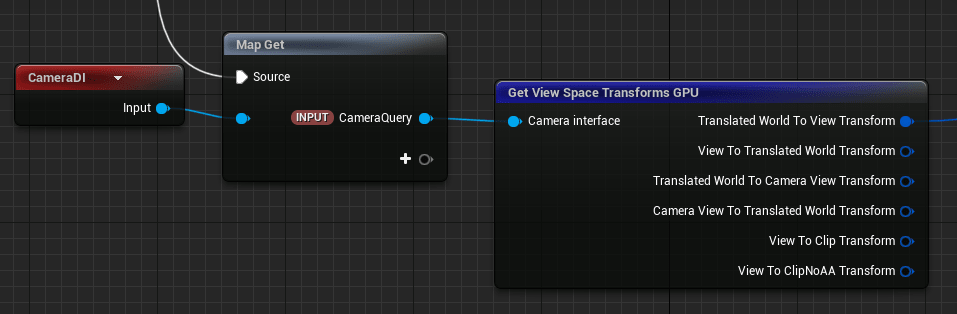
WorldToViewなのかViewToWorldなのか迷いどころですが、全ての転置の組み合わせを試せば正解がわかるのでがんばりましょう。
私はいまだによくわかっていないです。

ヤコビ行列 $J$

View空間でのガウス分布の中心座標 $\vec{x_v}$ とカメラの焦点距離 $f$ から、下記のように計算します。

J = \begin{pmatrix} f / z_v & 0 & -f * x_v / z_v^2 \\ 0 & -f / z_v & - f * y_v / z_v^2 \\ 0 & 0 & 0 \end{pmatrix}

ということで、 $\vec{x_v}$ と $f$ を求めましょう。

View空間でのガウス分布の中心座標 $\vec{x_v}$

世界座標でのガウス分布の中心はパーティクル位置として既に計算済みなので、そこにカメラのWorldToView行列をかけてやればよいです。
TranslatedWorldを使う場合はPreViewTranslationを足してやる（カメラの位置に原点をシフトする）ことを忘れないようにしましょう。

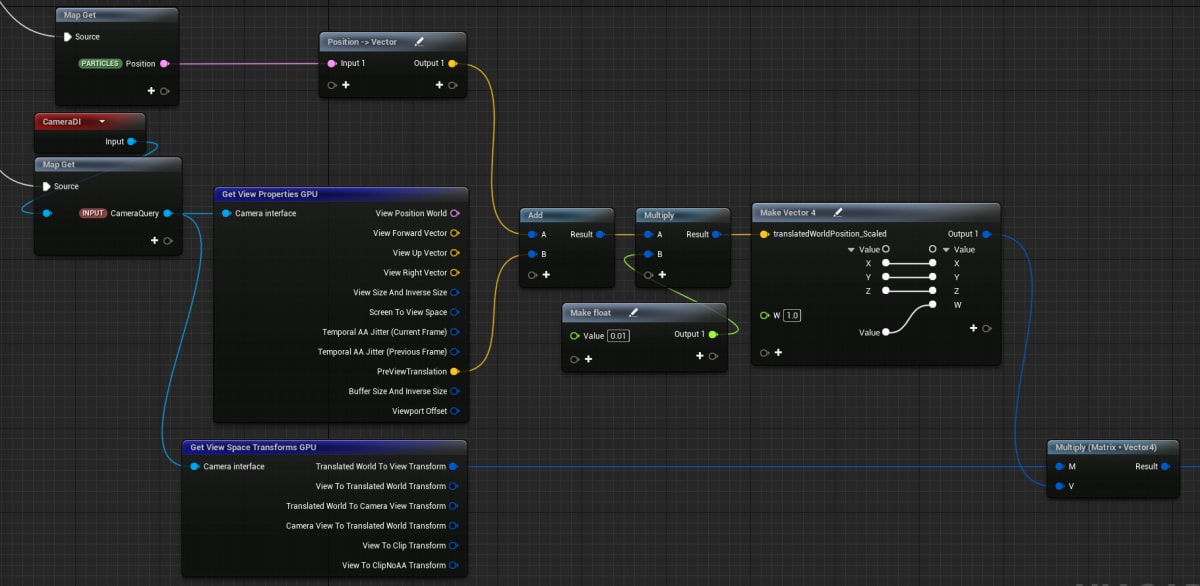
焦点距離 $f$

FOVと画面サイズで計算できます。
ViewToClip行列から値を取り出す等のもっとスマートな方法がありそうな気がしますが、とりあえずこれで動くのでこうしています。

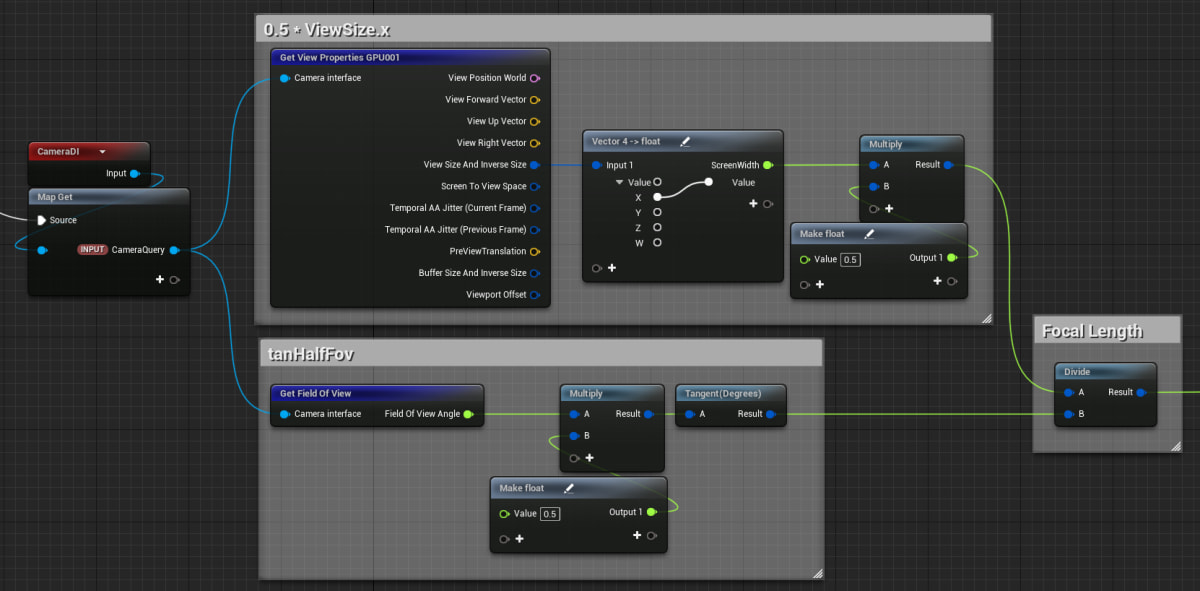
あとは掛け算するだけ…

$S$ 、 $R$ 、 $W$ 、 $J$ が揃ったので、あとはこれらの転置を取ったりしながら掛け算して逆行列を取るだけです。

もしあなたが完全に理解していればなにも問題ないと思いますが、私のように雰囲気でしか理解していない場合、ここで各行列の転置がどっちがどっちだかわからなくなります。
（例えば、Rの元になっているQuatって、どういう定義でデータに記録されているんだ？あとアクターの回転も入れ込むにはこれどっちに回せばいいんだ？等々）
でも、所詮 $2^{4}$ 程度の組み合わせしかないので、総当たりすれば楽勝です。

計算結果 $\Sigma'^{-1}$ は DynamicMaterialParameter にでも突っ込んでおきましょう。
これは、各パーティクルごとに任意のデータをマテリアルに渡すために最初から標準で備わっている変数です。

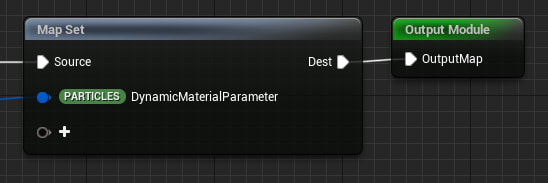
3. Niagaraスプライトレンダラーでスプライトを生成する

実際に画面上に表示するために、Sprite Rendererモジュールを追加します。

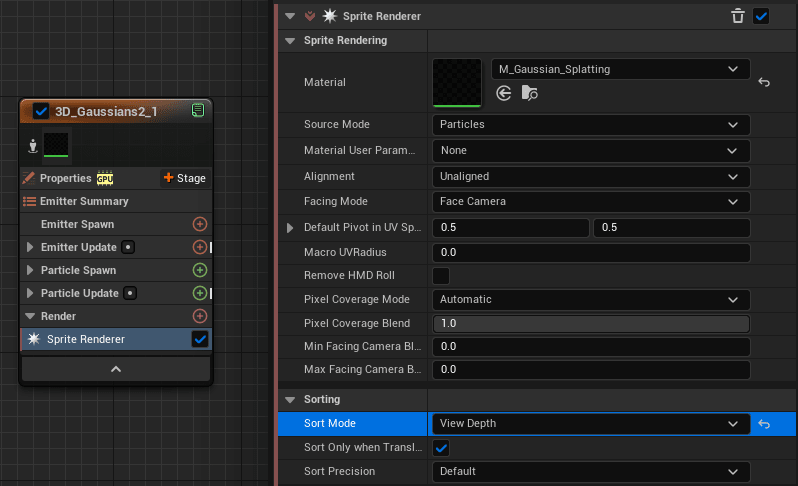
マテリアルは新規に作成し、それをセットしておきます（マテリアルの中身は後述）。
また、Sorting > Sort Mode を View Depth にしておきます。半透明マテリアルを多数重ねて描画するので、奥行方向にソートした上で順番に描画する必要があるからです。

4. Materialで透明度等を計算しスプライトを描画する

透明度

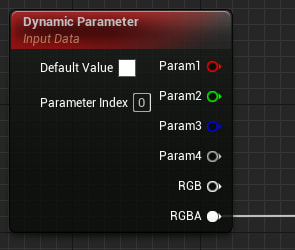
画面座標系でのガウス分布の情報 $\Sigma'^{-1}$ を DynamicMaterialParameter から取得します。

これを使って、各ピクセルでのガウス分布の密度＝スプライトの透明度を計算します。

G(\vec{x_s}) = exp(- \frac{1}{2} \vec{x_s}^T \Sigma'^{-1} \vec{x_s})

上式を計算するためには、各ピクセルのガウス分布の中心からの相対位置 $\vec{x_s}$ が必要です。

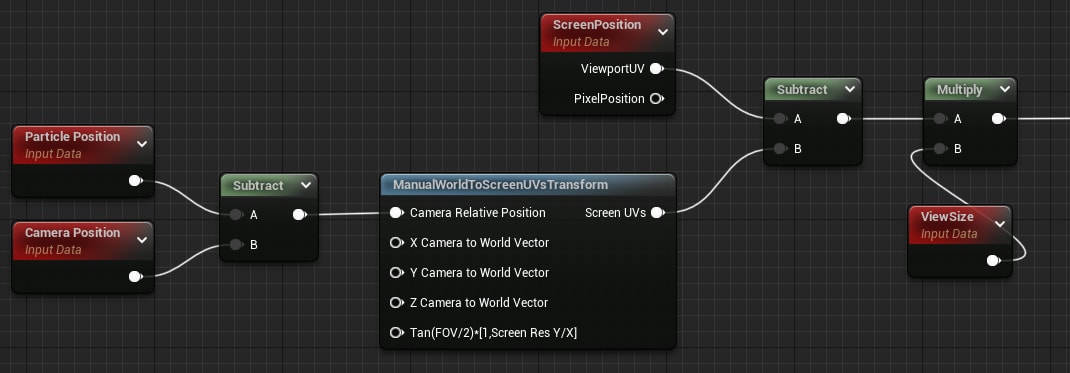
Particle Positionノードでガウス分布中心の世界座標系での位置がわかるので、これを元にまずは画面座標系での中心を求めます。
といっても、Camera Positoinとの相対位置にしてからManualWorldToScreenUVsTransformに渡してやるだけです。
これで中心のビューポート上でのUV座標がわかるので、現在のピクセル位置のUV座標との差をとって、スクリーン解像度を掛けてやれば、ほしかった相対位置 $\vec{x_s}$ が手に入ります。

あとは上式の計算結果に個々のガウス分布それ自体のopacityを乗算すれば最終的な透明度となります。

色

ここまで説明を省略してきましたが、3D Gaussian Splattingのデータに記録されている色はSpherical Harmonicsの係数です。
つまり、ガウス分布を見る方向（＝ガウス分布の位置 - カメラ位置）に基づいて下記のような計算をしてやる必要があります。

float3 direction = WorldPosition - CameraPosition;
float x = direction.x, y = direction.y, z = direction.z; //必要に応じてここに座標系の変換を入れ込む
float xy = x * y, xz = x * z, yz = y * z, x2 = x * x, y2 = y * y, z2 = z * z, xyz = xy * z;

float3 Color = 0.5f
    + 0.28209479177387814f                                    * ShCoeff0 //float3(f_dc_0, f_dc_1, f_dc_2)
    - 0.48860251190291987f * y                                * ShCoeff1
    + 0.48860251190291987f * z                                * ShCoeff2
    - 0.48860251190291987f * x                                * ShCoeff3
    + 1.0925484305920792f * xy                                * ShCoeff4
    - 1.0925484305920792f * yz                                * ShCoeff5
    + (0.94617469575755997f * z2 - 0.31539156525251999f)      * ShCoeff6
    - 1.0925484305920792f * xz                                * ShCoeff7
    + (0.54627421529603959f * x2 - 0.54627421529603959f * y2) * ShCoeff8
    + 0.59004358992664352f * y * (-3.0f * x2 + y2)            * ShCoeff9
    + 2.8906114426405538f * xy * z                            * ShCoeff10
    + 0.45704579946446572f * y * (1.0f - 5.0f * z2)           * ShCoeff11
    + 0.3731763325901154f * z * (5.0f * z2 - 3.0f)            * ShCoeff12
    + 0.45704579946446572f * x * (1.0f - 5.0f * z2)           * ShCoeff13
    + 1.4453057213202769f * z * (x2 - y2)                     * ShCoeff14
    + 0.59004358992664352f * x * (-x2 + 3.0f * y2)            * ShCoeff15
    ;
return Color;

これをNiagaraでやるかMaterialでやるかは考慮の余地があります。

Niagaraでやる：ガウス分布ごとに計算することができる
Materialでやる：頂点ごとやピクセルごとに計算することができる

ガウス分布の中心一か所で代表させて計算量を省略したければNiagaraで計算してParticle Colorに設定すればMaterialに色を渡せるし、頂点ごとやピクセルごとにより細かく色を表現したければ上記をMaterialで計算すればよいです。

まあ、そんなこと考えずに0次の項だけ計算して高次項は無視ってしても違いに気づく人はほとんどいませんが。

あと、上記の結果出てくる色は学習元データの写真の色空間なので、大抵の場合は最後にリニアカラーに変換してやる必要があることに注意してください。

最後に

3D Gaussian Splattingの描画プラグインを作るためにほぼ初めてNiagaraを触りました。
Niagaraはまだまだネット上に情報が少ないので、私の実装が何かの参考になれば幸いです。

ちなみに現在、本稿で説明したのとは全く異なるアイデアでの3D Gaussian Splattingの描画手法（というかStatic Mesh化手法）を開発中です。
そちらは年内か年明け早々にでも公開したいと思っていますので、3D Gaussian Splattingにご興味ある方は私か弊社のTwitterアカウントなどチェックしていただければ…！

それではみなさん、よいお年を。

脚注

レイトレースのような「空間」に対する処理を行わずに「頂点」や「表面」に対する処理で済む方法があるので、処理負荷が既存のメッシュ等と同じスケールで済みます ↩︎
ここでは「常にカメラにまっすぐ正対しているペラペラの長方形のメッシュ」という程度の意味です。 ↩︎

背景

3D Gaussian Splattingのデータ表現形式

3D Gaussian Splattingの描画方法

UE5で実装する

0. データのインポート

1. Niagaraで位置テクスチャからパーティクルを生成する

2. Niagaraで画面座標系でのガウス分布を求める

スケール行列S

回転行列R

View行列W

ヤコビ行列J

View空間でのガウス分布の中心座標\vec{x_v}

焦点距離f