Leica DISTO D510の「Error 156: 横方向の傾きが±10°より大きい」について考えてみる
数ヶ月前に手に入れたLeica DISTO D510というレーザ距離計、さまざまな機能がついていて、距離計としての精度も素晴らしく、色々と活用しています。
その機能の一つである、角度計測機能において、Error code156が表示されるトリガーとその挙動について気になったので、改めて色々勉強しなおしたメモ。
Leica DISTO D510について
以下、TAJIMAのWEBカタログより引用
仕様
・規格:国際標準化機構規格ISO16331-1適合品
・インターフェイス:Bluetooth®smart
・レーザー安全基準:クラス2 波長 620~690nm
・標準測定範囲:0.05m~200m
・測定値自動記憶30件
・最小表示値:0.1mm
・標準測定公差:±1.0mm
・防塵・防水性能:IP65
・3年間保証
・画像取扱い:本ウェブサイトページに記載の製品情報および画像の著作権はLeica Geosystems AGに帰属します。
Error 156とは
公式サイトよりError 156については次のように定義してある。
Error 156: 横方向の傾きが±10°より大きい
解決方法: 水平に本体を置きます
ここで、手元にあるD510を水平に床に置き、床の上で上下左右に動かした時、左右に動かした時だけError 156が表示された。
ふと、角度は±10度よりも小さいはずなのにどうしてErrorが表示されるのか気になったので、以下に考えた結果を残しておく。

加速度センサを使った姿勢推定について
まず、D510には加速度センサが内蔵されているという風に仮定した。
こう仮定することによって、加速分だけ誤差が生じている結果、大きな誤差をユーザに表示させないようError 156が機能すると考えた。
また、以下今回の考察の前提条件として、Leica DISTO D510を手に持って操作を行っていると仮定している。
今回座標系を考える上で、センサ座標系を知るためには一度分解をしなければならないが、分解を行うと保証が受けられなくなるため、便宜上、グローバル座標系とセンサ座標系は以下のように仮定する。
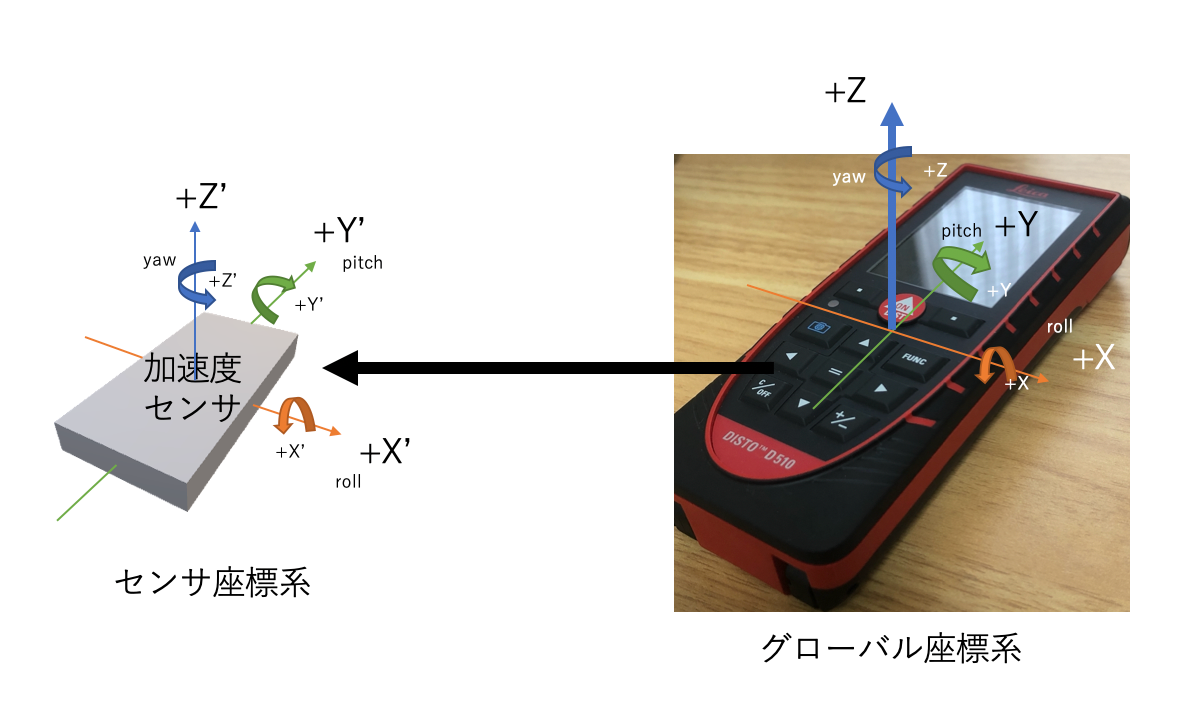
加速度センサ値から加速度を取得し、roll、pitch回転角を算出する。
ここで符号の意味はg[9.80665m/s^2]:重力加速度、a_{hx}[m/s^2],a_{hy}[m/s^2],a_{hz}[m/s^2]:手首周りの各軸加速度、\phi[rad]:roll回転角、\theta[rad]:pitch回転角、\psi[rad]:yaw回転角、\hat\phi[rad]:手首周り加速ありのroll回転角推定値、\hat\theta[rad]:手首周り加速ありのpitch回転角推定値である。
ここでは、センサ座標系のベクトルを(a_x,a_y,a_z)とする。
また、センサ座標系のベクトルをD510の座標系へと回転させるroll、pitch、yawの回転角を\phi,\theta,\psiとする。
これら各ベクトルを行列とみなすと、次式で表すことができる。
R_z(\psi) R_y(\theta) R_x(\phi) \left[
\begin{array}{r}
a_x \\
a_y \\
a_z
\end{array}
\right] = \left[
\begin{array}{r}
a_{hx} \\
a_{hy} \\
g + a_{hz}
\end{array}
\right]
次に、回転行列がもつ直行行列の特性A^{-1}=A^{t}を次式で適用し、展開する。
\left[
\begin{array}{r}
a_x \\
a_y \\
a_z
\end{array}
\right] = R_{x}^{t}(\phi) R_{y}^{t}(\theta) R_{z}^{t}(\psi) \left[
\begin{array}{r}
a_{hx} \\
a_{hy} \\
g + a_{hz}
\end{array}
\right]
= \left[
\begin{array}{r}
\cos\theta \cos\theta a_{hx} + \cos\theta \sin\psi a_{hy} -\sin\theta(g + a_{hz}) \\
(\sin\phi \sin\theta \cos\psi - \sin\psi \cos\phi ) a_{hx} + (\sin\phi \sin\theta \sin\psi + \cos\phi \cos\psi) a_{hy} + \sin\phi \cos\theta (g + a_{hz}) \\
(\cos\phi \sin\theta \cos\psi + \sin\phi \sin\psi) a_{hx} + (\cos\phi \sin\theta \sin\psi - \sin\phi \cos\psi) a_{hy} + \cos\phi \cos\theta (g + a_{hz})
\end{array}
\right]
ここで、姿勢を推定するため(Errorを表示させないために)、手首周りの加速度をa_{hx}=0,a_{hy}=0,a_{hz}=0と仮定し、静止状態で考えると、次式で表すことができる。
\left[
\begin{array}{r}
a_x \\
a_y \\
a_z
\end{array}
\right] = \left[
\begin{array}{r}
-\sin\theta g \\
\sin\phi \cos\theta g \\
\cos\phi \cos\theta g
\end{array}
\right]
以上より、roll回転角\phi[rad]は次式で表す。
\frac{a_y}{a_z} = \frac{\sin\phi\cos\theta g}{\cos\phi\cos\theta g} = \tan \phi
\phi = arctan(\frac{a_y}{a_z})
また、pitch回転角\theta[rad]は次式で表す。
\frac{a_x}{\sqrt{a_{y}^2+a_{z}^2}} = \frac{-\sin\theta g}{\sqrt{(\sin^2 \phi + \cos^2 \phi)\cos^2 \theta g^2}} = -\tan \theta
\theta = arctan(\frac{-a_x}{\sqrt{a_y^2 + a_z^2}})
今回のケースで、手首周りの加速がかかる場合は(a_{hx}\geq 0,a_{hy}\geq 0,a_{hz}\geq 0)、次式で表す。
a_x = \cos\theta \cos\theta a_{hx} + \cos\theta \sin\psi a_{hy} -\sin\theta(g + a_{hz})
a_y = (\sin\phi \sin\theta \cos\psi - \sin\psi \cos\phi ) a_{hx} + (\sin\phi \sin\theta \sin\psi + \cos\phi \cos\psi) a_{hy} + \sin\phi \cos\theta (g + a_{hz})
a_z = (\cos\phi \sin\theta \cos\psi + \sin\phi \sin\psi) a_{hx} + (\cos\phi \sin\theta \sin\psi - \sin\phi \cos\psi) a_{hy} + \cos\phi \cos\theta (g + a_{hz})
\hat\phi = arctan(\frac{a_y}{a_z})
\hat\theta = arctan(\frac{-a_x}{\sqrt{a_y^2 + a_z^2}})
また、算出した各回転角推定値を次式によりラジアンから度へ変換する。
\phi ' = \frac{\hat\phi \cdot{} 180}{\pi}
\theta ' = \frac{\hat\theta \cdot{} 180}{\pi}
以上のことから、a_{hx}\geq 0,a_{hy}\geq 0,a_{hz}\geq 0の場合、その数値が大きくなる度合いで±10度を超える誤差を検出し、左右に揺らすことによってError 156が表示された挙動について理解できた!
ここで、今後この機器を使用する際、注意しなければならない点が、上下に水平移動した場合はError 156は表示されないので、この状態で角度推定すると大きな誤差が発生し、それに対して警告がおこなわれないということを改めて認識できた。


Discussion