全体フロー効率を変えずに価値を出すマジック - リソース効率も交えた考察
この記事の考察をもとに、上位互換にあたる清書した記事を書きました。
↑の記事の方がおすすめです。
概要
色々な仕事の「効率」という事を考えるとき話題になる概念として、リソース効率とフロー効率という2つの概念があります。
これらの概念は、定義から異なるものなのですが、実際にリソース効率を求めた場合にフロー効率は悪くなるのか?という事について、数理モデル的な意味で気になりました。そこで、この記事では
「リソース効率を追求するとフロー効率を良くできないのはどのような場合か」
ということについて定性的に考察します。
...というつもりで書き始めたのですが、全体のフロー効率を変えずに価値を出す方法があるという事に気づいてしまいました。そこで、リソース効率とフロー効率の関係性についての話をしてから、その"マジック"について考察します。
具体的には、以下のとおりです。
- リソース効率とフロー効率は背反的・対立的な概念ではなく、両方の側面で最適な結果はあり得る
- やらなくてよい・無駄なタスクがなく、タスク処理のペースが常に一定の場合、定常状態においてはリソース効率も一定となる
- やらなくてよい・無駄なタスクがある場合には、「広義の生産性」ないし「価値」を最適化するのはリソース効率が最適の場合とは限らない
- タスクの価値がリードタイムに反比例する=フロー効率に比例する場合、全体のフロー効率が一定の条件下でも、フロー効率の平均=単位時間あたりの価値を上げることが可能
- 具体的には、てきとうなタスクを無視すればよい
- アジャイルの文脈でフロー効率を重視するなどと言うとき、実はこの数理現象の事を言っているのでは?
前提
適宜発生するタスクを、1人以上の人が処理していくような状況について考えます。
タスクを処理する人の事をリソースと呼びます。
各リソースは適宜タスクに割り当てられ、タスクは時間を経て消化されていきます。
タスクが発生してから、そのタスクが着手されて完全に消化されるまでの時間をリードタイムと言います。
ここでは、このように時間をかけて決まったリソースでタスクを消化していくようなモデルについて考察します。
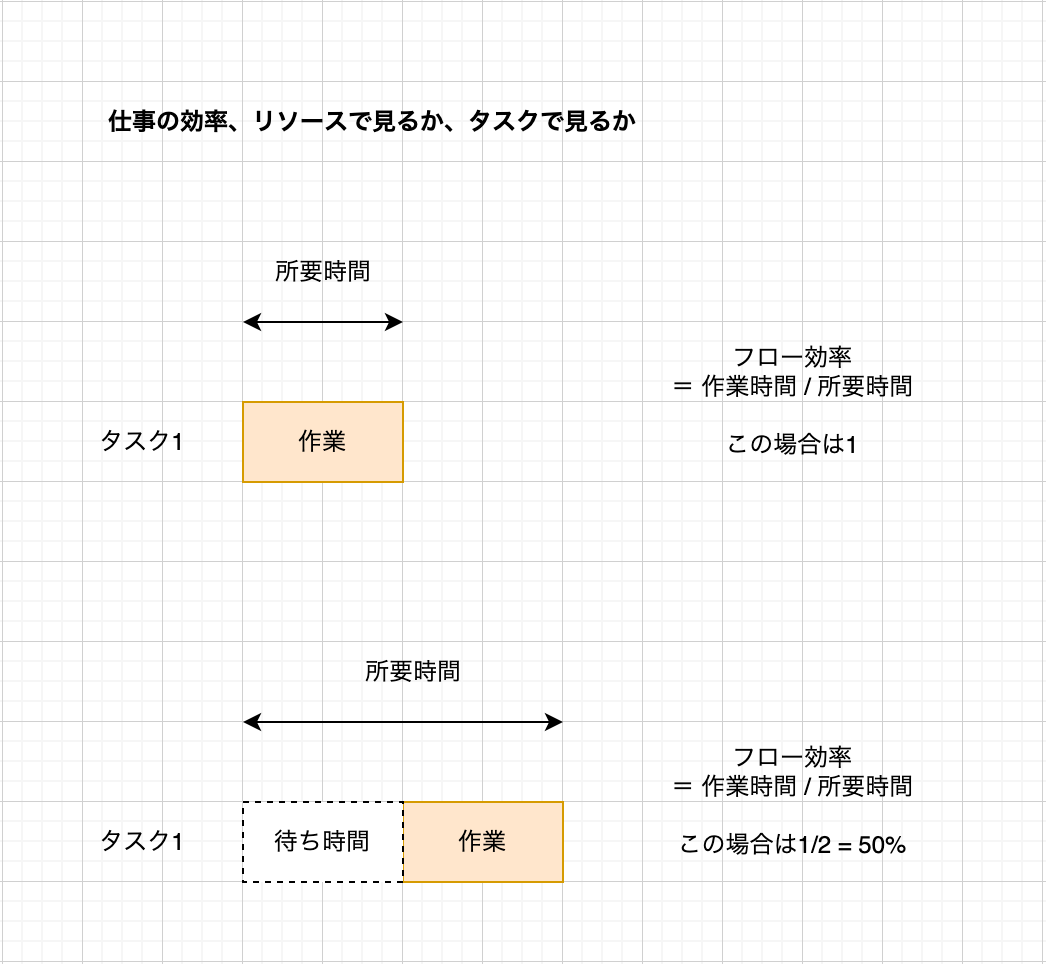
より沢山のタスクを、より短いリードタイムでこなせることが効率の良さという事になりますが、タスクとリードタイムそれぞれの観点で別の効率を定義できます。それがリソース効率とフロー効率です。
リソース効率とは
あるモデルにおいて、各リソースが単位時間に処理できるタスクの平均量のことをリソース効率といいます。
特に、あるリソースについて【稼働しているときは常に同じ作業速度で作業をする】と仮定すると、リソースの稼働率、つまりリソースがタスクに取り組んでいる時間と一致します。
例えば、勤務時間が8時間の人がうち4時間作業していたとすれば、リソース効率は
※この
フロー効率とは
あるモデルにおいて、各タスクの作業量をリードタイムで割った値をフロー効率といいます。
例えば、実作業時間が2時間のタスクについて、タスクの発生から完了までにかかる時間が6時間であったとすれば、そのタスクのフロー効率は
モデルについての考察
リソース効率の最適化とフロー効率の最適化が両立するようなシチュエーション
ここで述べた定義によれば、リソース効率とフロー効率は完全に別の概念ですが、かといって必ずしも相反する概念ではないように思われます。
というのは、もし仕事の量が一定であるとするなら、基本的には各リソースがフル稼働している方が、遊びがない分所要時間も短くなるはずと素朴に考えられるからです。
そこで、常に同じペースでタスクが発生する状況において、このペースを
- 無駄なタスクは存在しない。言い換えると、やらなくてよいタスクはない。
- タスクはいつのタイミングに着手したとしても同じ時間で処理でき、単位時間あたりで生じる成果は同じ。言い換えると、各メンバーの単位時間あたりの仕事量は変わらない。
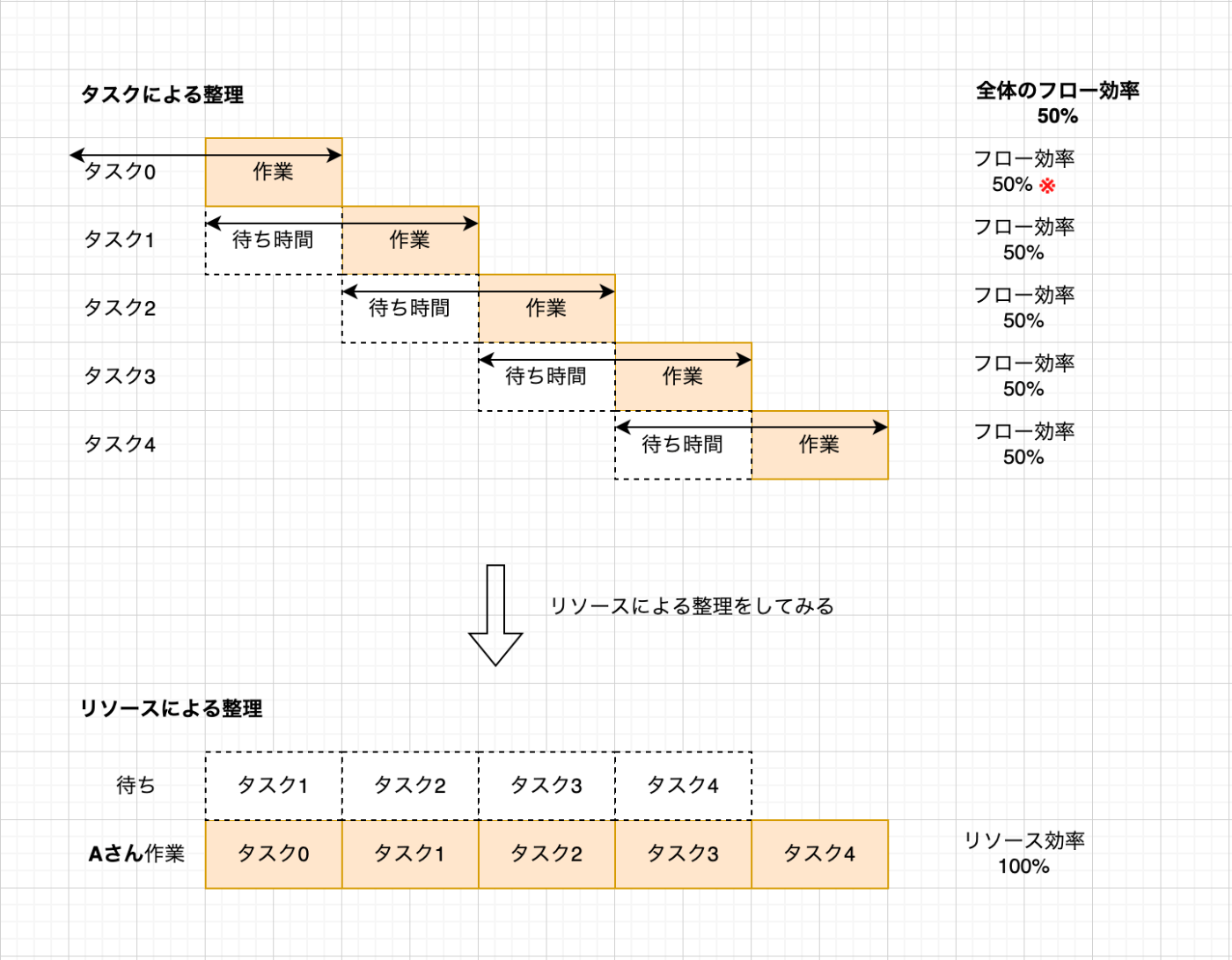
このような条件の状態が定常的に続くと仮定します。このとき、発生したタスクに無駄なタスクはなく、かつ常に同じペースでタスクが湧いてくる事になるので、なんとこの条件ではリソース効率は一意に決まってしまうことになります。上記の仮定を満たす場合には、もはやリソース効率は変数ではなく、定数なのです。リソース人数を
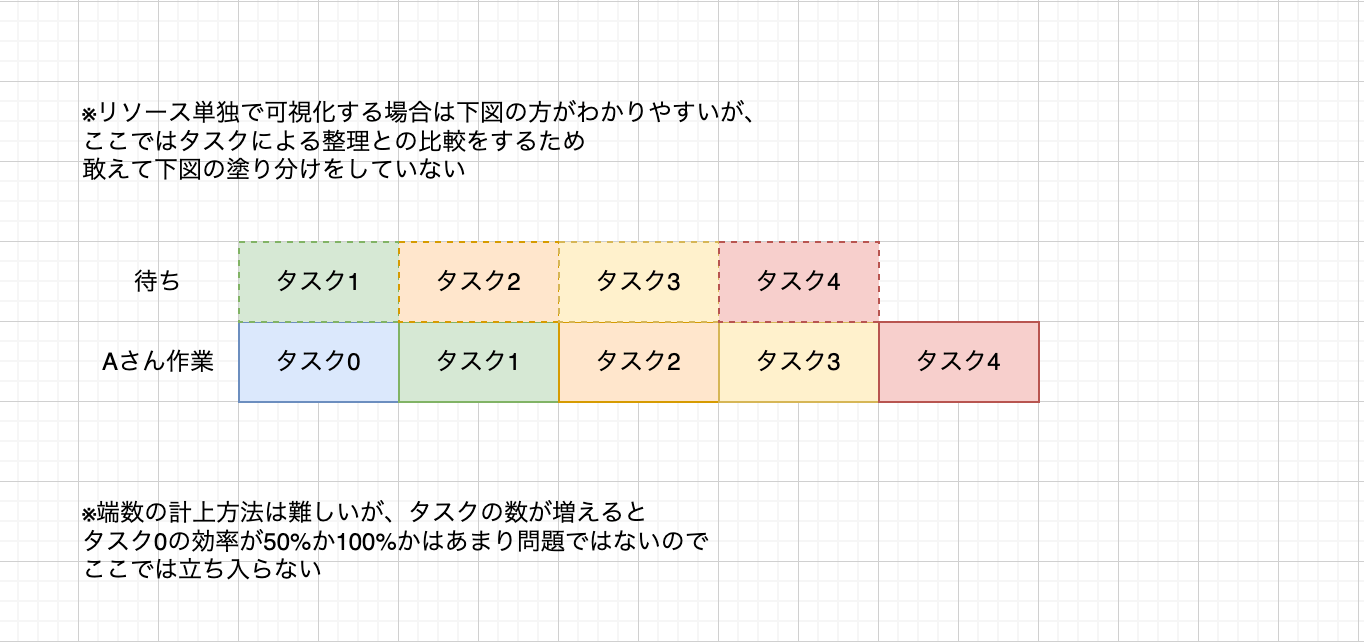
※これは端数やタスクの前後関係などを無視できる場合の話です。細かいタスクの端数や順番を無視できない場合などは微妙な誤差・パズル的な要素が発生しますが、ここではそうした要素は無視できるぐらい小さいものとします。
さて、そうすると、もしフロー効率を最適化する仕事の方法が存在するとしても、上記の仮定を満たす限りはそのような仕事の方法もまたリソース効率が最大(一定)なのであって、リソース効率とフロー効率の"トレードオフ"のような事は発生しなくなります。
リソース効率の最適化とフロー効率の最適化が両立しないシチュエーション
そこで、仮にリソース効率とフロー効率の"両取り"ができないようなシチュエーションが存在するとしたら、以下の少なくとも1つが成立する、という事になります。
- やらなくてよいタスクが存在する。
- 各メンバーの単位時間あたりの仕事量が変わる。タスク自体を処理する速度か、単位時間あたりで生じる成果の少なくとも片方は変化する。
ここでは、定性的にそれぞれの例を考えてみましょう。
- もし「やらなくてよいタスク」が存在するとしたら、そのようなタスクを"効率的に"実施するリソース効率最適なモデルは、実際の価値の提供という点においてフロー効率なモデルに劣る可能性があります。
- もしフロー効率で最適なモデルで「タスク自体を処理する速度」が向上したり、あるいは早く価値を届ける・機能をリリースする事によって生じる成果がレバレッジ的に増えるならば、常にリソースが埋まっているがフロー効率的によくないモデルよりも結果的に"生産性"が高くなる可能性があります。ここでいう生産性は、必ずしも単位時間あたりの作業実績という事に限らず、成果を加味した生産性、「広義の生産性」とでもいうような意味です。
このような場合には、リソース効率
つまり、実際にはやらなくてよいタスクが存在するし、またタイミングによって生じる成果・価値も変わるし、それまでの積み重ねや状況によってタスク自体を処理する速度も変わるので、見かけのリソース効率が悪いように見えても広義の生産性は上がる場合がある、ということです。
やらなくてよいタスクを見抜くことは平均フロー効率とは関係ないが、フロー効率の平均には影響する
ここで、早く機能をリリースした方がレバレッジ的な価値を持つという現象は確かにフロー効率の概念と密接に関係しています。フロー効率を高くすれば、早くリリースができ、より高い価値が生じるという理屈です。
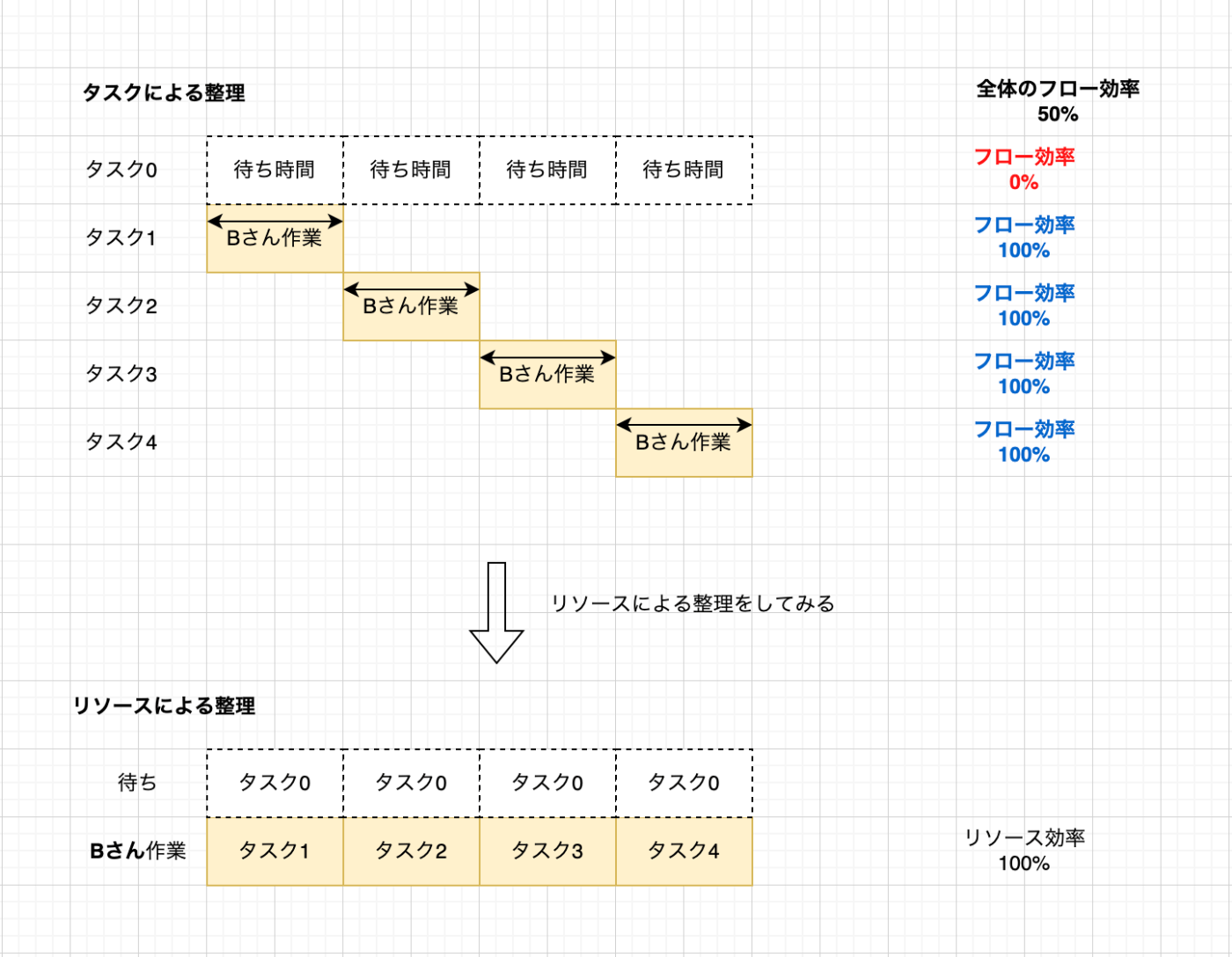
しかし、やらなくてよいタスクを見抜くことは全体のフロー効率(いわゆる平均フロー効率)とは関係がありません。実際、もしフル稼働している状態で、あるタスクをずっとやらなかったとしたら、そのタスクに関するリードタイムは増え続けることになり、フル稼働している前提ではリードタイムの平均は変わることがないので、その意味で全体のフロー効率は一定のままです(具体的な計算については後述します)。
しかし、言葉遊びみたいですが、フロー効率の平均はなんと適当に無視するタスクを作るだけでも効率的に上げる事ができます。
「時は金なり」成果がフロー効率に比例するモデルの場合
世の中には様々な成果がありますが、ここで一つ一つのタスクの成果がリードタイムに反比例する、つまりフロー効率に比例するものとして考えてみます。(もちろん、このような条件に当てはまらない成果も多くあると思いますが、早期のリリースが望まれるような機能については当てはまる場合もあるかと思います。)
この条件で、
このとき、時刻
では、
そうすると、
私はこれにびっくりしてしまったのですが、なんと、最初にひとつ溢れているタスクが存在しているだけで、未来永劫ずっと効率が
では、
答えは簡単で、フロー効率は
これ、めちゃくちゃすごくないですか??私はびっくりしてしまいました。
ところで、同じ条件で、
そうすると...滞留していたタスクが1つあったとすると、
ここで、最初のタスクのリードタイムは増え続けていて、
しかし、成果は違います。単位時間あたりの成果は、各タスクのフロー効率の平均なので、つまり
なんと、無視するタスクを作ることによって、成果が
これは最初に滞留しているタスクが
アジャイル等の文脈で「フロー効率を重視する」という事の本当の意味はこういう事ではないか?と私は考えています。つまり、全体で漏らさずタスクを順番にこなすという事ではなくて、処理可能な量を維持しながらリードタイムを少なくすることによって、全体ではなくて個々のタスクのリードタイムをへらすことができ、それによって成果がフロー効率に比例する場合にはより成果を上げられるようになる、という事です。
まとめ
- リソース効率とフロー効率は背反的・対立的な概念ではなく、両方の側面で最適な結果はあり得る
- やらなくてよい・無駄なタスクがなく、タスク処理のペースが常に一定の場合、定常状態においてはリソース効率も一定となる
- やらなくてよい・無駄なタスクがある場合には、「広義の生産性」ないし「価値」を最適化するのはリソース効率が最適の場合とは限らない
- タスクの価値がリードタイムに反比例する=フロー効率に比例する場合、全体のフロー効率が一定の条件下でも、フロー効率の平均=単位時間あたりの価値を上げることが可能
- 具体的には、てきとうなタスクを無視すればよい
- アジャイルの文脈でフロー効率を重視するなどと言うとき、実はこの数理現象の事を言っているのでは?
おまけ
タスクを無視するなんて...!?と思った方は、次の画像を思い出してください。
特定のタスクを完全に無視するのではなくて、先延ばしにしているだけなのです。
この記事の前半部分、定常状態においてはリソース効率が一定となるという辺りの話は、以前から書きたいと思っていました。
というのは、
例えば、勤務時間が8時間の人がうち4時間作業していたとすれば、リソース効率は
です。 4/8=1/2
この話を敢えて途中に書いたのですが、普通の作業者についてリソース効率が
多くの場合、目の前の開発には(休憩が必要ならば休憩も総時間としてカウントした上で)常にリソース効率
フロー効率を求めるにあたって、必ずしもリソース効率の意味で最適でなくなるというのはそのとおりですが、かといってリソース効率が
それを踏まえて、この記事では効率の両取りができないシチュエーションについて考察していたのですが、その仮定について考える中で、「平均フロー効率」と「フロー効率の平均」は異なる概念だという事に気づき、「フロー効率最適と言っている事の本当の意味はこれではないのか!?」と思って、そのまま勢いで書きました。
おかしなところや気になるところがあれば、ぜひコメントください。


Discussion
私の頭の中にあったけど、描いてなかった図をかきましたわ