統計的確率(超基礎)
統計的確率と確率分布1
こんにちは!わいわわです。
今回は統計的確率と確率分布について学習していきます!
確率
統計的な確率とは?さいころを振る例を用いてみていきます。
サイコロは1-6までのいずれかの芽が出ます。
ということは、サイコロの出る目は6通りで、
それぞれの目は6つに1つの割合で出ることになります。
この割合が確率です。
- 「サイコロを振る」という行為を試行
- サイコロの出る目の全て(1~6)を標本空間
- 「目が出る」を事象
とそれぞれ呼びます。
確率は[事象Eの起こる場合の数/起こりうるすべての場合の数]
で表すことができます。
確率変数が起こりうる値のことを実現値と呼び、
サイコロの場合だと確率変数xの実現値は[1,2,3,4,5,6]になります。
このように実現値が数え上げられるときは離散確率変数と呼び、
そうでないときは連続確率変数と呼びます。
この数え上げられるというのは「連続ではない飛び飛びの値をとる」ということで、
サイコロの実現値のように有限個のこともあれば無限の場合もあります。
離散と連続の違い
離散は「離れ離れになること」を意味します。
例としてはサイコロの目や人の数、車の台数などがあります。
一方、連続とは「続いている」ことを意味します。
例としては身長や体重、温度、速度などは連続的なデータだといえます。
サイコロもつながっているじゃん!ということではなく、「続いている」とは
身長や体重のように厳密に図ろうとすればcmからmm、さらにnmのような
小さい単位を用いることで、理論的にはいくらでも細かく測定できる、ということです。
一様分布
先述のサイコロの例のように、「すべての事象の起こる確率が等しい」
というデータ分布を一様分布と呼びます。
一様分布がどのようなものか、サイコロを1000回ふるシミュレーションを実施します。
import numpy as np
import matplotlib.pyplot as plt
# サイコロの目
dice = np.array([1, 2, 3, 4, 5, 6])
# サイコロを振る回数(試行回数)
steps = 1000
# サイコロの目(1~6)からランダムにstepsの数だけ抽出する
dice_rolls = np.random.choice(dice, steps)
# 1~6の目が出た割合(確率)を格納する配列
prob = np.array([])
# 1~6の目が出た割合を出現確率としてratioに順次格納する
for i in range(1, 7):
prob = np.append(
prob,
# サイコロのiの目が出た回数を試行回数で割って出現確率を求める
len(dice_rolls[dice_rolls == i]) / steps
)
# x軸をサイコロの目(1~6)、y軸を出現確率にして棒グラフを描画
plt.bar(dice, prob)
plt.grid(True)
plt.show()
!出力結果!

nm.random.choice()関数を使用し、サイコロを振るシミュレーションを行っています。
これは第一引数に抽出対象の値、第二引数に抽出回数を指定すると
指定した回数にランダムに抽出が行われ、抽出された値が配列で返されます。
それを今回/steps、同じ数で割って確率を求めています。
バラツキは若干ある、、、ものの、1/6に近い数字にそれぞれなっています。
これを1万回、10万回と増やしていくと、1/6により近づくようになります。
また、確率変数xが離散である場合、離散型一様分布と呼びます。
二項分布
例)コインを投げた時に表が出るか裏が出るか
のように、何かを行ったときにおこる結果が2つしかない試行のことを
ベルヌーイ試行といいます。
ベルヌーイ試行は2つの結果のうち、一方を「成功」として確率変数がとる値を「1」、
もう一方の結果を「失敗」として確率変数がとる値を「0」とします。
また、何回も試行することを反復試行といいます。
scipy.stats.binom.pmf()関数
上記の関数を使用すると確率を求めることができます。
from scipy.stats import binom
binom.pmf(3, 10, 1/6)
出力結果→0.1550453595742519
インポートしたのち、
binom.pmf(3,10,1/6)
「1/6を10回おこなって、1/6が3回でる確率」という意味になります。
今度は反復試行の回数を10回にして、特定の目が出る回数0~10回ごとの確率を求め、
結果をグラフにしてみます。
import numpy as np
import matplotlib.pyplot as plt
# 反復試行の回数
n = 10
# 特定の目が出る確率
p = 1 / 6
# 確率変数が取る成功回数(特定の目が出る回数)を配列に格納
k = np.arange(0, n)
# 特定の目が出る回数ごとの確率P(X=k)を求める
pk = binom.pmf(k, n, p)
# P(X=k)を出力
print(pk)
# 横軸に特定の目が出る回数、縦軸に確率にして棒グラフにする
plt.bar(k, pk)
plt.show()
!出力結果!
0.1550453595742519
[1.61505583e-01 3.23011166e-01 2.90710049e-01 1.55045360e-01
5.42658759e-02 1.30238102e-02 2.17063503e-03 2.48072575e-04
1.86054431e-05 8.26908584e-07]
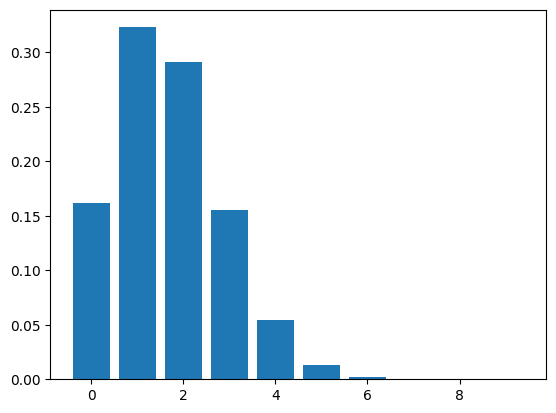
さらに反復試行の回数を10回、20回、50回と増やして表にします。
# サイコロを投げる(反復試行の)回数のリスト
roll = [10, 20, 50]
# 特定の目が出る回数の確率を反復試行の回数ごとにグラフにする
for n in roll:
# 確率変数が取る成功回数(特定の目が出る回数)を配列に格納
k = np.arange(0, n+1)
# P(X=k)を求める
pk = binom.pmf(k, n, p)
# 反復試行の回数ごとにグラフを描画
plt.plot(
k, pk,
marker="o",
label="n={}".format(n))
# グラフを見やすくするためx軸(成功回数)の上限を20にする
plt.xlim(0, 20)
# 凡例を表示
plt.legend()
# グラフを出力
plt.show()
!出力結果!

反復試行の回数の増加に従って、
離散型二項分布の確率質量関数が出力する値の分布の幅が右側にずれます。
また、動じぬ分布の形が左右対称の山の形に近づいていることもわかります。
このような左右対称の山の形をした分布を正規分布と呼びます。
正規分布は二項分布の極限状態だということをラプラスの定義と呼び、
統計学の区間推定などに応用されています。
所感
今日は統計の中の確率と一部の確率分布をまとめました。
サイコロだったのでわかりやすかったですが、実データになると
すごく複雑になっていくんだろうなと思います。
確率分布はまだ正規分布があるので、明日、まとめていきます!

Discussion