論文
前回は、S4の関連派生モデルであるS4Dについて解説しました。
今回は、少し脇道にそれます。というのも、MambaとS4(S4D)は同じ著者ですが、本論文は著者が違うからです。しかし、Mambaの論文で一部言及される箇所があるため、解説する事にしました。
タイトル
Hungry Hungry Hippos: Towards Language Modeling with State Space Models
論文: https://arxiv.org/pdf/2212.14052
Github: https://github.com/HazyResearch/H3
解説ステップ
概要
- SSM に Linear Attention の発想を取り入れた
- Shift-SSM と Diagonal-SSM の二段構え
- Induction Head Task と Associative Recall Task を解決できる
- 精度はS4Dと肉薄。計算はH3が速い
何が問題だったか
S4では、以下の記憶に関するタスクが苦手とされています。

- Induction Head Task
特定のトークンの直後の文字を当てるタスクです。表では abcde├fghi...xyz├ という INPUT になっており、最後のトークンである ├ が質問文のようなもので、これの直後の記号を当てろという事で、答えは f です。
- Associative Recall Task
辞書型のような key-value で格納されている key に対しての value を当てるというタスクです。INPUT a2c4b3d1a に対して、a が質問文のようなもので、2 が答えです。
どう解決したか
Shift and Diagonal SSM を使う事で、それらを解決。
※S4がキレイに理論派生であるのに対して、H3はなんかNN特有の「気持ちで解決」という色が強いという印象...
H3 Layer
H3は以下のような、Transformerに見られる Query-Key-Value への変形と、 Shift-SSM と Diagonal-SSM を組み合わせた構造をしています。

Linear Attention
H3 Layer はこの Linear Attention から着想を得て、一部をSSMに置き換えたものです。なのでまずはこの Linear Attention について解説します。
まず、Transformer で使われている Softmax Attention の形式は以下です。
\begin{aligned}
y_t &= \sum_{s ( \leq t)} softmax(Q_t K_s^T) V_s \\
&= \frac{\sum_{s ( \leq t)} \exp{(Q_t K_s^T)} V_s}{\sum_{s ( \leq t)} \exp{(Q_t K_s^T)}}
\end{aligned}
Q_t \in \mathbb{R}^{1 \times d}, \ K_s^T \in \mathbb{R}^{d \times 1}, \ V_s \in \mathbb{R}^{1 \times d}, \ y_t \in \mathbb{R}^{1 \times d}
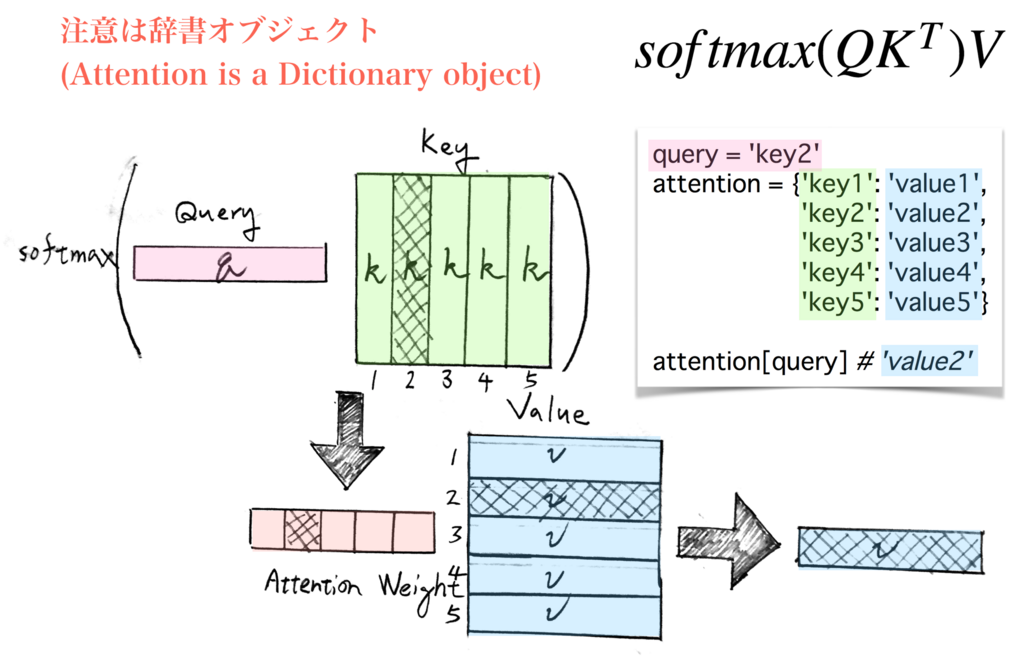
こちらを引用
この \exp{(Q_t K_s^T)} を 特徴写像\phi(.)を使って、\phi (Q_t) {\phi(K_s)}^T のように書けるとします。そうすると
y_t \approx \frac{\sum_{s ( \leq t)} \left( \phi (Q_t) {\phi(K_s)}^T \right) V_s}{\sum_{s ( \leq t)} \phi (Q_t) {\phi(K_s)}^T } = \frac{\phi (Q_t) \sum_{s ( \leq t)} {\phi(K_s)}^T V_s}{\phi (Q_t) \sum_{s ( \leq t)} {\phi(K_s)}^T }
のように変形でき
\begin{aligned}
S_t & \colonequals \sum_{s ( \leq t)} {\phi(K_s)}^T V_s \ \ \ \in \mathbb{R}^{d\times d} \\
z_t & \colonequals \sum_{s ( \leq t)} {\phi(K_s)} \ \ \ \in \mathbb{R}^{1 \times d}
\end{aligned}
のように定義すると
y_t \approx \frac{\phi (Q_t) S_t}{\phi (Q_t) z_t^T}=\frac{\phi (Q_t) S_t}{d_t}
です。d_tはスカラーです。また、以下のような漸化式を得ます。
S_t=S_{t-1}+{\phi(K_t)}^TV_t, \ \ \ z_t=z_{t-1}+{\phi(K_t)}^T
H3では、この \phi(K) を Shift-SSM に、 \sum を Diagonal-SSM に見立てた構造を取っています。
y=Q \left( SSM_{diag} ( SSM_{shift}(K) V) \right) \in \mathbb{R}^{1 \times d}
※ SSM_{shift}(K) V \in \mathbb{R}^{d \times d}
各構造の「気持ち」
結局のところ、このH3の構造はAttentionを変形したものであり、本質的にはAttentionと同等の事をしています。
つまり、入力uに対して別々の重みW_Q,W_K,W_Vをかけて Query, Key, Value を構成し、Query によって適切な比重で構成された Value' を取り出すような仕組みです。
その上で、敢えて、各構造の気持ちを書いてみると以下のような感じになると思われます。
-
SSM_{shift}(K)=K'
後の解説でも見られますが、SSM_{shift} は時系列次元への1次元畳み込みと同質のものです。つまり、ここでは直近のKeyをフィルターによって抜き出して要約したような Key' を作成します。
-
K'V \in \mathbb{R}^{d \times d}
K'という Key で V を埋め込んで保管しています。この操作が何故そういうイメージになるかは以下を参照してください。
K'Vのイメージ
K' が (0, 0, 1) のベクトルで、Vが(0.7, 0.2, 0.1) だったとしましょう。このとき
{K'}^T V=
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0.7 & 0.2 & 0.1 \\
\end{bmatrix}
ここで Q が (0, 1, 0) などのように直行していれば、Q{K'}^T V=(0, 0, 0) となって V の値は取り出せません。Vを取り出すには、QがK'と近い(つまり内積が~1)ようなベクトル(0, 0, 1)のような時だけです。
よって、{K'}^T Vといった行列は、VをK'で埋め込んで保管したような行列、のイメージになります。
-
SSM_{diag}(K'V)=(K'V)'
SSMは畳み込み形式で表せます。つまり、より長期なフィルター(カーネル)による入力K'Vを s<tの時間点に対して抜き出して要約したようなものです。(K'V)' でできます。
-
Q(K'V)'
Query によって適切な比重で構成された Value' を取り出すような操作です。
全体としては、S4D で見られる長時系列点でのカーネルの減衰K_L=C{\={A}}^{L-1}\={B} を防ぐ意味で、初段のSSM_{shift}によって、過去の情報を直近に保持するような操作を行い、カーネルの減衰による過去情報の消失を防いでいる、意味合いがあります。
Shift-SSM
入力uの次元D_{in}=2, 内部状態xの次元D_x=4, 出力yのD_{out}=2, 入力uの時系列長Lの場合
\vec{u_0}=\begin{bmatrix}
u_{00} \\ u_{01}
\end{bmatrix}, \ ... \ , \ \
\vec{u_t}=\begin{bmatrix}
u_{t0} \\ u_{t1}
\end{bmatrix}, \ ... \ , \ \
\vec{u_L}=\begin{bmatrix}
u_{L0} \\ u_{L1}
\end{bmatrix}
\begin{bmatrix}
\vec{x}_{t}^{(0)} \\
\vec{x}_{t}^{(1)} \\
\vec{x}_{t}^{(2)} \\
\vec{x}_{t}^{(3)} \\
\end{bmatrix}=
\underbrace{
\begin{bmatrix}
0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
}_{A}
\begin{bmatrix}
\vec{x}_{t-1}^{(0)} \\
\vec{x}_{t-1}^{(1)} \\
\vec{x}_{t-1}^{(2)} \\
\vec{x}_{t-1}^{(3)} \\
\end{bmatrix} +
\underbrace{
\begin{bmatrix}
1 \\
0 \\
0 \\
0 \\
\end{bmatrix}
}_{B}
\vec{u_t}
\vec{y}_t=
\underbrace{
\begin{bmatrix}
c_{0} & c_{1} & c_{2} & c_{3}
\end{bmatrix}
}_{C}
\begin{bmatrix}
\vec{x}_{t}^{(0)} \\
\vec{x}_{t}^{(1)} \\
\vec{x}_{t}^{(2)} \\
\vec{x}_{t}^{(3)} \\
\end{bmatrix}
書き下すと上のような行列になっている。このとき、入力はベクトルであり、行列演算による内積は取らない事に注意してほしい。
t=0~3 までの変化を見てみよう。
t=0の時
\begin{bmatrix}
\vec{x}_{0}^{(0)} \\
\vec{x}_{0}^{(1)} \\
\vec{x}_{0}^{(2)} \\
\vec{x}_{0}^{(3)} \\
\end{bmatrix}=
\begin{bmatrix}
0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
\vec{0} \\
\vec{0} \\
\vec{0} \\
\vec{0} \\
\end{bmatrix} +
\begin{bmatrix}
1 \\
0 \\
0 \\
0 \\
\end{bmatrix}
\vec{u_0}=
\begin{bmatrix}
\vec{u_0} \\
\vec{0} \\
\vec{0} \\
\vec{0} \\
\end{bmatrix}
,\ \ \ \
\vec{y_0}=c_0 \vec{u_0} + c_1 \vec{0} + c_2 \vec{0} + c_3 \vec{0}
t=1の時
\begin{bmatrix}
\vec{x}_{1}^{(0)} \\
\vec{x}_{1}^{(1)} \\
\vec{x}_{1}^{(2)} \\
\vec{x}_{1}^{(3)} \\
\end{bmatrix}=
\begin{bmatrix}
0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
\vec{u_0} \\
\vec{0} \\
\vec{0} \\
\vec{0} \\
\end{bmatrix} +
\begin{bmatrix}
1 \\
0 \\
0 \\
0 \\
\end{bmatrix}
\vec{u_1}=
\begin{bmatrix}
\vec{u_1} \\
\vec{u_0} \\
\vec{0} \\
\vec{0} \\
\end{bmatrix}
,\ \ \ \
\vec{y_1}=c_0 \vec{u_1} + c_1 \vec{u_0} + c_2 \vec{0} + c_3 \vec{0}
t=3の時
\begin{bmatrix}
\vec{x}_{3}^{(0)} \\
\vec{x}_{3}^{(1)} \\
\vec{x}_{3}^{(2)} \\
\vec{x}_{3}^{(3)} \\
\end{bmatrix}=
\begin{bmatrix}
0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
\vec{u_2} \\
\vec{u_1} \\
\vec{u_0} \\
\vec{0} \\
\end{bmatrix} +
\begin{bmatrix}
1 \\
0 \\
0 \\
0 \\
\end{bmatrix}
\vec{u_3}=
\begin{bmatrix}
\vec{u_3} \\
\vec{u_2} \\
\vec{u_1} \\
\vec{u_0} \\
\end{bmatrix}
,\ \ \ \
\vec{y_3}=c_0 \vec{u_3} + c_1 \vec{u_2} + c_2 \vec{u_1} + c_3 \vec{u_0}
となり、B=\vec{e_1}のときは、ShiftSSM の操作は、時系列次元への、重さ\vec{C}1次元畳み込みと同等となります。

Diagonal-SSM
S4D と同等のため割愛します。
疑似コード

FlashConv という概念が、このH3論文で登場しますが、それはあくまで FFT, 要素積, iFFT の高速化であって、モデル構造自体の本質ではありません。つまり S4 同様、y=IFFT(FFT(K) \cdot FFT(u)) が計算の本質であり、それが理解できるのであれば、この疑似コードは特に問題にならないでしょう。
唯一、Transformer 同様 multi head の概念を取り入れている事に注意します。SSM_{shift}(K) の後に head 毎に分割し、共通のSSM_{diag} に入力しています。
https://github.com/HazyResearch/H3/blob/5c4d06b5795405170387c80998b58d76179a8a1a/src/models/ssm/h3.py#L61-L65
self.kernel が SSM_{diag} で、self.H = d_model // head_dim の次元で1つだけ(つまりヘッドに渡って共通のインスタンスで)初期化されている事が分かります。
結果
H3 Hybrid (GPTをベースとした一部の層以外をH3構造に置き換えたモデル)という謎のモデルで結果を測定しており(なぜ Transformer を踏襲しているのか…)、よくわからないのでメイン結果は飛ばします。
Our hybrid model simply retains two self-attention layers: one in the second layer, and one in the middle (layer 2 + N/2 for an N-layer model, N even)
The Long Range Arena (LRA)
S4D と比較すると、長時系列の予測で結果は肉薄しており、計算効率の観点でH3が優秀と結論付けています。

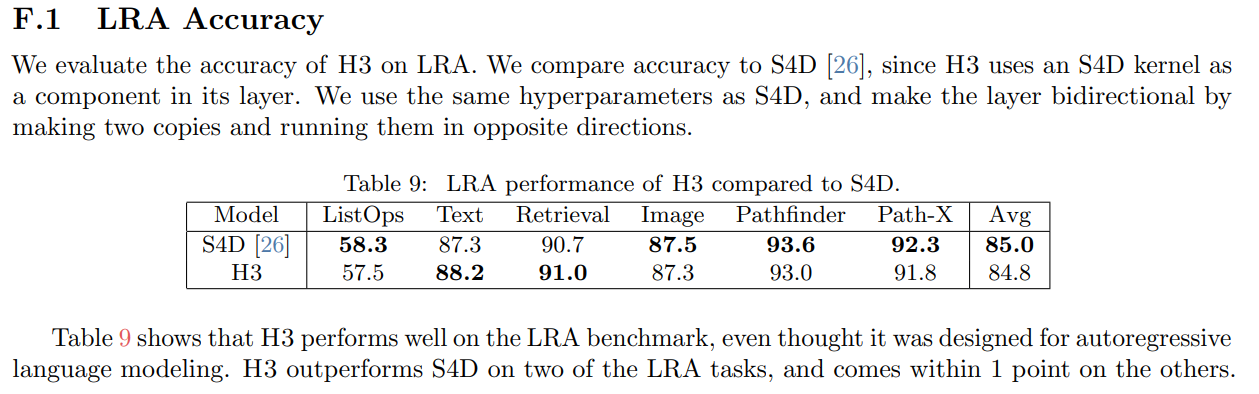







Discussion