📚

5th Kibo-RPCに参加した話

2024/10/30に公開

kiborpc

tech

※読む人のこと考えてないほぼ殴り書きの記事なので容赦下さい．．．

謝辞

Kibo-RPCプログラムに参加できたことをこの場を借りて深く感謝申し上げます．プログラムの開催を可能にしてくださった主催者の皆様、関係者の皆様に心からの敬意と感謝の意を表します．

I am honored to have had the opportunity to participate in the Kibo-RPC program. I would like to express my deepest gratitude to the organizers and all the individuals involved who made this program possible.

概要

2024年Kibo-RPCにCelestial-Ravensとして参加しました．にひにひはAstrobeeの移動系の部分を担当しました．

Kibo-RPCとは↓

実績

予選1位通過(日本代表として決勝出場)

ミッション内容

astrobeeというロボットが，Kiboの壁に貼ってあるアイテムが印刷された紙を画像認識しながら巡回し，宇宙飛行士が出題したアイテムの近くまで行き，撮影をするというミッションです．アイテムはランダムで，複数個あったり，重なってたり，サイズがバラバラだったりします．

巡回->宇宙飛行士が出題する紙を画像認識->そのアイテムの場所まで行く

という流れです．また，Kibo内には立ち入り禁止区域，壁との一定距離の確保が必須とされていて，違反するようなコードになっていると，実行されないようになっています．

にひにひの役割

にひの担当箇所は主に移動系でした．以下のことが要求されていました．

astrobeeを目標まで確実に移動させる
紙の向きに合わせて姿勢を制御する
紙に印刷されたアイテムをきれい撮影できる位置を計算

にひにひがチームメンバーとして心掛けたこと

いままでロケットサークルで学んだマネジメントを生かそうと以下のことを心掛けました．

報告を早くすること
早く取り組むこと
チーム締め切り-2,3dayをベースに予定を立て，少しでも遅れそうなときはリーダーに報告すること
大きい目標，中くらいの目標，小さい目標をたてて，モチベと進捗管理をしっかりすることを意識すること

開発にあたり注意したこと

担当箇所全体について

移動，姿勢を扱う上で，何を基準にした値なのかを的確に整理する必要があります．具体的には

Kibo内の絶対座標(moveTo()はこれをもとにしています)
astrobeeのフロントカメラから見た座標・姿勢
astrobeeのリアカメラから見た座標・姿勢
astrobeeの体積中心から見た座標・姿勢
紙(ARマーカ)から見た座標・姿勢

があります．わけわからんくならないために，変数名には特に気をつかいました．

今回は"どこの座標系でみたとき"，"どこから"，"どこまで"，"ベクトルorクオータニオン"を各"_"で区切った変数名を決定しました．

例えば，"ASTROBEEの体積中心から見た座標系"で，"ARマーカ"から"紙の中心位置"を表す"ベクトル"の変数は

"papercenter_ar_ASTROBEE_Pvec"

というように命名しました．

移動について

astrobeeはmoveTo()というあらかじめ用意された関数に座標と姿勢を渡してあげるとそれ通りに移動してくれるようになっています．しかし，moveTo()関数は実行が完了するまで割り込みで中断させたり，途中で座標と姿勢を変更することができません．つまり，タイムロスを避けるためには一発で目的の座標と姿勢をmoveTo()を渡してあげる必要があります．また，astrobeeの特性上最小移動角度，距離が決まっています．

つまり，

巡回時と同様に大雑把な座標まで行く
画像認識
補正するように移動
といったプロセスでは時間ロスが大きすぎる，最小移動距離，角度の制限上不可能という欠点があります．

故に

巡回時に最適位置・姿勢を計算
計算した位置に移動
というようにしました．

姿勢について

アイテムが書かれている紙にはARマーカがついていて，そのマーカまでの距離，マーカの姿勢をもとに最適撮影姿勢を計算しました．

ARマーカのクォータニオン，座標はastrobeeから見たもので，他の担当箇所から引数としてもらいます．

運営で用意されている関数(抜粋)

moveTo()
- 指定した絶対座標の位置，姿勢に移動する関数です．割り込み等ができないので，これを実行中の時は同じスレッドでほかの処理ができません
getKinematics
- この関数を呼ぶことによって現在の位置，姿勢を絶対座標で入手できます
Types
- Position
  - 座標を扱ういわゆるdoubleのVector3です.
- Quaternion
  - 姿勢を扱ういわゆるfloatのVector4，クオータニオンです．

Quaternionについての基礎知識

Quaternionの知識がほぼなかったので，「3DCGプロログラマーのためのクォータニオン入門　四訂版　金谷一郎　工学社」を読んで勉強しました．

Quaternionとは，
$x$ , $y$ , $z$ を回転軸とし $w$ 回転軸まわりに回転させたもの

Q=xi+yj+zk+w

ここで，

i

j

k

は虚数単位である．この虚数どうしの関係等々いろいろお話はあるが，いったん省略する．

Quaternionの共役

普通の複素数のように共役複素数がある．

\overline{Q}=-xi-yj-zk+w

Quaternionの掛け算

Quaternion $Q_1$ と $Q_2$ の掛け算はハミルトン積で以下のようになる

Q_1Q_2 = \begin{pmatrix} w_1 & -z_1 & y_1 & x_1 \\ z_1 & w_1 & -x_1 & y_1 \\ -y_1 & x_1 & w_1 & z_1 \\ -x_1 & -y_1 & -z_1 & w_1 \end{pmatrix} \begin{pmatrix} x_2\\ y_2\\ z_2\\ w_2 \end{pmatrix}

private Quaternion QuaternionMultiplication(Quaternion _q1, Quaternion _q2) {
        float[][] q1_matrix = new float[4][4];
        float[][] q2_matrix = new float[4][1];
        q1_matrix[0][0] = _q1.getW();
        q1_matrix[1][0] = _q1.getZ();
        q1_matrix[2][0] = -_q1.getY();
        q1_matrix[3][0] = -_q1.getX();
        q1_matrix[0][1] = -_q1.getZ();
        q1_matrix[1][1] = _q1.getW();
        q1_matrix[2][1] = _q1.getX();
        q1_matrix[3][1] = -_q1.getY();
        q1_matrix[0][2] = _q1.getY();
        q1_matrix[1][2] = -_q1.getX();
        q1_matrix[2][2] = _q1.getW();
        q1_matrix[3][2] = -_q1.getZ();
        q1_matrix[0][3] = _q1.getX();
        q1_matrix[1][3] = _q1.getY();
        q1_matrix[2][3] = _q1.getZ();
        q1_matrix[3][3] = _q1.getW();

        q2_matrix[0][0] = _q2.getX();
        q2_matrix[1][0] = _q2.getY();
        q2_matrix[2][0] = _q2.getZ();
        q2_matrix[3][0] = _q2.getW();

        float[][] result_matrix = new float[4][1];
        for (int i = 0; i < 4; i++) {
            result_matrix[i][0] = 0;
            for (int j = 0; j < 4; j++) {
                result_matrix[i][0] += q1_matrix[i][j] * q2_matrix[j][0];
            }
        }
        return new Quaternion(result_matrix[0][0], result_matrix[1][0], result_matrix[2][0], result_matrix[3][0]);
    }

回転Quaternionによる姿勢Quaternionの回転

例えば，姿勢Quaternionの $Q_2$ を $Q_1$ 回転させる場合，回転後のQuaternionを $Q_3$ とすると

Q_3=\overline{Q_1}Q_2Q_1

と表される

回転Quaternionによるベクトルの回転

回転させるものが
$$
v_1=\begin{pmatrix}
v_x\
v_y\
v_z
\end{pmatrix}
$$

である場合

ベクトルをQuaternionに変換
$$Q_2=\begin{pmatrix}
v_x\
v_y\
v_z\
0
\end{pmatrix}$$
$Q_1$ と $Q_2$ と $\overline{Q_1}$ の掛け算

$Q_3=\overline{Q_1}Q_2Q_1$
実部を無視して虚部だけを取り出す

こうすることでベクトルをQuaternionで回転させることができる．

回転ベクトルを回転Quaternionに変換

v=\begin{pmatrix} \lambda_x\\ \lambda_y\\ \lambda_z \end{pmatrix}

を回転ベクトルからQuaternionに変換する．

Q= \begin{pmatrix} \lambda_x sin\frac{\theta}{2}\\ \lambda_y sin\frac{\theta}{2}\\ \lambda_z sin\frac{\theta}{2}\\ cos\frac{\theta}{2} \end{pmatrix}

    /**
     * rvec->Quaternion変換
     *
     * @param rvec
     */
    private Quaternion RvecToQuaternion(double[] rvec) {
        double theta = Math.sqrt(rvec[0] * rvec[0] + rvec[1] * rvec[1] + rvec[2] * rvec[2]);
        double x = rvec[0] / theta * Math.sin(theta / 2);
        double y = rvec[1] / theta * Math.sin(theta / 2);
        double z = rvec[2] / theta * Math.sin(theta / 2);
        double w = Math.cos(theta / 2);
        return new Quaternion((float) x, (float) y, (float) z, (float) w);
    }

rvecをつかった制御

tvec,rvecというのはカメラからみた紙の位置，姿勢を表したVector3です．姿勢までも回転ベクトルで表されてしまっているので，これをクオータニオンに変更する必要があります．

紙の中心位置へと移動させる

撮影したカメラによってrvecの向きを補正

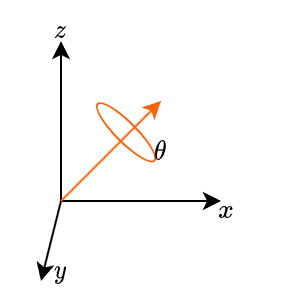
前方のカメラで撮ったのか，後方のカメラで撮ったのかによって取得したtvec,rvecの向きが異なります(あくまで画像から取得した値であるため)．以下の図を見ていただくとわかる通り，XYZ軸の向きが異なってることがわかります．(ちなみにこの図，深夜に混乱したときに頭の中整理するために書いた図です)

         double[] ar_nowcam_ASTROBEE_Pvec = new double[3];

         if (cameraType == RavensImageProcess.CameraType.NAV) {
             ar_nowcam_ASTROBEE_Pvec[0] = tvec[0];
             ar_nowcam_ASTROBEE_Pvec[1] = tvec[1];
             ar_nowcam_ASTROBEE_Pvec[2] = tvec[2];
             rvec[0] = rvec[0];
             rvec[1] = rvec[1];
             rvec[2] = rvec[2];
         } else {
             // DOCKカメラの場合は，上下以外が逆転している
             ar_nowcam_ASTROBEE_Pvec[0] = -tvec[0];
             ar_nowcam_ASTROBEE_Pvec[1] = -tvec[1];
             ar_nowcam_ASTROBEE_Pvec[2] = tvec[2];
             rvec[0] = -rvec[0];
             rvec[1] = -rvec[1];
             rvec[2] = rvec[2];
         }

rvecをQuaternionに変換

Quaternion ar_nowcam_ASTROBEE_Q = RvecToQuaternion(rvec);

ASTROBEEから見た紙の中心位置計算

ARマーカーから見た紙の中心を表すベクトルをQuaternionに変換

double[] papercenter_ar_AR_Vector4 = {paper_ar_PAPER_Pvec[0], paper_ar_PAPER_Pvec[1], paper_ar_PAPER_Pvec[2], 0};

$Q_1$ をrvec由来のar_nowcam_ASTROBEE_Q， $Q_2$ をpapercenter_ar_AR_Vector4とすると $Q_3=\overline{Q_1}Q_2Q_1$

Quaternion tmp = QuaternionMultiplication(new Quaternion((float) papercenter_ar_AR_Vector4[0], (float) papercenter_ar_AR_Vector4[1], (float) papercenter_ar_AR_Vector4[2], (float) papercenter_ar_AR_Vector4[3]), ar_nowcam_ASTROBEE_Q);
Quaternion tmp2 = QuaternionMultiplication(QuaternionConjugate(ar_nowcam_ASTROBEE_Q), tmp);
double[] papercenter_ar_ASTROBEE_Pvec = {tmp2.getX(), tmp2.getY(), tmp2.getZ()};//次元を3次に戻す(回転成分wは不要)

papercenter_ar_ASTROBEE_PvecがASTROBEEから見た紙の中心位置

撮影カメラに対するARマーカーの位置から、撮影カメラの取り付け位置を足してAstrobeeの姿勢に合わせて、ISS座標系でのARマーカーの位置を計算

ベクトルはスカラーじゃないからベクトル同士の足し算は問題ないです．．．(当たり前だけど，ぼーっとしてるとやらかしちゃったりします)

```
    double[][] astrobee_ISS_RM = quaternionToRotationMatrix(astrobee_ISS_Q);
    double[] ar_ISS_Pd = {astrobe_ISS_P.getX(), astrobe_ISS_P.getY(), astrobe_ISS_P.getZ()};
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            ar_ISS_Pd[i] += astrobee_ISS_RM[i][j] * (papercenter_ar_ASTROBEE_Pvec[j] + ar_nowcam_ASTROBEE_Pvec[j] + nowcam_astrobee_ASTROBEE_Pvec[j]);
        }
    }
```

この図を見て頂ければわかる通り，これらのベクトルの和とastrobeeの絶対座標の和が紙の中心の絶対座標になります．

ASTROBEEを回転させて紙の向きに合わせる(本番必要なかった)

今回の競技の得点ルールでは，紙の向きとAstrobeeを一致させる必要がなかったが，勘違いして作ったので一応載せておきます．

あと，なんで(0, 1, 0, 0),(1, 0, 0, 0)掛けるとうまくいくのかわからないままでした．

Quaternion papercenter_ASTROBEE_ISS_Q = QuaternionMultiplication(nowKinematics.getOrientation(), ar_nowcam_ASTROBEE_Q);
if (cameraType == RavensImageProcess.CameraType.NAV) {
    papercenter_ASTROBEE_ISS_Q = QuaternionMultiplication(papercenter_ASTROBEE_ISS_Q, new Quaternion(0, 1, 0, 0));
} else {
    papercenter_ASTROBEE_ISS_Q = QuaternionMultiplication(papercenter_ASTROBEE_ISS_Q, new Quaternion(1, 0, 0, 0));
}

謝辞

概要

実績