🎲

AtCoder Beginner Contenst 275 E 解答までの思考

2022/11/05に公開

競技プログラミング

AtCoder

tech

AtCoder Beginner Contest(ABC) 275のE問題について、
コンテスト中の考察の流れを書き残しておきます。

前提

筆者のレートは緑〜水をフラフラとしているくらいです。
想定解をスムーズに導くより、コンテスト中にどのような流れで解答に行きついたかの考えを
参考に残しているものです。

筆者がGo言語で競技プログラミングに参加しているため、サンプルのコードはGo言語で記載しています。

問題

下記のページからの引用です。

問題

問題文

高橋君は双六で遊んでいます。

この双六には $0$ から $N$ の番号がついた $N+1$ 個のマスがあります。高橋君はマス $0$ からスタートし、マス $N$ を目指します。

この双六では、 $1$ から $M$ までの $M$ 種類の目が等確率で出るルーレットを使います。高橋君はルーレットを回して出た目の数だけ進みます。もし、マス $N$ を超えて進むことになる場合、マス $N$ を超えた分だけ引き返します。

例えば、 $N=4$ で高橋君がマス $3$ にいるとき、ルーレットを回して出た目が $4$ の場合は、マス $4$ を $3+4-4=3$ マス超えてしまいます。そのため、 $3$ マスだけマス $4$ から引き返し、マス $1$ に移動します。

高橋君がマス $N$ に到達するとゴールとなり、双六を終了します。

高橋君がルーレットを $K$ 回まで回す時、ゴールできる確率を $\mod 998244353$ で求めてください。

確率 $\mod 998244353$ の定義
この問題で求める確率は必ず有理数になることが証明できます。また、この問題の制約下では、求める確率を既約分数 $frac{y}{x}$ で表したときに $x$ が $998244353$ で割り切れないことが保証されます。

このとき $xz≡y \pmod {998244353}$ を満たすような $0$ 以上 $998244352$ 以下の整数 $z$ が一意に定まります。この $z$ を答えてください。

制約

$M\leqN\leq1000$

$1\leqM\leq10$

$1\leqK\leq1000$

入力は全て整数

問題理解

まずは入力例1をもとに、 $mod$ を考えずに確率の問題としてシミュレーションしました。
ルーレットを $i$ 回 $(0\leqi\leqK)$ 回して、マス $j$ に到達する確率 $f(i, j)$ を考えます。

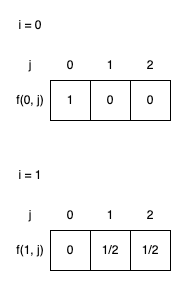
このような絵を描いて、問題文入力例1の「ゴールできる確率は $\frac{1}{2}$ です」ということは、 $f(0, 2)=0$ と $f(1, 2)=\frac{1}{2}$ の和と考えられました。

$f(i, j)$ をもう少し一般化しました。ルーレットを回して $x$ が出たときに $j$ に辿り着けるマスを $j'_{x}$ とするとこのような漸化式が組めてきました。

\begin{aligned} f(i, j) &= \frac{f(i-1, j'_{1})}{M} + \frac{f(i-1, j'_{2})}{M} + ... + \frac{f(i-1, j'_{M})}{M} \\ &= \frac{1}{M} \sum_{x=1}^M f(i-1, j'_{x}) \end{aligned}

さらに $0$ 回目での確率は決まっているので、まとめると下記のようになりました。

f(i, j) = \begin{cases} 1 \,\, &{i=0, j=0} \\ 0 \,\, &{i=0, 1 \leq j \leq N} \\ \frac{1}{M} \sum_{x=1}^M f(i-1, j'_{x}) \,\, &{1 \leq i \leq K} \end{cases}

漸化式から、この問題は動的計画法(DP)で解く方針で進めました。

DPの詳細検討

計算量の見積もり

漸化式をもとに、
$dp[i][j]$ ：ルーレットを $i$ 回まわして、マス $j$ に到達する確率
とします。計算量は $O(KNM)\leq10^7$ となる見込みで、実行時間制限内に計算できる見積もりが立ちました。
実際にコード化すると下記のようなループになる見込みでした。

main.go(DPに関するループ)

for i := 1; i <= k; i++ {
	for j := 0; j < n; j++ {
		for x := 1; x <= m; x++ {
			//ここにdp[i][j] += dp[i-1][j']のような処理を書いていく
		}
	}
}

フェルマーの小定理を適用する

DPを具体的にしていく段階で、確率を $\mod {998244353}$ で求めることを考えました。
漸化式の中で、 $frac{1}{M}$ の計算の仕方を変える必要があり、
これはAtCoderの過去問で学んだフェルマーの小定理を使用しました。
$p$ を素数として、 $a$ と $p$ が互いに素であるとき

a^{p-1} \equiv 1 \pmod p

が成立するという定理です。 $\frac{1}{M} = M^{-1}$ と考えると

M^{p-2} \equiv M^{-1} \pmod p

となり、 $M$ の累乗を代わりにかけていく道筋が立ちました。この計算は手元にライブラリ化していましたのでそれを使います。ここでは詳細を省略しますが、繰り返し二乗法を使って $O( \log p)$ 程度で計算できます。これはDPで用意する想定のループ内で毎回計算する必要もありませんので、予め計算しておけば前に見積もっておいた計算量が大きく変わることもありませんでした。

main.go(確率をmod 998244353で求めるための関数)

func Pow(x, y, p int) int {
	ret := 1
	for y > 0 {
		if y%2 == 1 {
			ret = ret * x % p
		}
		y >>= 1
		x = x * x % p
	}
	return ret
}

func Inv(x, p int) int {
	return Pow(x, p-2, p)
}

貰う、配るの再検討

次に $i$ 回目にマス $j$ にいるとき、 $i-1$ にどのマスにいるのかを計算しようとしましたが、ここで手が止まってしまいました。ここで $i$ 回目にマス $j$ にいて、 $i+1$ 回目にマス $j'_{x}$ に移動すると考え直しました。
問題の制約から、ルーレットで大きな数字が出ても、マス $N$ の近くのみを考慮すればよい(ルーレットで大きな数字が出て、マス $N$ から超えた分戻り、マス $0$ 分でまた折り返すことはない)ので、下記の計算で求められました。

j'_{x} = \begin{cases} 2N - (j + x) &\text{if} \,\, j + x > N \\ j + x &\text{otherwise} \end{cases}

これに合わせて、DPの書き方も漸化式通り貰うDPの書き方をしていたところを、配るDPの書き方に変更して下記のようにDPの遷移も書けてきました。

main.go(マスの移動と、DPの遷移)

dp[0][0] = 1
//pは別のところで998244353と定義
im := Inv(m, p)
//今jにいてルーレットでxが出た時、次の位置
computeNext := func(j, x int) int {
	if j+x > n {
		over := j + x - n
		return n - over
	} else {
		return j + x
	}
}
for i := 0; i < k; i++ {
	for j := 0; j < n; j++ {
		for x := 1; x <= m; x++ {
			next := computeNext(j, x)
			dp[i+1][next] += dp[i][j] * im
			dp[i+1][next] %= p
		}
	}
}

実装

ここまで書けたところで問題の入力例を試してみましたら、入力例2だけ想定の出力が得られませんでした。

実行例(入力例2)

$ go1.14.1 run main.go
10 5 6
453091133

これは解答として $dp[K][N]$ を出力していたためでした。
答えはルーレットを $K$ 回まで回す時、ゴールできる確率ですので、 $\sum_{i=1}^K dp[i][N]$ を出力しなければいけませんでした。

main.go(最後の解答を計算)

var ans int
for i := 1; i <= k; i++ {
	ans += dp[i][n]
	ans %= p
}
return ans

これを適用して入力例2も想定の出力が得られました。

実行例(入力例2、修正版)

$ go1.14.1 run main.go
10 5 6
184124175

最終的なACコードは下記のようになります。

main.go

package main

import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)

var sc = bufio.NewScanner(os.Stdin)
var out = bufio.NewWriter(os.Stdout)

func main() {
	buf := make([]byte, 1024*1024)
	sc.Buffer(buf, bufio.MaxScanTokenSize)
	sc.Split(bufio.ScanWords)

	n, m, k := nextInt(), nextInt(), nextInt()
	ans := solve(n, m, k)
	PrintInt(ans)
}

func solve(n, m, k int) int {
	const p = 998244353
	dp := make([][]int, k+1)
	for i := 0; i <= k; i++ {
		dp[i] = make([]int, n+1)
	}
	dp[0][0] = 1
	im := Inv(m, p)
	//今jにいてルーレットでxが出た時、次の位置
	computeNext := func(j, x int) int {
		if j+x > n {
			over := j + x - n
			return n - over
		} else {
			return j + x
		}
	}
	for i := 0; i < k; i++ {
		for j := 0; j < n; j++ {
			for x := 1; x <= m; x++ {
				next := computeNext(j, x)
				dp[i+1][next] += dp[i][j] * im
				dp[i+1][next] %= p
			}
		}
	}

	var ans int
	for i := 1; i <= k; i++ {
		ans += dp[i][n]
		ans %= p
	}
	return ans
}

func nextInt() int {
	sc.Scan()
	i, _ := strconv.Atoi(sc.Text())
	return i
}

func PrintInt(x int) {
	defer out.Flush()
	fmt.Fprintln(out, x)
}

func Pow(x, y, p int) int {
	ret := 1
	for y > 0 {
		if y%2 == 1 {
			ret = ret * x % p
		}
		y >>= 1
		x = x * x % p
	}
	return ret
}

func Inv(x, p int) int {
	return Pow(x, p-2, p)
}

最後に

今回解法に早く気がつけたのは、今年の夏頃に期待値を求める問題に苦手と感じることがあり、
確率、期待値に関して集中して学び直していたことがきっかけかもしれません。
苦手を感じたのが、まさに今回のSugoroku 4の前のナンバリング問題であるSugoroku 3でした。

楽しみながら、手を動かしながら学べたのが、書籍数学ガールや、アルゴ式のプログラミングで学ぶ数学のコンテンツでした。最後に参考に紹介させていただきます。
https://www.sbcr.jp/product/4815606039/
https://algo-method.com/courses/13