数式なし!やさしく学ぶ『効果検証』― 回帰分析・因果推論の各手法の違いがスッとわかる ―
はじめに
マーケティング施策やキャンペーン、機能改善を行った際に、「この取り組みは本当に効果があったのだろうか?」と考える場面があるかと思います。
本記事では、統計や因果推論に詳しくない方でも読みやすいように、数式を使わず、主要な効果検証の考え方や手法を整理しました。
内容に誤りなどありましたら、ぜひコメントで教えていただけると幸いです。
本記事の主な想定読者
- 施策実施を行っているが、効果を正しく評価できているか不明なビジネス担当者
- 統計を学び始めた初学者・学生
なぜ"正しい効果検証"が必要なのか
単純に Before(施策前)と After(施策後) の数字だけを比べただけでは「売上が伸びた=施策の効果があった」とは判断しきれない場面があります。
その理由として、季節要因・トレンドなどの外部要因や比較する対象(顧客層・期間など)の違いが影響している可能性があるためです。
こうした要因を考慮しないまま結論を出してしまうと、
・実際より良く見えてしまう(過大評価)
・逆に悪く見えてしまう(過小評価)
といった形で、結果を誤って解釈してしまうリスクがあります。
外部要因の例(施策とは無関係で数字を動かすもの)
| 外部要因 | 問題点 |
|---|---|
| 季節要因(夏休み・年末年始) | 自然に売上が上がり、施策の効果と勘違い |
| 競合の動き(値下げ・新商品) | 他社の施策が、自社の成果に見えてしまう |
| 市場全体のトレンド | 業界全体が伸びているだけの可能性 |
母集団の違いの例(比較している人や条件が違う)
| 比較のズレ | 問題点 |
|---|---|
| 施策前:既存ユーザー / 施策後:新規ユーザー中心 | “施策”ではなく“客層の違い”を見ているだけ |
| 施策前:全ユーザー / 施策後:高アクティブ層のみ | もともと離脱しにくい人だけを見てしまっている |
この影響を除いて"真の施策効果"を正しく評価するのが効果検証の取り組みになります。

こうしたズレによる本来の効果との誤差のことをバイアスと呼び、特に「比較する集団の性質が異なること」で生まれるバイアスをセレクションバイアス(選択バイアス) と呼びます
主な効果検証手法
これらの影響を除いた状態で"真の施策効果"を測るには、施策実施群、未実施群をそれぞれ「まったく同じサンプルで比較」するのが最も理想的な手法ですが、現実的に不可能です。
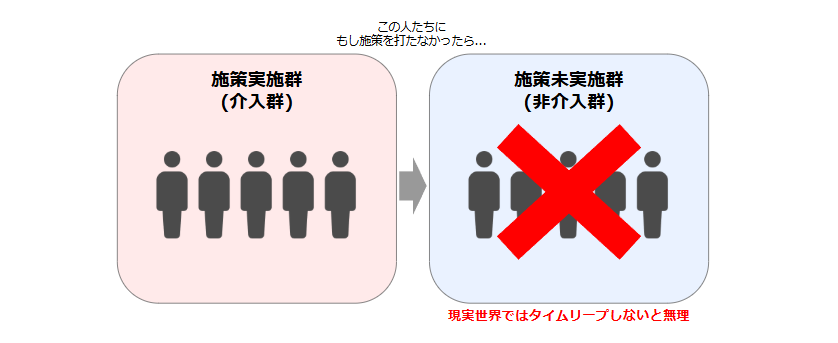
そこで、いくつかの対応方法が挙げられます。
・比較する母集団をそろえる:BeforeもAfterも「高アクティブ層のみ」に実施
・重みづけをする:全体に合わせた指標に補正して比較する
・コントロールグループを作る:施策対象層と非対象層を同じ属性で比較する
この対応方法を実現するいくつかの代表的な手法を紹介します。
ランダム化比較試験(RCT:Randomized Controlled Trial)
対象ユーザーをランダムに2グループに分け、片方に施策を実施して効果を比較する手法
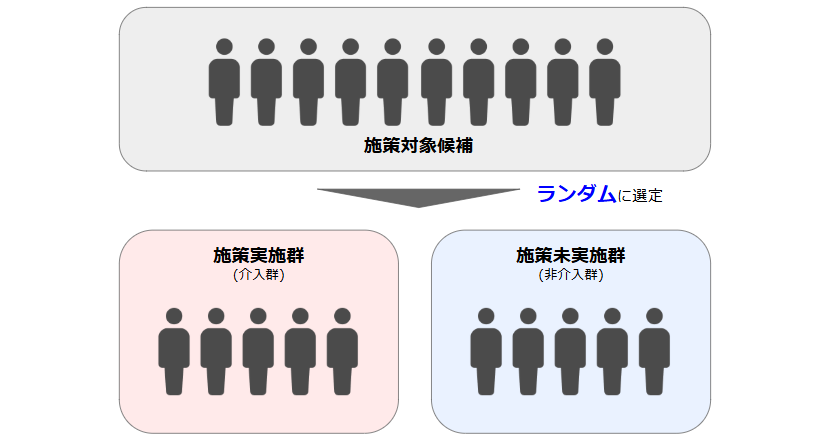
ビジネス例:
広告Aを半分のユーザーに表示、残りには広告Bを表示し、どちらが売上を伸ばすかを比較
メリット
- ランダムに分けることで、外部要因やユーザー属性の差が平均化されやすい
- 結果の解釈が直感的でわかりやすい
デメリット
- ランダムに分けるため、施策を意図的に届けられないユーザーが出る(機会損失やコストが発生)
- サンプル数が少ないと偏りが残る可能性がある
注意点
- 本当にランダムに分割できているかを事前に確認する
- サンプル数が十分にあるかを検討する
- 大きなイベントや外部要因が重なる期間は、結果が偶然に左右されることもある
回帰分析
他の条件(広告費・季節・顧客属性など)をそろえた上で、「施策を受けることで効果がどのくらい増えるか?」を推定する手法

ビジネス例:
広告費やキャンペーン期間、季節要因などを考慮したうえで、キャンペーン有無が売上に与える影響を測る
メリット
- 施策後に蓄積されたデータを使って効果を推定できる
- 属性の違いや外部要因を統計的に補正できる
デメリット
- モデルの前提(線形性、独立性など)が守られていない場合、結果が歪むことがある
- 考慮できていない交絡因子[1]があると完全には補正できない(=偏りが残る)
- モデルの範囲を超えた予測(未知のケース)には弱い
注意点
- モデルの前提(線形性・独立性など)を確認することが重要
- 結果を信頼性を担保するために、残差分析などのモデル診断を行う
- 施策に関係しそうな変数は、できるだけ漏れなく取り入れる
傾向スコアマッチング(PSM:Propensity Score Matching)
「施策を受けそうな確率(=傾向スコア[2])」をもとに、条件が似ているユーザー同士をペアにして比較する手法
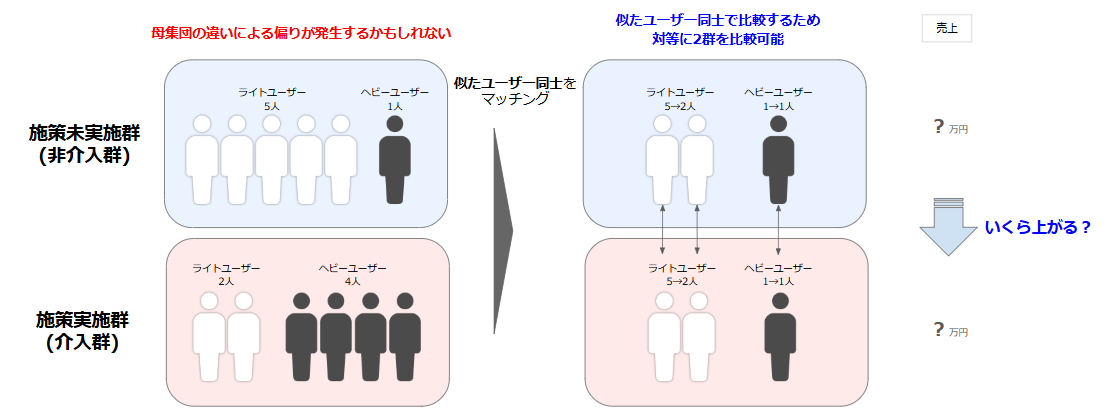
ビジネス例:
広告を見たユーザーと、属性や行動が近い広告未接触ユーザーをマッチングし、売上の差を比較
メリット
- 施策後に蓄積されたデータだけで効果を推定できる
- 属性の偏りを統計的に補正し、公平な比較がしやすい
- ペア比較なので、結果が直感的に理解しやすい
デメリット
- 条件が近いユーザーが少ないと、サンプルが減ることがある
- モデルに入れていない要因(未観測の交絡因子)は補正できない
注意点
- マッチング後、バランス(例:標準化差) が取れているか必ず確認する
- 重複や極端な値を含むユーザーには注意する
逆確率重み付け(IPW:Inverse Probability Weighting)
「施策を受けそうな確率(=傾向スコア)」の逆数を重みとして使い、偏りを補正することで「もし母集団全体が均等に施策を受けた/受けなかった場合の平均的効果」を推定する手法

※ 非実施群にも同様に補正をかけて補正後の実施群 ー 補正後の非実施群で効果を測る方法もある
ビジネス例:
広告を受けやすいユーザー/受けにくいユーザーの偏りを調整し、広告全体として「どれくらい売上に影響したか」を推定
メリット
- 施策後に蓄積されたデータだけで効果を推定できる
- 属性の偏りを統計的に補正可能
- サンプルを削らずに使える(PSMのようにマッチングで除外しない)
デメリット
- 施策を受ける確率が極端(0や1に近い)な場合、重みが大きくなり不安定
- モデルに入れていない要因(未観測の交絡因子)は補正できない
注意点
- 重みが極端になっていないか(外れ値)を確認する
- モデルの妥当性を確認する(バランス等)
差の差分法(DID:Difference In Differences)
施策前後の変化を施策を受けたグループと受けていないグループで比べる手法

ビジネス例:
キャンペーン前後で売上の変化を確認し、同時期にキャンペーンを行っていない店舗の変化と比べる
メリット
- 時間による変化や外部要因の影響をある程度補正して効果を推定できる
- 施策後に蓄積されたデータだけで効果を推定できる
デメリット
- 「施策がなければ両グループは同じように変化したはず」という前提(平行トレンド)が崩れると
結果が偏る - 複雑な非線形トレンドには対応しにくい
注意点
- 過去データで平行トレンドを確認する
- 他の施策や外部イベントの影響を考慮する
回帰不連続デザイン(RDD:Regression Discontinuity Design)
施策が適用される境界(スコアや年齢など)の直前・直後のデータを比べて、施策の効果を推定する手法

ビジネス例:
・得点が80点以上なら特典を付与 → 79点と80点を比較
・年齢が65歳以上なら割引開始 → 64歳と65歳を比較
メリット
- 境界付近では、ほぼランダムに近い条件で比較できる
- 施策後に蓄積されたデータだけで効果を推定できる
- 実務上の倫理的・運用上の制約が少ない
デメリット
- 境界付近のデータしか使えないため、サンプルが限られる
- 境界外の効果は推定できない
- データのノイズやバンド幅の設定によって結果が変わる
注意点
- 境界付近で不自然なジャンプがないか確認する
- 適切なバンド幅を選ぶ
- 必要に応じて局所回帰で他の条件(共変量)を補正する
実務での選び方の目安
各手法について、「どんな状況ならどの手法を検討すべきか」という視点で、選び方の目安を整理しました。
-
事前にA/Bテストとして設計できる場合 → RCT
最も信頼性が高い方法。意図的にグループを分けられる状況なら最優先。 -
既に施策を実施済で、過去データで評価したい場合 → 回帰分析 / PSM / IPW / DID / RDD
事前のグループ分けはできなかったが、実施済データを使って推定したいときの手法群。 -
施策対象と非対象で属性や行動が偏っている場合 → PSM / IPW / 回帰分析
「優良顧客だけ施策を受けた」など、個人属性によるバイアスを補正したい場合の方法。 -
時間による変化(季節・市場全体の影響)も考慮したい場合 → DID
キャンペーン前後で全体が変動するようなケース(季節要因や全体需給など)に有効。 -
年齢やスコアなど、明確な境界で施策対象が決まる場合 → RDD
年齢65歳以上、スコア80点以上に施策を適用など、閾値が存在するケースに有効。 -
個別ではなく「全体として効果があったか」を知りたい場合 → IPW / 回帰分析 / DID
マーケ施策全体の投資判断や、全体の平均効果を把握したいケースに有効。 -
店舗・地域など、グループ単位で施策した場合 → DID / 回帰分析
個人ベースではなく、エリアや店舗など集計単位で分析するときに有効。
Discussion