🎉
【論文紹介】MulLeak, TCHES2025.2, KYBERの乗算部分をSCAした論文

2025/03/11に公開
Security
 今回の論文Title: MulLeak: Exploiting Multiply InstructionLeakage to Attack the Stack-optimized KyberImplementation on Cortex-M4
Authors: University of Science and Technology of China, Hefei National Laboratory, Zhejiang Wanli University
Where: TCHES
Year: 2025
URL: https://tches.iacr.org/index.php/TCHES/article/view/12041/11885

 要約pqm4のstack-optimized実装をプロファイリング攻撃
stack-optimized実装はメモリアクセスが減るためリークが少ない。さらに1レジスタに2係数がパックされるため攻撃が難しくなる。
Cortex-M4の乗算命令をモデリングし、線形回帰ベースのプロファイリング攻撃を行った結果、unprotected実装は10数波形程度、1次マスク実装は200波形程度で攻撃できた。

 所感いわゆるテンプレート攻撃やDLと異なり、乗算命令をリバエンしてspecificな電力モデルを作っているところがおもしろい。
乗算命令をリバエンする部分は確かに面白いんだが、その部分のリークへの寄与は大きくないように見えるので、オペランドだけでやってもそれなりに性能出るんじゃないだろうか？
数十波形程度で攻撃できていてすごいと思うが、先行研究もCPAで200波形でできてるしこんなもんなんだろう。PQC弱くね？

 1. IntroductionKyberのspeed optimized実装とmemory optimized実装では攻撃手法が異なる。speed opt.のほうはlazy reductionのためにstore命令を多用しリークが多い。また係数ごとに攻撃できる。memory opt.は32bitレジスタに二つの係数を格納するため難しい。またstoreの回数も減る。
memory opt.のpqm4実装のmul命令に関して、cycle-levelのregressionで攻撃する。選択平文ならmask実装も攻撃可能？

 2.3 ARM Cortex-M4FE, DE, EXの3段パイプラインで、MUL含むほとんどの命令が1サイクル実行。WBステージはない。次の命令が前の命令の値を使う場合、フォワーディングネットワークを介して、パイプラインレジスタに格納される。つまり1サイクル命令はストールしない。load/store命令のような複数サイクル命令があるとストールする可能性がある。
割り込みや、分岐予測がない場合、あるサイクルにおけるFEとDEの電力は一定と仮定できる。この仮定によりあるサイクルの電力はEXの電力＋レジスタ更新の電力（ハミング距離）＋他になる（５式）
EXステージの消費電力は
パイプラインレジスタ：オペランドのハミング距離
結果：GPRに書き込まれる値もEXステージでフリップするので、destレジスタのハミング距離
命令：MUL命令の組み合わせ回路の電力
サイクルtの電力を次のようにモデル化して線形回帰する。
oはオペランド、\tilde{o}は直前の命令のオペランド、rは演算結果、\tilde{r}は前の命令の演算結果（というよりdestレジスタに入ってる値？）
簡単に言うと現在のオペランドと結果の値、それらが格納されるレジスタのハミング距離、そして演算中の値DM,とその遷移TDMである。

 3.2リバエンしてMUL回路の構成を推測する。基本的には、radix-2 Boothか、radix-4 Boothか、Baugh-Wooley法かを見分ける。radix-2ならnビット乗算に対してn部分積が出てくる。radix-4ならその半分になる。Baugh-Wooleyは対称的なので対象分布になる？
0\times HW(1)とHW(1) \times 0のデータセットを計算する。
図4より、乗数と被乗数の影響が対象じゃなさそうなのでBaugh-Wooleyじゃなさそう。またmultiplicandのほうが電力が大きいので、こっちでBooth encodeしてそう。radix-2だとすべてのケースで負数になるはずで、負数はたくさんフリップするので電力が多くなる。しかし電力は奇数のみ電力が高いので、これはradix-4のケースだと推測した。
典型的なradix-4 Booth乗算器を実装し、その部分積などの中間値を


としてモデルに組み込む。

 3.4提案モデルをより実際のリークに近づけるように調整。攻撃対象のコードに使われているsmu系の命令は16x16ビット乗算を2並列実行する。これをモデル化。ほか、使って無いビットを排除したりいろいろ調整する。

 4. 提案手法doublebasemul_frombytes_asmを攻撃する。これはレジスタpoly0にパックされた二つの係数と、レジスタpoly1にパックされた二つの秘密鍵を1次式として乗算（モンゴメリリダクション）するもの。
smulttはレジスタの上位16ビットを乗算する命令で、ここで\hat{ct_1} \times \hat{sk_1}が計算される。5，6行目でモンゴメリリダクションして、7行目でzeta乗算。8行目smlabbで\hat{ct_0} \times \hat{sk_0}をアキュムレートし、9，10行目でリダクションして\hat{r_1}を得る。同様に\hat{r_0}を計算して14行目で結果を一つのレジスタにパック。最後にメモリにストアする。

 4.2 Known Ciphertext Profield Attackasmの上4行目は\hat{sk_1}のみに依存するので、まずそれから当てる。\hat{ct_1}=0の暗号文はリークが変わるので破棄する。
4オペランドでリークをモデル化（\hat{sk_0}=0）し、
残差から尤度を求め、鍵ランクとする。
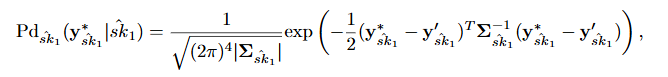
\hat{sk_1}については、推測した\hat{sk_0}を使って、同じように4～9行目のリークで攻撃。

 4.3 Chosen Ciphertext Profield Attack選択暗号文を使うことで、\hat{sk_1}と\hat{sk_0}を独立に攻撃できる。
特に\hat{ct_0}=0とするのが有効？（本文と図に書いてあることが違う気がするけどたぶんこういうことだと思う）

 4.4 The Second-order Chosen Ciphertext Profield AttackNTTは線形なのでマスキング実装では独立に動いてるだけ。4.3の手法を単純に結合して使う。すなわち、ある秘密鍵シェアのNTT波形が
のように与えられたとき、それぞれの鍵シェアの尤度を4.3と同じやり方で求められる（鍵は固定値なので求められるが、シェアは毎回変わるので求められるのか？計算はできるか。）。
ある鍵の尤度を、この対数尤度の和で定義する。
これでできそうだが、鍵候補が指数的に増加し、複雑になるため効率化のために枝狩りを導入する。各シェアの尤度に閾値を導入し、ある閾値以下のものは計算しない。

 4.5 Assistance with the Store Instruction
最後に係数パックレジスタをストアする部分のリークは強いので、この部分はテンプレート攻撃して、秘密鍵候補をvalidateする。ハミング重みしか漏れないので大したことはできないが多少効率に寄与する？

 5. Experiments and Resultsプロファイルとターゲットは一応違うデバイスでやってる？
NTT乗算の中にdoublebasemul_frombytes_asmマクロが64回現れるので、これを64個に分けてプロファイルする。つまり1波形で64個分プロファイルできる。
まずロード命令の場所を特定する。ct_0||ct_1のハミング重みがロードで漏れるので、ランダムに生成したct_0, ct_1を23のHWグループに分け（0以外？）、それぞれのグループで100暗号文作る。この暗号文と、all-zero秘密鍵を入力して波形を取得する。
各サンプル点でSoST(sum-of-squared t-values)を計算して、ピークを見る。ロード命令はEXステージの後にロードが行われるので、そこでピークになるのが特徴である。各命令の後に3NOP追加して、命令とリークの位置を関連付けた。

 5.21サイクルの消費電力を和として1点に圧縮する。→cycle-level power consumption（目的変数）
消費電力モデル（説明変数）をF検定して不要な変数を削除？
cycle-level power consumptionと説明変数を回帰分析
決定係数でプロファイリング波形数の影響を見たところ、32000プロファイル（500波形）くらいでほぼフィットする。
また表9で各説明変数の寄与度を見たところ、DMとTDM（組み合わせ回路リーク）は有意水準を超えており、攻撃に使えることがわかる。有意水準を超えてないところはモデルからはずす。

 5.3重要じゃなさそうなので省略。
ストア命令のリークによる補正方法がかかれている

 5.4 Attack and Performance5.4.1 The First-order Attacks
表6に結果がまとめられている。一番結果がよかったのはOriginalの既知暗号文攻撃で、12波形で攻撃可能（SR>99.99）。ストア命令のリークによる補正は想像通りというかあまり意味ない。SRの増加でみるとCondを使ったほうが若干よくなっているのがわかる。一方で選択暗号文だとCond2を使ったほうがよくなっている。
選択暗号文のほうが悪い結果なのは意外だが、CCPAだと\hat{sk_0}のリークが2命令だけになるので妥当といえば妥当。
今回のケースではプロファイリング波形数の影響は大きくなかった。
これでKyber-768の全秘密鍵係数をあてようとすると97%くらいのSRになる（どういう計算？0.9999^{384}?）
5.4.2 The Second-order Attacks
CCPAで2～300波形で攻撃できた。KCPAはsk_0の回復にsk_0が必要なので難しいのでやらない。
ランクの低いものは計算しない閾値th_{rank}と、Cond1に使うハミング重みn_{hw}のパラメータがある。基本的に\hat{sk_0}のリークが少ないためそっちのほうが難しい。Cond1を使うと\hat{sk_1}は悪くなるが\hat{sk_0}がよくなるので全体としてよくなる。n_{hw}=1が一番良かった。
th_{rank}の影響はそれほど大きくないが、結果としては512が一番良く、Cond1と併用した場合201波形でSR=99.99%に達する。

 5.5 Comparison[MWK+24]はCPAしてるだけという感じの手法で、200波形で破れている。non-profiling
[ABB+24]は大量の波形で正確なテンプレートを作り、single trace attackする。SRの値は鍵多項式全体に対するものだと思われるがあってるか？また参照デバイスと攻撃デバイスを同じでやってるのが大きな違い。
選択暗号文という観点では？

 6 DiscussionLR-based Leakage Model
従来のSCAの線形回帰式3は、ある時刻のリークを回帰しているが、今回のもの（式１に近い）は、命令単位で学習するので精度が上がる？式３は式１の一般化である的なことだと思うけどよくわからない。
Noise
STM32はSNRが良いので攻撃しやすい。SNの影響を見るため波形にノイズを加えて実験？ノイズを増やしても1000波形以下でできるっぽいが、マスク実装だと1000だと厳しい。図に何をプロットしているかいまいちわからない。SR=99.99%の点？だとしたら図15と対応取れなくないか？
Application to Plantard Implementation
pqm4にはPlandard版の実装も取り込まれている。ここでは９乗算命令が使われており、本論文より１つ少なくなるため、わずかにリークが減る。また符号付乗算や32x32乗算を使用しているため、わずかにリークモデルが異なる。とはいえできそう。